线性代数学习笔记(十二)
2016-09-13 01:42
211 查看
即使是实数矩阵,其特征值也可能为复数。所以我们也需要考虑矩阵元素为复数的情况。
以下各小节可概括为一句话:将复数向量/矩阵转置时,记得同时对其取共轭!
假如向量z=[z1 z2 ... zn]T, 每个分量都可能是复数,那么∥z∥2∥z∥2 就不再是zTz,而是z¯Tzz¯Tz。
“共轭再转置”有个简化标记:z¯T=zHz¯T=zH,H表示Hermitian
Review:在复平面上理解复数a和复数b相乘,结果的模长是a和b模长的乘积,结果的角度是a和b角度之和。当a与b共轭时,角度正好为2pi。
和模长类似,向量y 与 向量x 的内积=y¯Tx=yHxy¯Tx=yHx
Note:内积的结果有可能是复数(但模长只能为实数)。
为什么要定义对称复数矩阵?我们希望对称矩阵的特性(1.特征值都是实数;2. 特征向量互相垂直)在复数矩阵上也成立。
在证明对称矩阵的特征值都是实数时,关键一步是:x¯TAx=x¯Tλx=x¯TA¯Txx¯TAx=x¯Tλx=x¯TA¯Tx(参见上一节笔记),我们需要 A=A¯T=AHA=A¯T=AH才能保证复数矩阵特征值依然为实数。
因此,复数矩阵的对称性:A=A¯T=AHA=A¯T=AH,可知主对角线必为实数,且对称元素共轭。这和直观感觉的不是很一样,比如下面这个复数矩阵是对称的(感受一下):
[23+3i3−3i5][23−3i3+3i5]
实对称矩阵的特征向量相互垂直,将所有单位特征向量按列向量拼凑,得到正交矩阵Q,有:QTQ=IQTQ=I
复对称矩阵的(复数)特征向量也相互垂直,其单位特征向量组成的正交矩阵(称之为酉矩阵)Q,有:Q¯TQ=QHQ=IQ¯TQ=QHQ=I
PS:第一次见到“酉”这么奇怪的翻译,百度为什么这么翻译得到的结果是:“酉”是Unitary的音译,据说是华罗庚的建议。中英文都有“一”和“元”的意思。
形式见下,并且满足:
wN=1wN=1,也就是:

是1的

次方根的主值(primitive
nth root of unity),大小为
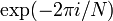
,这里这个负号是依据惯例加的
将矩阵除以根号下N是依据惯例而加,目的是将列向量的模长变成1,从而成为单位正交基

这个矩阵在传统意义上对称,但不是Hermitian对称(1.主对角线元素不是实数;2.共轭转置不等于原矩阵)。
但是,这个矩阵是酉矩阵(unitary matrix),其不同列的列向量内积=0,也就是WHW=I(待解决:为什么W的列向量是一组正交基?)
由上可知,WT=WH,也就是 傅里叶逆矩阵 同样具有 傅里叶矩阵 的性质(什么性质?似乎就是:1. 列是基;2. 可用FFT)
我们需要将F或者F-1与向量相乘,常规方法需要n2次乘法,FFT利用矩阵的周期性,将复杂度降为O(n*log n),这个方法加速了众多工业领域的运算。
FFT的关键在于下面这个分解:

这部分讲的比较简略,没涉及到具体的例子,理解复杂度和应用还需要深入进去。BTW傅里叶变换在网易上也有一门专门的公开课。
复数
以下各小节可概括为一句话:将复数向量/矩阵转置时,记得同时对其取共轭!
向量的模长平方
假如向量z=[z1 z2 ... zn]T, 每个分量都可能是复数,那么∥z∥2∥z∥2 就不再是zTz,而是z¯Tzz¯Tz。“共轭再转置”有个简化标记:z¯T=zHz¯T=zH,H表示Hermitian
Review:在复平面上理解复数a和复数b相乘,结果的模长是a和b模长的乘积,结果的角度是a和b角度之和。当a与b共轭时,角度正好为2pi。
向量的内积
和模长类似,向量y 与 向量x 的内积=y¯Tx=yHxy¯Tx=yHxNote:内积的结果有可能是复数(但模长只能为实数)。
复数矩阵的对称性
为什么要定义对称复数矩阵?我们希望对称矩阵的特性(1.特征值都是实数;2. 特征向量互相垂直)在复数矩阵上也成立。在证明对称矩阵的特征值都是实数时,关键一步是:x¯TAx=x¯Tλx=x¯TA¯Txx¯TAx=x¯Tλx=x¯TA¯Tx(参见上一节笔记),我们需要 A=A¯T=AHA=A¯T=AH才能保证复数矩阵特征值依然为实数。
因此,复数矩阵的对称性:A=A¯T=AHA=A¯T=AH,可知主对角线必为实数,且对称元素共轭。这和直观感觉的不是很一样,比如下面这个复数矩阵是对称的(感受一下):
[23+3i3−3i5][23−3i3+3i5]
酉矩阵(Unitary Matrix)
实对称矩阵的特征向量相互垂直,将所有单位特征向量按列向量拼凑,得到正交矩阵Q,有:QTQ=IQTQ=I复对称矩阵的(复数)特征向量也相互垂直,其单位特征向量组成的正交矩阵(称之为酉矩阵)Q,有:Q¯TQ=QHQ=IQ¯TQ=QHQ=I
PS:第一次见到“酉”这么奇怪的翻译,百度为什么这么翻译得到的结果是:“酉”是Unitary的音译,据说是华罗庚的建议。中英文都有“一”和“元”的意思。
傅里叶变换
傅里叶矩阵
形式见下,并且满足:wN=1wN=1,也就是:

是1的

次方根的主值(primitive
nth root of unity),大小为
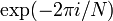
,这里这个负号是依据惯例加的
将矩阵除以根号下N是依据惯例而加,目的是将列向量的模长变成1,从而成为单位正交基

这个矩阵在传统意义上对称,但不是Hermitian对称(1.主对角线元素不是实数;2.共轭转置不等于原矩阵)。
但是,这个矩阵是酉矩阵(unitary matrix),其不同列的列向量内积=0,也就是WHW=I(待解决:为什么W的列向量是一组正交基?)
由上可知,WT=WH,也就是 傅里叶逆矩阵 同样具有 傅里叶矩阵 的性质(什么性质?似乎就是:1. 列是基;2. 可用FFT)
快速傅里叶变换(Fast Fourier Transform)
我们需要将F或者F-1与向量相乘,常规方法需要n2次乘法,FFT利用矩阵的周期性,将复杂度降为O(n*log n),这个方法加速了众多工业领域的运算。FFT的关键在于下面这个分解:

这部分讲的比较简略,没涉及到具体的例子,理解复杂度和应用还需要深入进去。BTW傅里叶变换在网易上也有一门专门的公开课。
