2015编程之美 骨牌覆盖问题·二 (快速幂)

描述

上一周我们研究了2xN的骨牌问题，这一周我们不妨加大一下难度，研究一下3xN的骨牌问题？所以我们的题目是：对于3xN的棋盘，使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢？首先我们可以肯定，奇数长度一定是没有办法覆盖的；对于偶数长度，比如2，4，我们有下面几种覆盖方式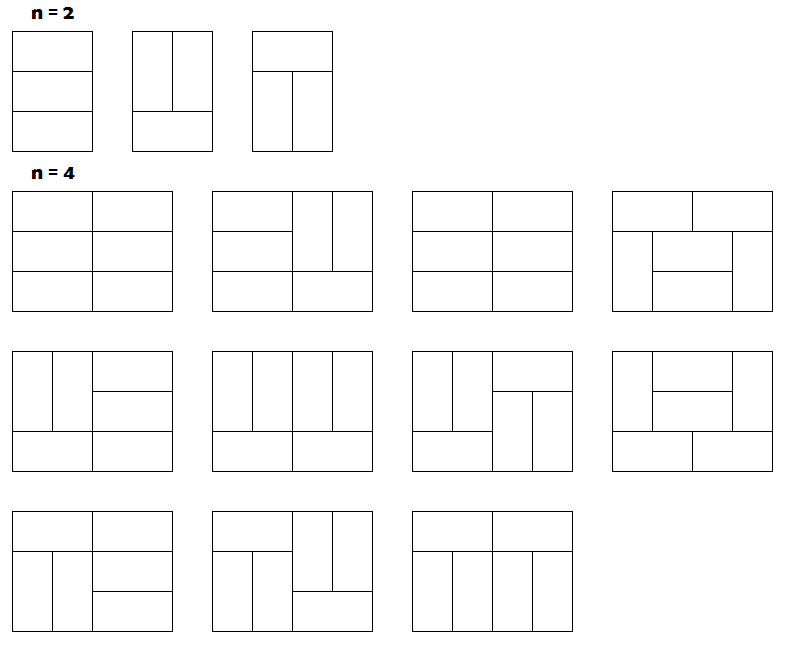：提示：3xN骨牌覆盖

输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 12357样例输入

62247088

样例输出

4037

提示：3xN骨牌覆盖
在2xN的骨牌覆盖问题中，我们有递推式子 (0,1)xM^n=(f[n-1],f
)。
我们考虑能否在3xN的情况下找到同样的式子。
但在实际的推导过程可以发现，对于3xN的覆盖，对应的f数值公式比2xN复杂太多。我们需要换个角度来思考推导公式。
在我们放置骨牌的过程中，一定是放好一行之后再放置下一行。根据摆放的方式，可能会产生很多种不同的形状，而这些形状之间是否具有某些递推关系呢？
如果他们存在一定的递推关系，则我们可以根据第i行的方案数来推导第i+1行的方案数。这样一行一行推导，直到第N行时不就得到了我们要求的方案数了么？
那么来研究一下是否存在这样的推导公式吧

假设我们已经放好了一些骨牌，对于当前最后一列(第i列)骨牌，可能有8种情况：



对于上面这8种状态，我们用数字来标记它们。以有放置骨牌的格子为1，未放置为0，转化为2进制数
以最下面一行作为1，则有：



接下来考虑如何放置骨牌，我们先将棋盘旋转一下。假设我们正在放置第i行的骨牌，那么会有下面3种方式：



灰色表示已经有的骨牌，绿色表示新放置的骨牌。
每一种放置方法解释如下，假设当第i行的状态为x，第i-1行的状态为y：第i行不放置，则前一行必须有放置的骨牌。x对应二进制位为0，y对应二进制位为1。
第i行竖放骨牌，则前一行必须为空。x对应二进制位为1，y对应二进制位为0。
第i行横向骨牌，则前一行必须两个位置均有骨牌，否则会产生空位。x对应二进制位为1，y对应二进制位为1。
举个例子：



对于第i行状态1，我们在第i+1行竖放两块骨牌之后便能到达状态6。
但是在这之中需要注意会出现下面这种情况：



这种情况看似是从状态1变成了状态0，其实是不对的。它不满足我们约定的放置方法，本质是第i行的状态1变成了第i行的状态7，而实际上我们应该放置的是第i+1行。
所以在枚举递推关系的时候一定要注意。
通过枚举8种状态到8种状态的转移，我们可以得到一个8x8的矩阵M（空白的地方均为0）：



m[i][j]表示从状态i变成状态j的方案数。

现在我们有了M矩阵，接下来考虑边界情况。
在2xN的骨牌覆盖中，有(0, 1)作为初始向量A，那么在3xN中初始向量A是如何呢？
让我们先想想A向量所代表的含义。M矩阵表示状态到状态的转移，则A向量所表示的应该就是第0行各状态的方案数。
同理，对于A * M^n所求出的结果则应该表示为第n行各种状态的方案数。
那么A向量应该是多少呢？很显然，第0行在我们递推的过程中必须看作状态7才合理。故A向量表示为：
{0, 0, 0, 0, 0, 0, 0, 1}
而对于我们寻求的答案，自然也是第n行放置为状态7的方案数了。

这个是网上别人做的，但是他的用时肯定比我们用快速幂大，其思想如下
其实仔细想想画一画也可以得到递推公式，假设奇数的方案数不为0，只要有一个方块达到奇数长度，就算是其中一个方案，那么有：a[0] = 0; a[1] = 2; a[2] = 3;对于奇数：a[i] = 2*a[i-1] + a[i-2];  对于偶数：a[i] = 3*a[i-2] + a[i-3];

#include <iostream>using namespace std;const long long mod=12357;long long N,A[5];void solve(){ A[0]=0;A[1]=2;A[2]=3; for(long long i=3;i<=N;i++) { if(i&1) A[i%5]=(2*A[(i-1+5)%5]+A[(i-2+5)%5])%mod; else A[i%5]=(3*A[(i-2+5)%5]+A[(i-3+5)%5])%mod; } cout<<A[N%5]<<endl;}int main(){ while(cin>>N) { if(N&1) cout<<"0"<<endl; else solve(); } return 0;}

这是我用快速幂的代码

#include <iostream>

#include <string.h>using namespace std;const long long mod=12357;struct node{    long long m[8][8];};node mul(node A,node B){    node C;    memset(C.m,0,sizeof(C.m));    for(int i=0;i<8;i++)        for(int j=0;j<8;j++)          for(int k=0;k<8;k++)            C.m[i][j]+=((A.m[i][k]%mod)*(B.m[k][j]%mod))%mod;    return C;}node pow(node M,long long N){    node res;    memset(res.m,0,sizeof(res.m));    for(int i=0;i<8;i++)        res.m[i][i]=1;    while(N)    {        if(N&1)            res=mul(res,M);        M=mul(M,M);        N/=2;    }    return res;}int main(){    long long N;    while(cin>>N)    {        if(N&1)        {            cout<<"0"<<endl;            continue;        }        node A,M;        memset(A.m,0,sizeof(A.m));        memset(M.m,0,sizeof(M.m));        A.m[0][7]=1;        for(int i=0;i<8;i++)            M.m[i][7-i]=1;        M.m[3][7]=M.m[6][7]=M.m[7][3]=M.m[7][6]=1;        node ans;        memset(ans.m,0,sizeof(ans.m));        ans=pow(M,N);        ans=mul(A,ans);        cout<<ans.m[0][7]%mod<<endl;    }    return 0;}