快速矩阵幂 hihoCoder1162 骨牌覆盖问题·三
2015-07-30 00:31
274 查看
相对于前两题,,前两题的矩阵可以手动构造出来,但是这题的矩阵就必须要自己完成了,因为实在是太大了
但是这个矩阵构造的方法,实在是巧妙~也是轮廓线dp的一个基础
按照它上面的提示,那个DFS就是枚举出所有的情况
让我们再回头看看我们上一期提示里面放置骨牌的约定:
假设我们正在放置第i行的骨牌,那么会有下面3种方式:
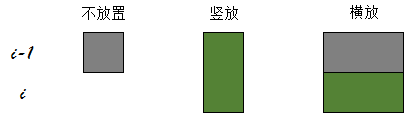
灰色表示已经有的骨牌,绿色表示新放置的骨牌。
每一种放置方法解释如下,假设当第i行的状态为x,第i-1行的状态为y:
第i行不放置,则前一行必须有放置的骨牌。x对应二进制位为0,y对应二进制位为1。
第i行竖放骨牌,则前一行必须为空。x对应二进制位为1,y对应二进制位为0。
第i行横向骨牌,则前一行必须两个位置均有骨牌,否则会产生空位。x对应二进制位为1,y对应二进制位为1。
既然有对应的二进制描述,那么上面三种方法就可以用程序语言解释为:
第i行不放置:new_x = x << 1, new_y = (y << 1) + 1; 列数+1
第i行竖放骨牌:new_x = (x << 1) + 1, new_y = y << 1; 列数+1
第i行横向骨牌:new x = (x << 2) + 3, new_y = (y << 2) + 3; 列数+2
通过迭代去枚举3种放置方法,当总的列数等于K时,此时的x便可由y转移过来。那么我们可以得到枚举放置的伪代码:
刚开始我一直没看清它的摆放顺序,那个长度为K的边在上下,长度为N的边在左右
所以每一行就是一个状态,然后开始枚举所有的状态,构造转移方程
刚开始我手推K=3的方程时候还差点推错了Orz,这个DFS感觉写的非常精辟而且很有用,大概思路也就是每一步都枚举出所有的可能情况。仔细看下还是能看懂的
顺便贴一个快速矩阵幂的好模板
但是这个矩阵构造的方法,实在是巧妙~也是轮廓线dp的一个基础
按照它上面的提示,那个DFS就是枚举出所有的情况
让我们再回头看看我们上一期提示里面放置骨牌的约定:
假设我们正在放置第i行的骨牌,那么会有下面3种方式:

灰色表示已经有的骨牌,绿色表示新放置的骨牌。
每一种放置方法解释如下,假设当第i行的状态为x,第i-1行的状态为y:
第i行不放置,则前一行必须有放置的骨牌。x对应二进制位为0,y对应二进制位为1。
第i行竖放骨牌,则前一行必须为空。x对应二进制位为1,y对应二进制位为0。
第i行横向骨牌,则前一行必须两个位置均有骨牌,否则会产生空位。x对应二进制位为1,y对应二进制位为1。
既然有对应的二进制描述,那么上面三种方法就可以用程序语言解释为:
第i行不放置:new_x = x << 1, new_y = (y << 1) + 1; 列数+1
第i行竖放骨牌:new_x = (x << 1) + 1, new_y = y << 1; 列数+1
第i行横向骨牌:new x = (x << 2) + 3, new_y = (y << 2) + 3; 列数+2
通过迭代去枚举3种放置方法,当总的列数等于K时,此时的x便可由y转移过来。那么我们可以得到枚举放置的伪代码:
DFS(x, y, col): If col == K d[y][x] = 1 Return ; End DFS(x << 1, (y << 1) + 1, col + 1); DFS((x << 1) + 1, y << 1, col + 1); If col + 2 <= K DFS( (x << 2) + 3, (y << 2) + 3, col + 2 ) End
刚开始我一直没看清它的摆放顺序,那个长度为K的边在上下,长度为N的边在左右
所以每一行就是一个状态,然后开始枚举所有的状态,构造转移方程
刚开始我手推K=3的方程时候还差点推错了Orz,这个DFS感觉写的非常精辟而且很有用,大概思路也就是每一步都枚举出所有的可能情况。仔细看下还是能看懂的
顺便贴一个快速矩阵幂的好模板
#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
#include<functional>
#include<algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int matMX = 130 + 5;
const int MX = 200000 + 5;
const int INF = 0x3f3f3f3f;
const int mod = 12357;
LL power(LL a, LL b) {
LL ret = 1;
while(b) {
if(b & 1) ret = ret * a % mod;
a = a * a % mod;
b >>= 1;
}
return ret;
}
struct Mat {
int m, n;
LL S[matMX][matMX];
Mat(int a, int b) {
m = a;
n = b;
memset(S, 0, sizeof(S));
}
Mat(int a, int b, LL w[][matMX]) {
m = a;
n = b;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
S[i][j] = w[i][j];
}
}
}
};
Mat mat_mul(Mat A, Mat B) {
Mat C(A.m, B.n);
for(int i = 0; i < A.m; i++) {
for(int j = 0; j < B.n; j++) {
for(int k = 0; k < A.n; k++) {
C.S[i][j] = (C.S[i][j] + A.S[i][k] * B.S[k][j]) % mod;
}
}
}
return C;
}
Mat Blank(int m, int n) {
Mat ret(m, n);
for(int i = 0; i < m; i++) {
ret.S[i][i] = 1;
}
return ret;
}
Mat mat_pow(Mat A, LL b) {
Mat ret = Blank(A.m, A.n);
while(b) {
if(b & 1) ret = mat_mul(ret, A);
A = mat_mul(A, A);
b >>= 1;
}
return ret;
}
LL T1[matMX][matMX], T2[matMX][matMX];
void DFS(int x, int y, int col, int k) {
if(col == k) {
T1[y][x] = 1;
return;
}
DFS(x << 1, (y << 1) + 1, col + 1, k);
DFS((x << 1) + 1, y << 1, col + 1, k);
if(col + 2 <= k) {
DFS((x << 2) + 3, (y << 2) + 3, col + 2, k);
}
}
int solve(int m, int n) {
memset(T1, 0, sizeof(T1));
memset(T2, 0, sizeof(T2));
int tot = 1 << m;
DFS(0, 0, 0, m);
/*for(int i = 0; i < tot; i++) {
for(int j = 0; j < tot; j++) {
printf("%d ", T1[i][j]);
}
printf("\n");
}*/
T2[tot - 1][0] = 1;
Mat A(tot, tot, T1), B(tot, 1, T2);
Mat ret = mat_mul(mat_pow(A, n), B);
return ret.S[tot - 1][0];
}
int main() {
int m, n;
//freopen("input.txt", "r", stdin);
while(~scanf("%d%d", &m, &n)) {
printf("%d\n", solve(m, n));
}
return 0;
}
相关文章推荐
- 您还有心跳吗?超时机制分析(java)
- 安装windwos10 SDK RTM
- display 与 visible 属性比较
- 【HDU3466】【Proud Merchants】
- 《一起学》系列10:Nginx入门
- uva--1368(贪心,字符串模拟)
- 系列10:Nginx入门
- [第1章]地图:iOS模拟器的使用
- gdb 条件断点
- 《一起学》系列9:Linux & shell
- gdb 调试宏
- 系列9:Linux内核
- 如何管理 Vim 插件
- Quartus “Error: Project too complex: hierarchy path is too long ”的解决办法
- 《一起学》系列8:网络编程
- 系列8:网络编程
- 点评版:函数源代码 strcpy/memcpy/atoi/kmp/quicksort
- 7种形式的Android Dialog使用举例
- C#与.NET概述
- 2015-07-29
