李宏毅机器学习——逻辑回归
逻辑回归
第一步先选择函数集
步骤一:函数集
接上一篇,我们知道,给定一个x,它属于类别C1C_1C1的概率为Pw,b(C1∣x)P_{w,b}(C_1|x)Pw,b(C1∣x),
如果Pw,b(C1∣x)≥0.5P_{w,b}(C_1|x)\geq0.5Pw,b(C1∣x)≥0.5则属于C1C_1C1;否则属于C2C_2C2
最后我们得到
Pw,b(C1∣x)=σ(z),σ(z)=11+exp(−z)P_{w,b}(C_1|x) = \sigma(z),\quad \sigma(z)=\frac{1}{1+exp(-z)}Pw,b(C1∣x)=σ(z),σ(z)=1+exp(−z)1
z=w⋅x+b=∑iwixi+b
z = w \cdot x + b = \sum_i w_ix_i + b
z=w⋅x+b=i∑wixi+b
所以我们的函数集是fw,b(x)=Pw,b(C1∣x)f_{w,b}(x) = P_{w,b}(C_1|x)fw,b(x)=Pw,b(C1∣x),包含所有不同的www和bbb。
图形化表示如下:
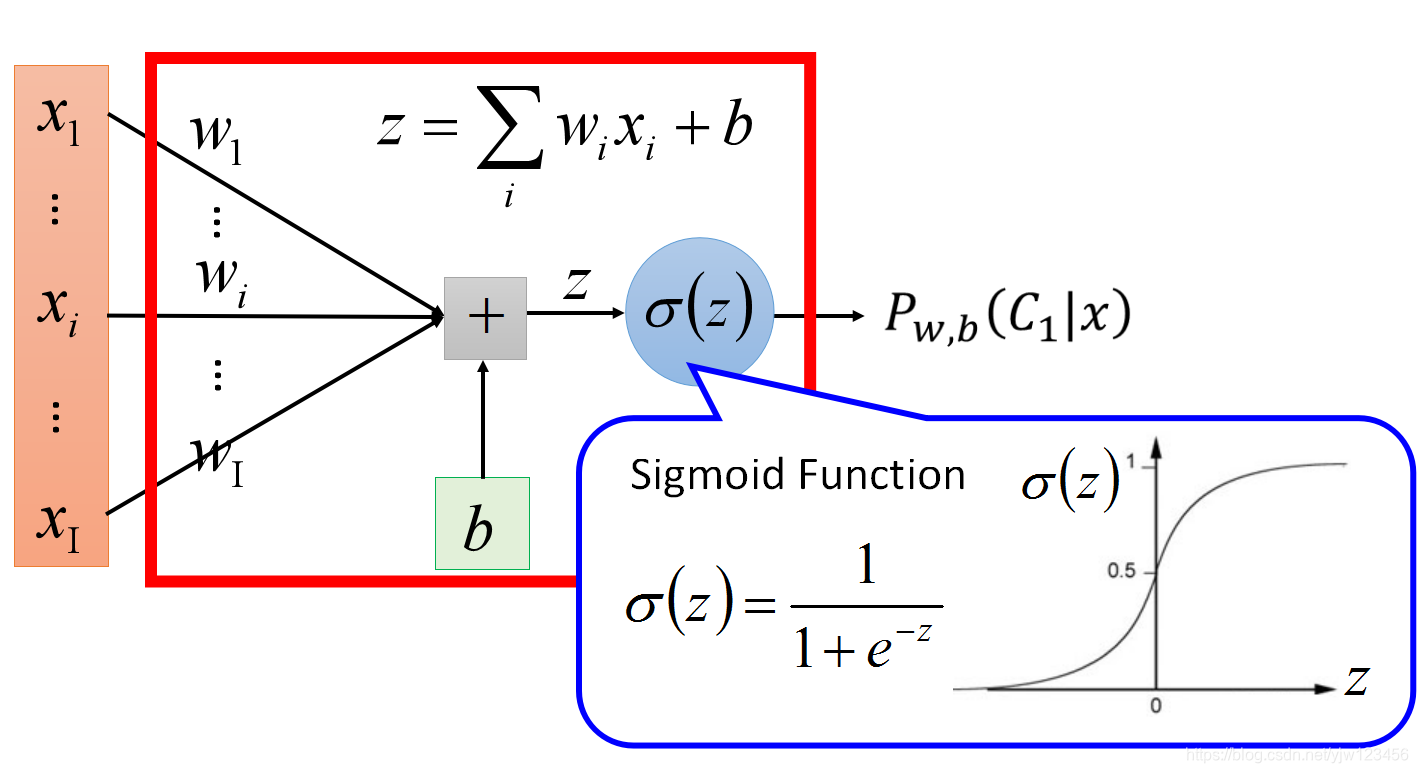
这个就是逻辑回归,我们与线性回归做一个比较。

因为Sigmoid函数的取值范围是0到1,因此逻辑回归的输出也是0到1;而线性回归的输出可以是任何值。
接下来判断函数的好坏
步骤2: 函数有多好
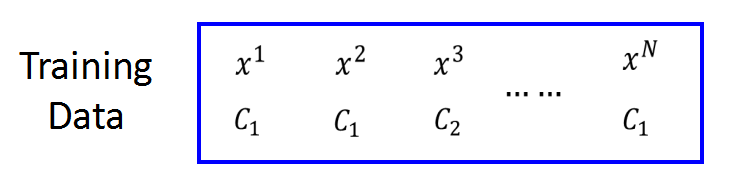
假设我们有N个训练数据,每个训练数据都标明了属于哪个类别(C1C_1C1或C2C_2C2)
并且假设这些数据是从fw,b(x)=Pw,b(C1∣x)f_{w,b}(x) = P_{w,b}(C_1|x)fw,b(x)=Pw,b(C1∣x)所产生的。
那么给定一组www和bbb,那如何计算某一组www和bbb产生这些数据的概率:
L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))⋯fw,b(xN) L(w,b) = f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))\cdots f_{w,b}(x^N) L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))⋯fw,b(xN)
其中x3x^3x3是属于C2C_2C2,因此它的计算方法有点不同。
最好的www和bbb会产生产生最大的L(w,b)L(w,b)L(w,b)
w∗,b∗=arg maxw,bL(w,b)
w^*,b^* = arg\,\max_{w,b}L(w,b)
w∗,b∗=argw,bmaxL(w,b)
做个数学上的转换,将上式右边取对数,并加上负号,变成计算最小的:
w∗,b∗=arg minw,b−lnL(w,b) w^*,b^* = arg\,\min_{w,b}-\ln L(w,b) w∗,b∗=argw,bmin−lnL(w,b)
取对数的好处是使得相乘变成相加:
−lnL(w,b)=−lnfw,b(x1)−lnfw,b(x2)−ln(1−fw,b(x3))⋯ -\ln L(w,b) = \\ -\ln f_{w,b}(x^1)\\ -\ln f_{w,b}(x^2)\\ -\ln (1-f_{w,b}(x^3)) \\ \cdots −lnL(w,b)=−lnfw,b(x1)−lnfw,b(x2)−ln(1−fw,b(x3))⋯
但是这个式子不好写个SUM的形式,因此需要做符号转换

如果y^n=1\hat{y}^n=1y^n=1则说明它属于类别C1C_1C1;若等于0,说明属于类别C2C_2C2,那么就有
−lnfw,b(x1)⟹−[y^1lnf(x1)+(1−y^1)ln(1−f(x1))]−lnfw,b(x2)⟹−[y^2lnf(x2)+(1−y^2)ln(1−f(x2))]−ln(1−fw,b(x3))⟹−[y^3lnf(x3)+(1−y^3)ln(1−f(x3))]⋯
-\ln f_{w,b}(x^1) \Longrightarrow -[\hat{y}^1 \ln f(x^1) + (1 - \hat{y}^1) \ln (1-f(x^1))]\\
-\ln f_{w,b}(x^2) \Longrightarrow -[\hat{y}^2 \ln f(x^2) + (1 - \hat{y}^2) \ln (1-f(x^2))]\\
-\ln (1-f_{w,b}(x^3)) \Longrightarrow -[\hat{y}^3 \ln f(x^3) + (1 - \hat{y}^3) \ln (1-f(x^3))]\\
\cdots
−lnfw,b(x1)⟹−[y^1lnf(x1)+(1−y^1)ln(1−f(x1))]−lnfw,b(x2)⟹−[y^2lnf(x2)+(1−y^2)ln(1−f(x2))]−ln(1−fw,b(x3))⟹−[y^3lnf(x3)+(1−y^3)ln(1−f(x3))]⋯
这样,就能得到一个函数:
因为y^n\hat{y}^ny^n取0或1,因此y^nlnf(xn)+(1−y^n)ln(1−f(xn))\hat{y}^n \ln f(x^n) + (1 - \hat{y}^n) \ln (1-f(x^n))y^nlnf(xn)+(1−y^n)ln(1−f(xn))中+号左右两边总有一个式子等于0。
L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))⋯fw,b(xN)−lnL(w,b)=−(lnfw,b(x1)+lnfw,b(x2)+ln(1−lnfw,b(x3))⋯=∑n−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))] \begin{aligned} L(w,b) &= f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))\cdots f_{w,b}(x^N) \\ -\ln L(w,b) &= -(\ln f_{w,b}(x^1) + \ln f_{w,b}(x^2) + ln(1-\ln f_{w,b}(x^3)) \cdots \\ &= \sum_n -[\hat{y}^n \ln f_{w,b}(x^n) + (1 - \hat{y}^n) \ln (1-f_{w,b}(x^n))] \\ \end{aligned} L(w,b)−lnL(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))⋯fw,b(xN)=−(lnfw,b(x1)+lnfw,b(x2)+ln(1−lnfw,b(x3))⋯=n∑−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))]
−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))]-[\hat{y}^n \ln f_{w,b}(x^n) + (1 - \hat{y}^n) \ln (1-f_{w,b}(x^n))]−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))]其实就是两个伯努利分布的交叉熵,交叉熵主要用于衡量两个分布有多接近,如果一模一样的话,那么就是0。

所以在逻辑回归中,定义一个函数的好坏就通过两个类别分布的交叉熵之和:

我们需要最小化这个交叉熵,也就是希望函数的输出和目标函数的输出越接近越好。
步骤3:找到最好的函数
−lnL(w,b)=∑n−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))]
-\ln L(w,b) = \sum_n -[\hat{y}^n \ln f_{w,b}(x^n) + (1 - \hat{y}^n) \ln (1-f_{w,b}(x^n))] \\
−lnL(w,b)=n∑−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))]
找到最好的函数需要找到一组www和bbb使得上式的结果最小。
计算该式对w中某个特征的微分。
−lnL(w,b)∂wi=∑n−[y^n∂lnfw,b(xn)∂wi+(1−y^n)∂ln(1−fw,b(xn))∂wi] \frac{-\ln L(w,b)}{\partial w_i} = \sum_n -[\hat{y}^n \frac{\partial \ln f_{w,b}(x^n)}{\partial w_i} + (1 - \hat{y}^n) \frac{ \partial \ln (1-f_{w,b}(x^n))}{\partial w_i}] ∂wi−lnL(w,b)=n∑−[y^n∂wi∂lnfw,b(xn)+(1−y^n)∂wi∂ln(1−fw,b(xn))]
其中fw,b(x)=σ(z)=11+exp(−z)f_{w,b}(x) = \sigma(z) =\frac{1}{1 + exp(-z)}fw,b(x)=σ(z)=1+exp(−z)1 ,z=w⋅x+b=∑iwixi+bz = w \cdot x + b = \sum_i w_ix_i + bz=w⋅x+b=∑iwixi+b
一项一项来求,左项可以写成
∂lnfw,b(x)∂wi=∂lnfw,b(x)∂z∂z∂wi \frac{\partial \ln f_{w,b}(x)}{\partial w_i} = \frac{\partial \ln f_{w,b}(x)}{\partial z} \frac{\partial z}{\partial w_i} ∂wi∂lnfw,b(x)=∂z∂lnfw,b(x)∂wi∂z
由zzz的表达式知 ∂z∂wi=xi\frac{\partial z}{\partial w_i} = x_i∂wi∂z=xi
∂lnfw,b(x)∂z=∂lnσ(z)∂z=1σ(z)∂σ(z)∂z=1σ(z)σ(z)(1−σ(z))=(1−σ(z)) \frac{\partial \ln f_{w,b}(x)}{\partial z} = \frac{\partial \ln \sigma(z)}{\partial z} = \frac{1}{\sigma(z)} \frac{\partial \sigma(z)}{\partial z} = \frac{1}{\sigma(z)} \sigma(z)(1-\sigma(z)) = (1 - \sigma(z)) ∂z∂lnfw,b(x)=∂z∂lnσ(z)=σ(z)1∂z∂σ(z)=σ(z)1σ(z)(1−σ(z))=(1−σ(z))
其中∂σ(z)∂z=σ(z)(1−σ(z))\frac{\partial \sigma(z)}{\partial z} = \sigma(z)(1-\sigma(z))∂z∂σ(z)=σ(z)(1−σ(z)) 证明如下:
σ′(z)=(11+e−z)′=0−(−e−z)(1+e−z)2=1+e−z−1(1+e−z)2=1(1+e−z)(1−1(1+e−z))=σ(z)(1−σ(z)) \begin{aligned} \sigma'(z) &= (\frac{1}{1+e^{-z}})' \\ &= \frac{0 - (-e^{-z})}{(1+e^{-z})^{2}} \\ &= \frac{1+e^{-z}-1}{(1+e^{-z})^{2}} \\ &= \frac{1}{(1+e^{-z})}(1-\frac{1}{(1+e^{-z})}) \\ &= \sigma(z)(1-\sigma(z))\\ \end{aligned} σ′(z)=(1+e−z1)′=(1+e−z)20−(−e−z)=(1+e−z)21+e−z−1=(1+e−z)1(1−(1+e−z)1)=σ(z)(1−σ(z))
而右项
∂ln(1−fw,b(x))∂wi=∂ln(1−fw,b(x))∂σ(z)∂z∂wi∂z∂wi=xi \frac{ \partial \ln (1-f_{w,b}(x))}{\partial w_i} = \frac{ \partial \ln (1-f_{w,b}(x))}{\partial \sigma(z)} \frac{\partial z}{\partial w_i} \quad \frac{\partial z}{\partial w_i} = x_i ∂wi∂ln(1−fw,b(x))=∂σ(z)∂ln(1−fw,b(x))∂wi∂z∂wi∂z=xi
也就是
∂ln(1−σ(z))∂σ(z)=−11−σ(z)∂zσ(z)=−11−σ(z)σ(z)(1−σ(z))=−σ(z) \frac{ \partial \ln (1-\sigma(z))}{\partial \sigma(z)} = - \frac{1}{1- \sigma(z)} \frac{\partial z}{\sigma(z)} = - \frac{1}{1- \sigma(z)} \sigma(z) (1-\sigma(z)) = -\sigma(z) ∂σ(z)∂ln(1−σ(z))=−1−σ(z)1σ(z)∂z=−1−σ(z)1σ(z)(1−σ(z))=−σ(z)
所以
−lnL(w,b)∂wi=∑n−[y^n∂lnfw,b(xn)∂wi+(1−y^n)∂ln(1−fw,b(xn))∂wi]=∑n−[y^n(1−fw,b(xn))xin−(1−y^n)fw,b(xn)xin]=∑n−[y^n−y^nfw,b(xn)−fw,b(xn)+y^nfw,b(xn)]xin=∑n−(y^n−fw,b(xn))xin \begin{aligned} \frac{-\ln L(w,b)}{\partial w_i} &= \sum_n - [\hat{y}^n \frac{\partial \ln f_{w,b}(x^n)}{\partial w_i} + (1 - \hat{y}^n) \frac{ \partial \ln (1-f_{w,b}(x^n))}{\partial w_i}] \\ &= \sum_n -[\hat{y}^n(1-f_{w,b}(x^n))x_i^n - (1 - \hat{y}^n)f_{w,b}(x^n)x_i^n] \\ &= \sum_n -[\hat{y}^n - \bcancel{\hat{y}^n f_{w,b}(x^n)} - f_{w,b}(x^n) + \bcancel{\hat{y}^nf_{w,b}(x^n)}]x_i^n \\ &= \sum_n -(\hat{y}^n - f_{w,b}(x^n))x_i^n \end{aligned} ∂wi−lnL(w,b)=n∑−[y^n∂wi∂lnfw,b(xn)+(1−y^n)∂wi∂ln(1−fw,b(xn))]=n∑−[y^n(1−fw,b(xn))xin−(1−y^n)fw,b(xn)xin]=n∑−[y^n−y^nfw,b(xn)−fw,b(xn)+y^nfw,b(xn)]xin=n∑−(y^n−fw,b(xn))xin
得到的式子很简单。如果用梯度下降算法来更新它的话,可以写成:
wi←wi−η∑n−(y^n−fw,b(xn))xin w_i \leftarrow w_i - \eta \sum_n -(\hat{y}^n - f_{w,b}(x^n))x_i^n wi←wi−ηn∑−(y^n−fw,b(xn))xin
y^n−fw,b(xn)\hat{y}^n - f_{w,b}(x^n)y^n−fw,b(xn)表示理想的目标与模型的输出的差距,如果差距越大,
那么更新的量应该要越大。
接下来比较下逻辑回归和线性回归更新时的式子:
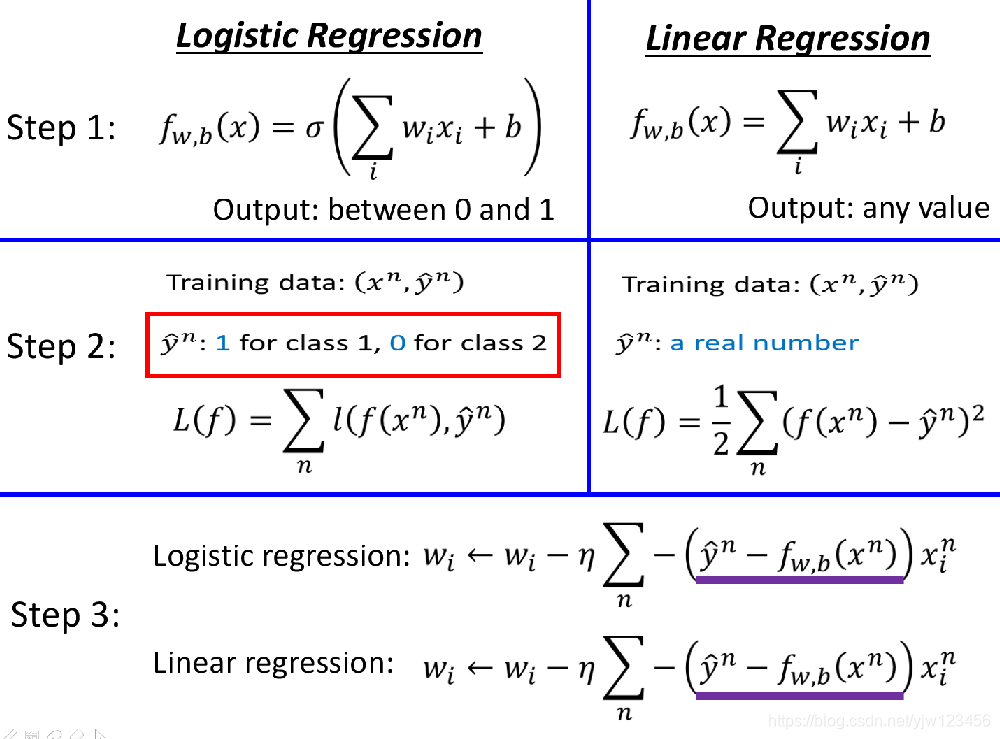
会发现表达式是一模一样的。唯一不同的是逻辑回归的y^n\hat{y}^ny^n取0或1,f是0~1之间的数值;而线性回归的y^n\hat{y}^ny^n是任意实数,输出也可以是任何实数。
生成模型VS判别模型
我们上面讨论的逻辑回归是判别模型(Discriminative),用高斯分布描述的概率分布模型是生成模型(Generative)。
它们的函数集是一样的 P(C1∣x)=σ(w⋅x+b)P(C_1|x) = \sigma(w \cdot x + b)P(C1∣x)=σ(w⋅x+b)
用逻辑回归能直接找出www和bbb;如果是生成模型,那么需要找到μ1,μ2,Σ−1\mu^1,\mu^2,\Sigma^{-1}μ1,μ2,Σ−1,进而求出wTw^TwT和bbb
根据同一组训练数据,同样的函数集,上面两种模型会得到不同的函数。
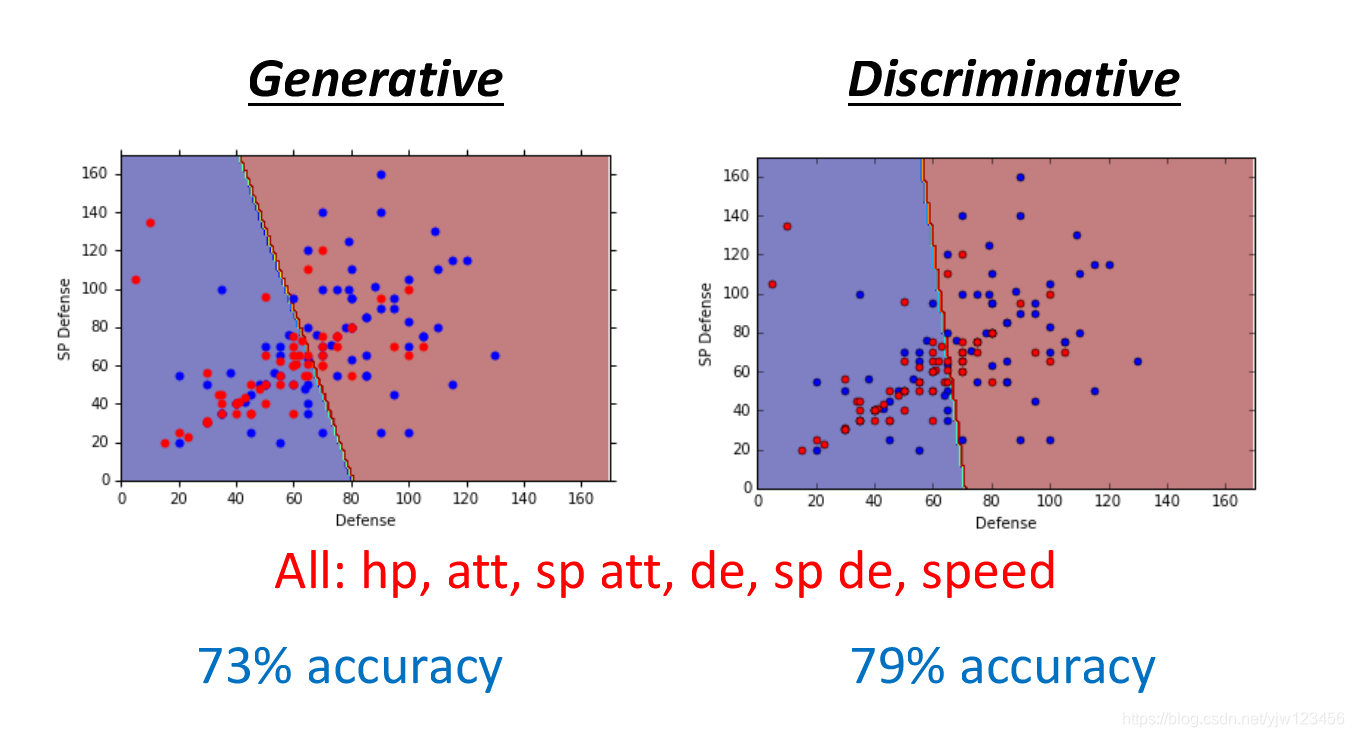
如果用上所有的特征,判别模型的准确率更好。
假设有一个非常简单的二元分类问题,每个数据都有两个特征。
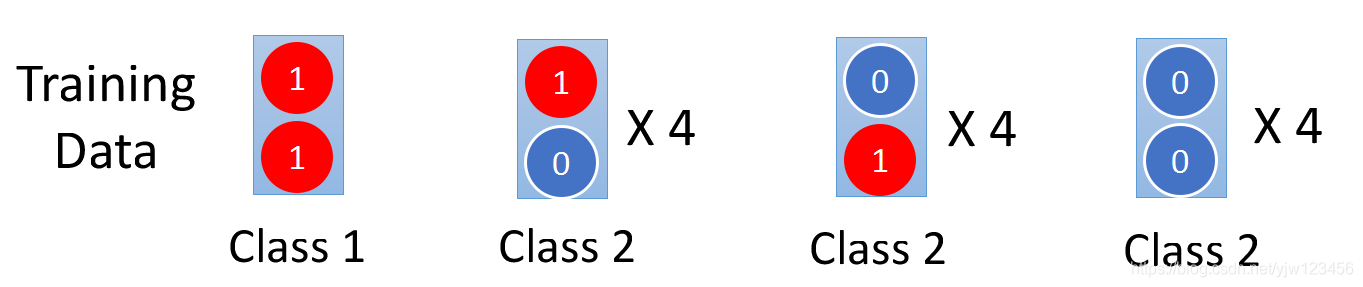
Class1我们只有一份数据,它的两个特征都是1;Class2有12份数据,如上。
如果给一份测试数据,它的两个特征都是1:
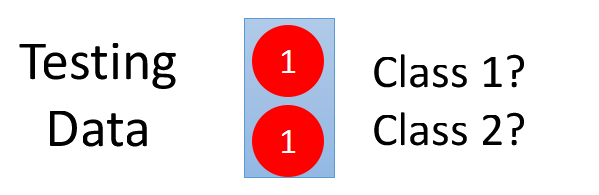
那么它属于哪个类别的概率大呢?
我们先来看下生成模型,选用朴素贝叶斯模型,朴素说的是每个特征都是独立的。
P(x∣Ci)=P(x1∣Ci)P(x2∣Ci)P(x|C_i) = P(x_1|C_i)P(x_2|C_i)P(x∣Ci)=P(x1∣Ci)P(x2∣Ci)
P(C1)=113P(C_1) = \frac{1}{13}P(C1)=131 给定类别C1C_1C1,第一个特征是1的几率P(x1=1∣C1)=1P(x_1 = 1|C_1) = 1P(x1=1∣C1)=1,第二个特征是1的几率P(x2=1∣C1)=1P(x_2 = 1|C_1) = 1P(x2=1∣C1)=1,也是1。
P(C2)=1213P(C_2) = \frac{12}{13}P(C2)=1312 ,给定类别C2C_2C2,第一个特征是1的几率P(x1=1∣C1)=13P(x_1 = 1|C_1) = \frac{1}{3}P(x1=1∣C1)=31,第二个特征是1的几率P(x2=1∣C1)=13P(x_2 = 1|C_1) = \frac{1}{3}P(x2=1∣C1)=31
接下来计算这个测试数据属于类别1的几率
P(C1∣x)=p(x∣C1)P(C1)p(x∣C1)P(C1)+p(x∣C2)P(C2) P(C_1|x) = \frac{p(x|C_1)P(C_1)}{p(x|C_1)P(C_1) + p(x|C_2)P(C_2)} \\ P(C1∣x)=p(x∣C1)P(C1)+p(x∣C2)P(C2)p(x∣C1)P(C1)
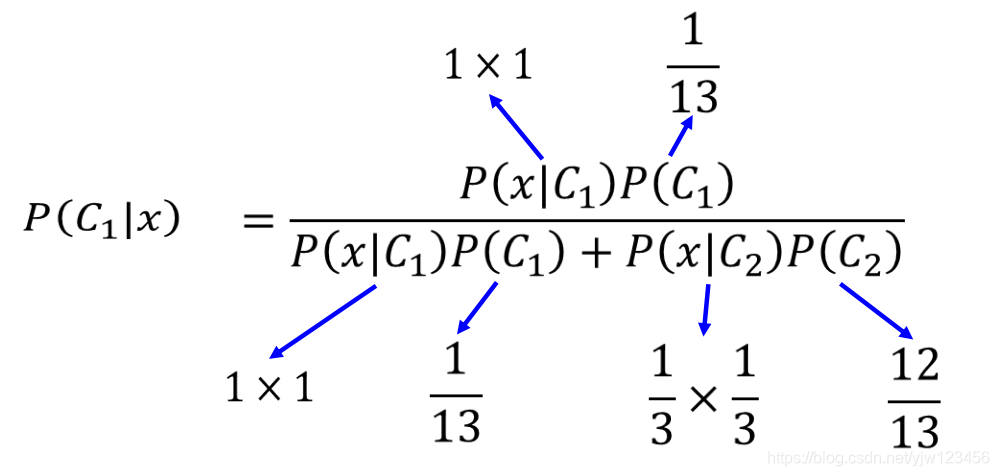
计算得P(C1∣x)<0.5P(C_1|x) < 0.5P(C1∣x)<0.5 ,因此判断它属于类别2;而用逻辑回归判断它属于类别1。
多分类问题
多分类问题是指类别超过2个的分类问题。
假设有3个类别,每个类别都有两组参数,我们怎么计算某个样本属于这三个类别的几率分别是多少。
我们计算z1,z2,z3z_1,z_2,z_3z1,z2,z3
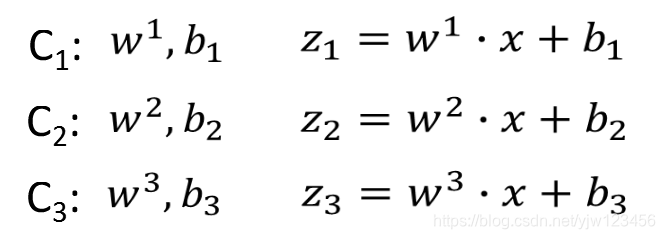
假设有个函数
Softmax,它的输入就是z1,z2,z3z_1,z_2,z_3z1,z2,z3,输出y1,y2,y3y_1,y_2,y_3y1,y2,y3
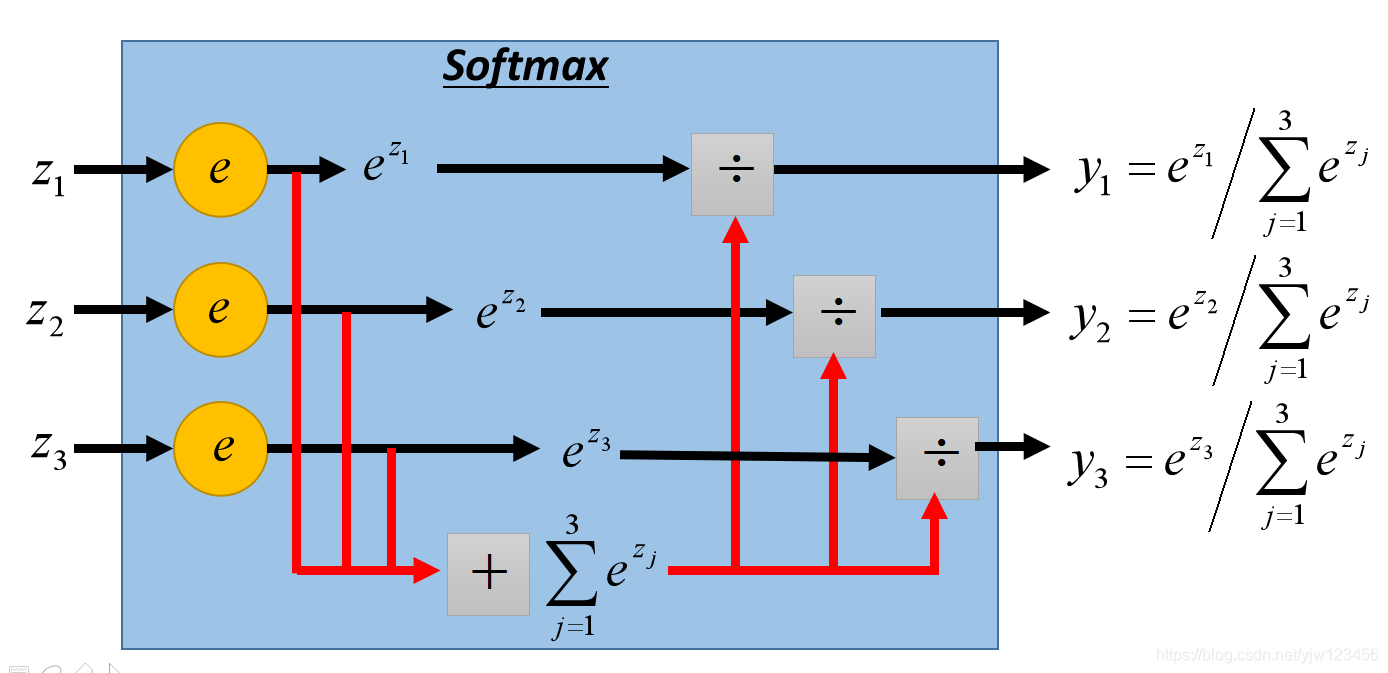
假设输入是3,1,-3
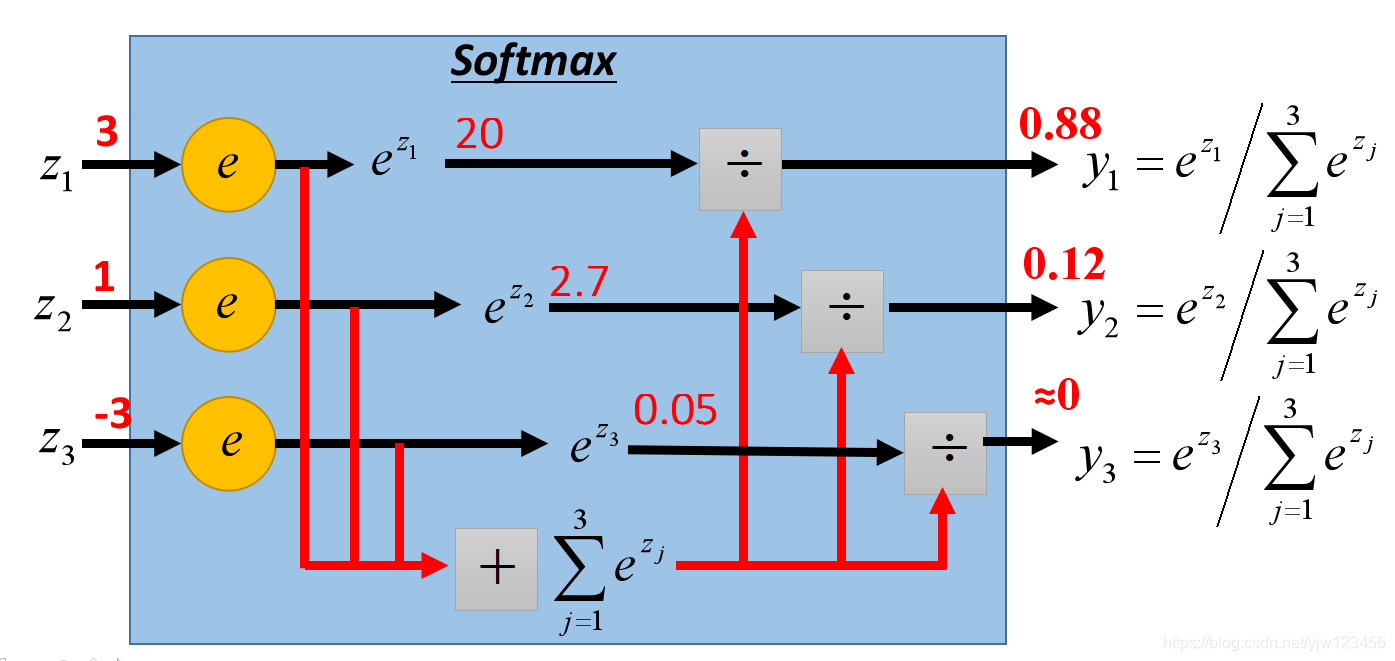
首先取
e的指数,得到20,2.7,0.05 再把这些数加起来得到22.75,输出就是根据
e的指数除以这个加起来的总数。
可以把这些输出当成概率,它们的和刚好是1。yi=P(Ci∣x)y_i = P(C_i|x)yi=P(Ci∣x)
我们把z1,z2,z3z_1,z_2,z_3z1,z2,z3经过
Softmax函数后,得到y1,y2,y3y_1,y_2,y_3y1,y2,y3,我们要计算这些输出和对应的target(实际类别)的交叉熵。
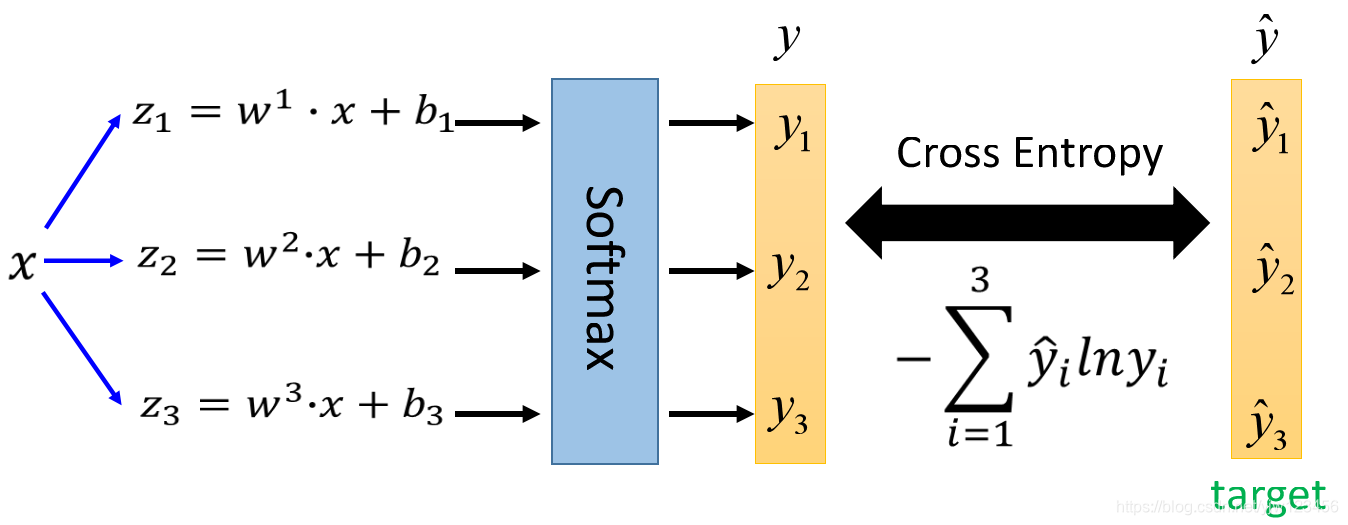
y^\hat{y}y^的表示如下:
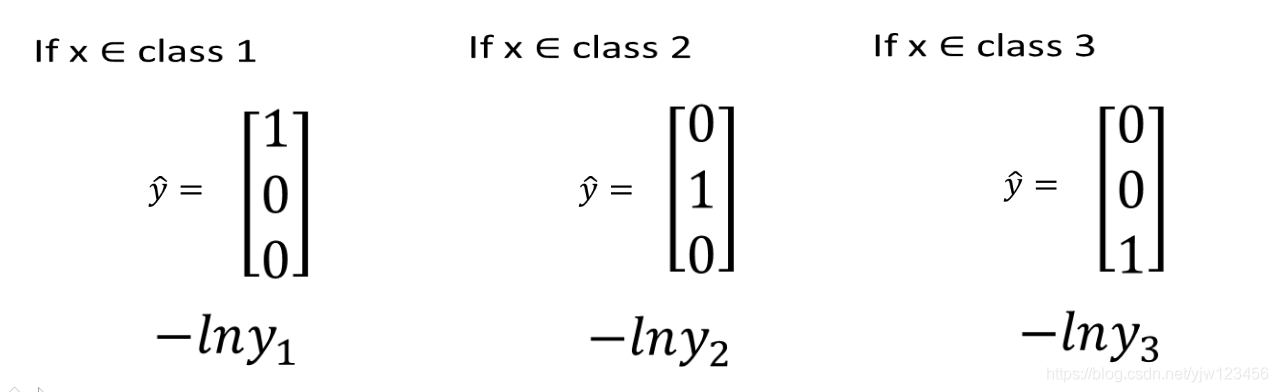
逻辑回归的限制
逻辑回归其实有很大的限制的,以一个简单的二分类问题来举例。
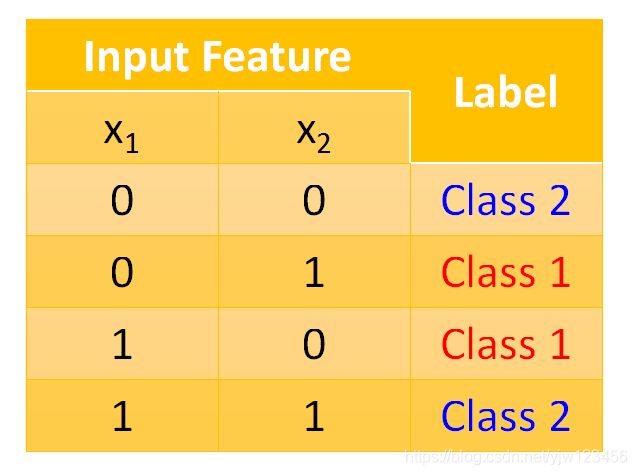
它只有两个特征,如果都是0,则属于类别2;如果x1=0,x2=1x_1=0,x_2=1x1=0,x2=1则属于类别1。
把这四个样本画到二维坐标上是下面这个样子,蓝色的点是类别2;红色的点是类别1。
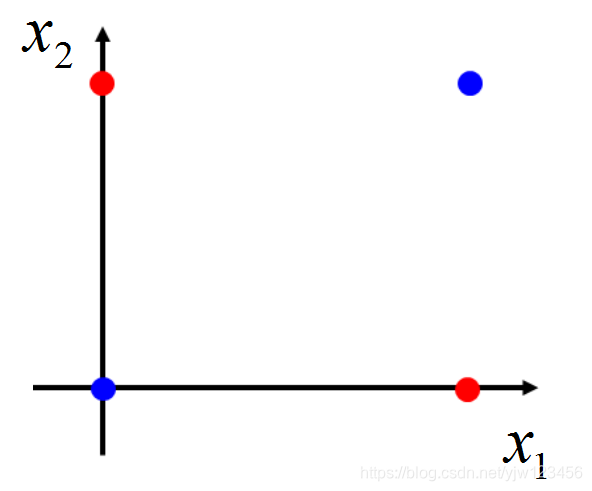
假设现在用逻辑回归模型来训练z=w1x1+w2x2+bz = w_1x_1 + w_2x_2 + bz=w1x1+w2x2+b
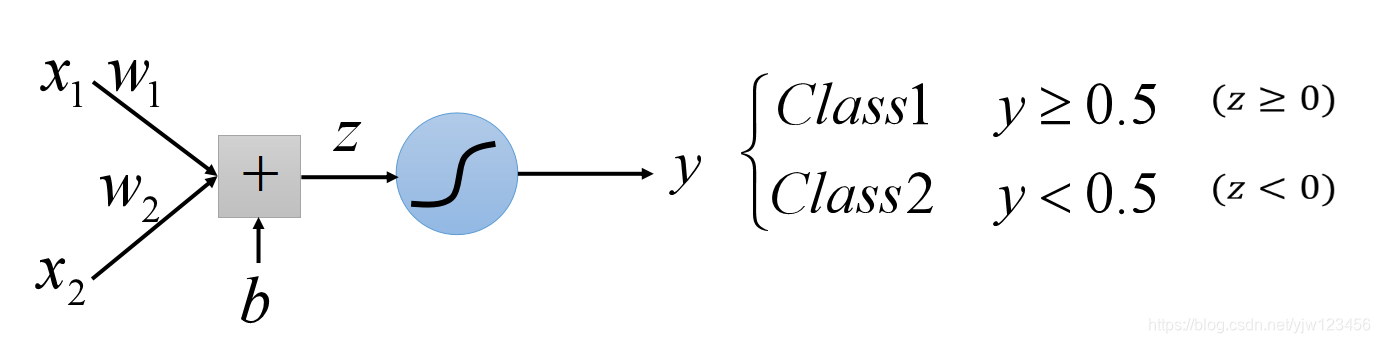
输入x1,x2x_1,x_2x1,x2,分别把它们乘以w1,w2w_1,w_2w1,w2加上bbb得到zzz,代入
Sigmoid函数得到输出yyy。
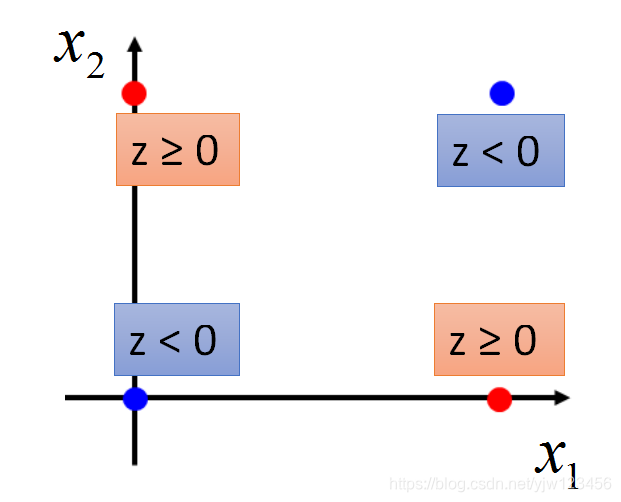
对红色的点来说,zzz要大于等于0,对蓝色的点来说zzz要<0。我们做的到吗?做不到。
zzz是一条直线,因为逻辑回归能做到的事情是画一条这样的直线其中一边属于类别1,另一边属于类别2。
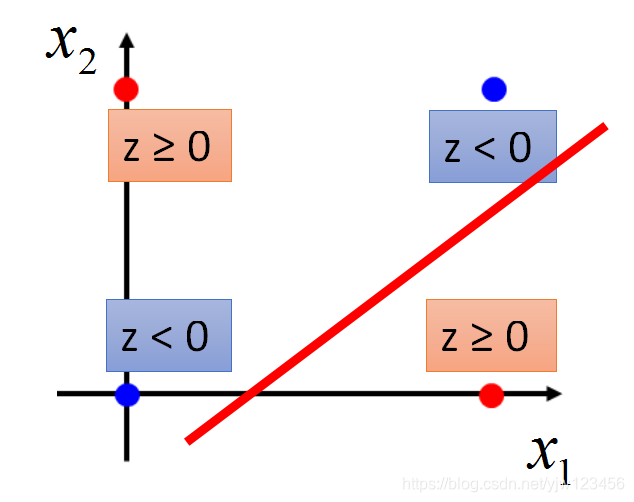
不管怎么画,都无法画出满足条件的直线。
那么怎么办呢,还是有办法的,可以做特征转换。把蓝色点和红点转换成一条直线的两边。
比如可以这样,重新定义特征,把原特征x1x_1x1和[0,0]T[0,0]^T[0,0]T的距离定义成新特征x1′x^{\prime}_1x1′,把原特征x2x_2x2和[1,1]T[1,1]^T[1,1]T的距离定义成新特征x2′x^{\prime}_2x2′
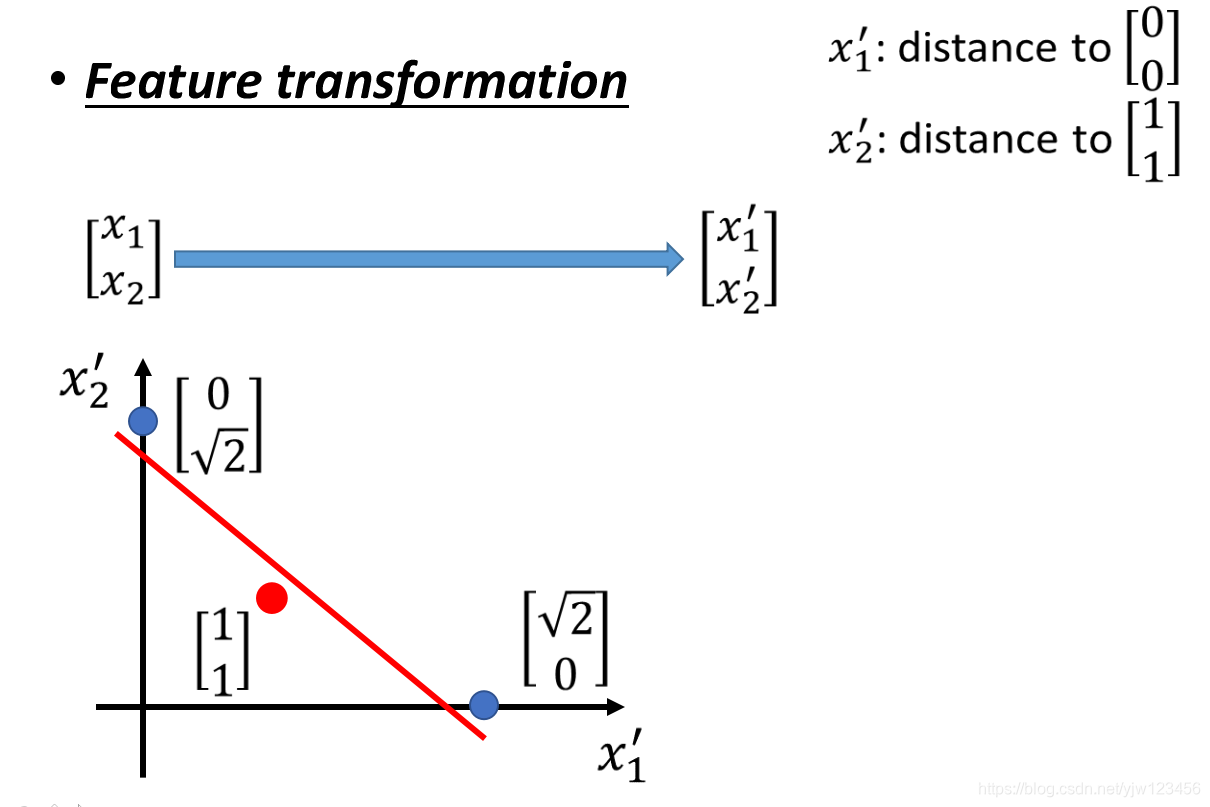
比如原特征[0,0]T[0,0]^T[0,0]T和[0,0]T[0,0]^T[0,0]T的距离是0,和[1,1]T[1,1]^T[1,1]T的距离是2\sqrt{2}2,就转换成上图左上角蓝色的点。
然后就可以画一条线将红蓝点分开。
但是特征转换并不总是那么的有用,因为这需要领域知识,要知道该怎么转换。
其实特征转换可以看很多个逻辑回归模型叠加的结果。
可以把x1x_1x1转换成x1′x^{\prime}_1x1′以及x2x_2x2转换成x2′x^{\prime}_2x2′看成是两个逻辑回归模型的结果。
也就是说,如下图蓝色的逻辑回归,输入是x1,x2x_1,x_2x1,x2输出就是x1′x^{\prime}_1x1′;而绿色的逻辑回归,输入是x1,x2x_1,x_2x1,x2输出就是x2′x^{\prime}_2x2′。它们两个做特征转换,而红色的作用就是分类。
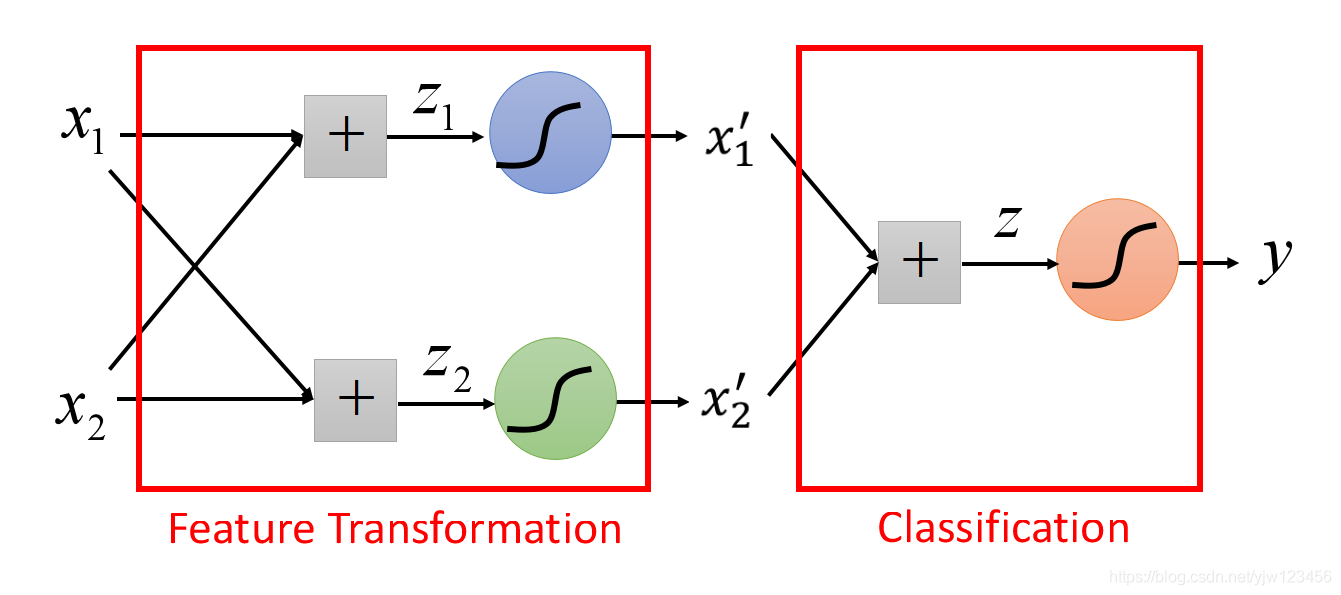
我们继续用刚才讲的例子来说明。
假设蓝色的逻辑回归的参数是-1(bbb),-2(w1w_1w1),2(w2w_2w2),就可以计算出x1′x^{\prime}_1x1′的值。
z=w1x1+w2x2+bz = w_1x_1 + w_2x_2 + bz=w1x1+w2x2+b
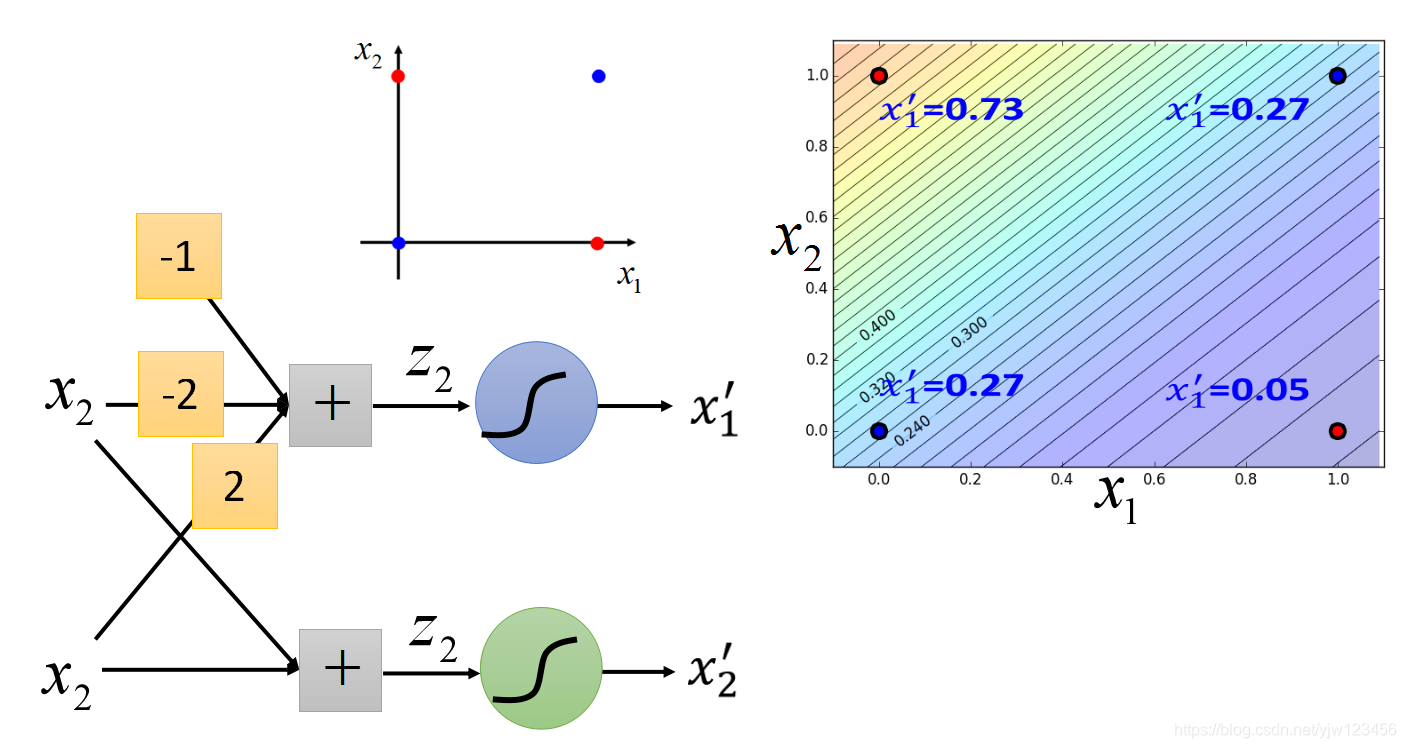
也就可以计算出四个点的x1′x^{\prime}_1x1′,同理可以计算出四个点的x2′x^{\prime}_2x2′。
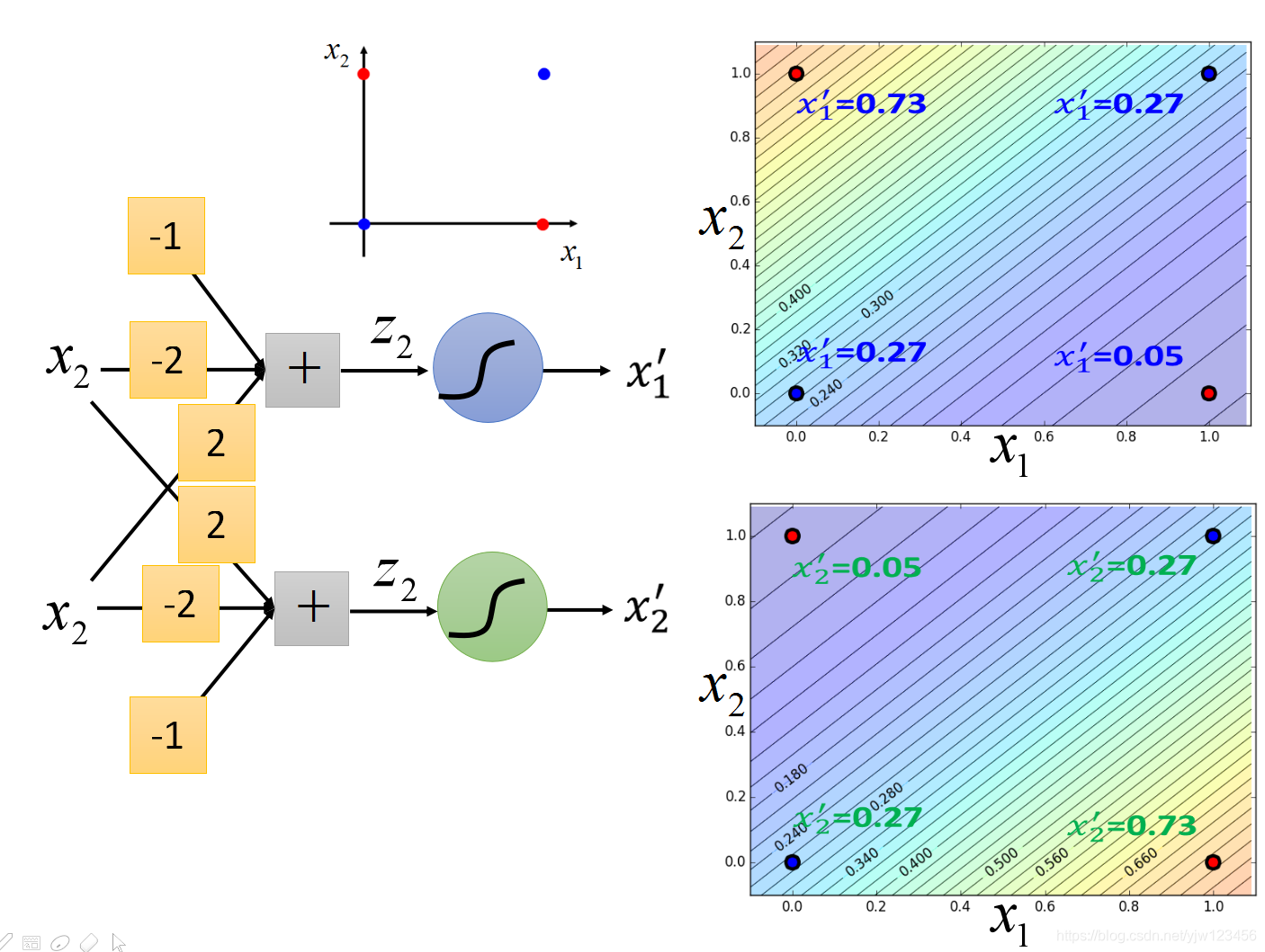
接下来就可以根据这些x1′,x2′x^{\prime}_1,x^{\prime}_2x1′,x2′重新画出一个新的图形。
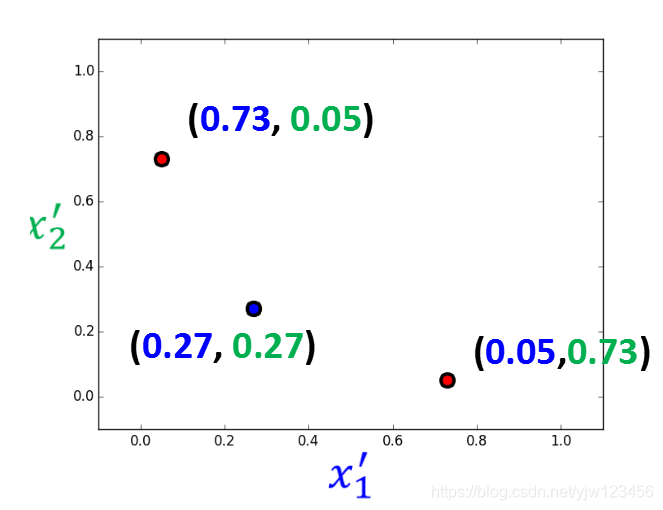
而红色的逻辑回归测试的就是x1′,x2′x^{\prime}_1,x^{\prime}_2x1′,x2′,也就可以画出一条直线将它们分开。
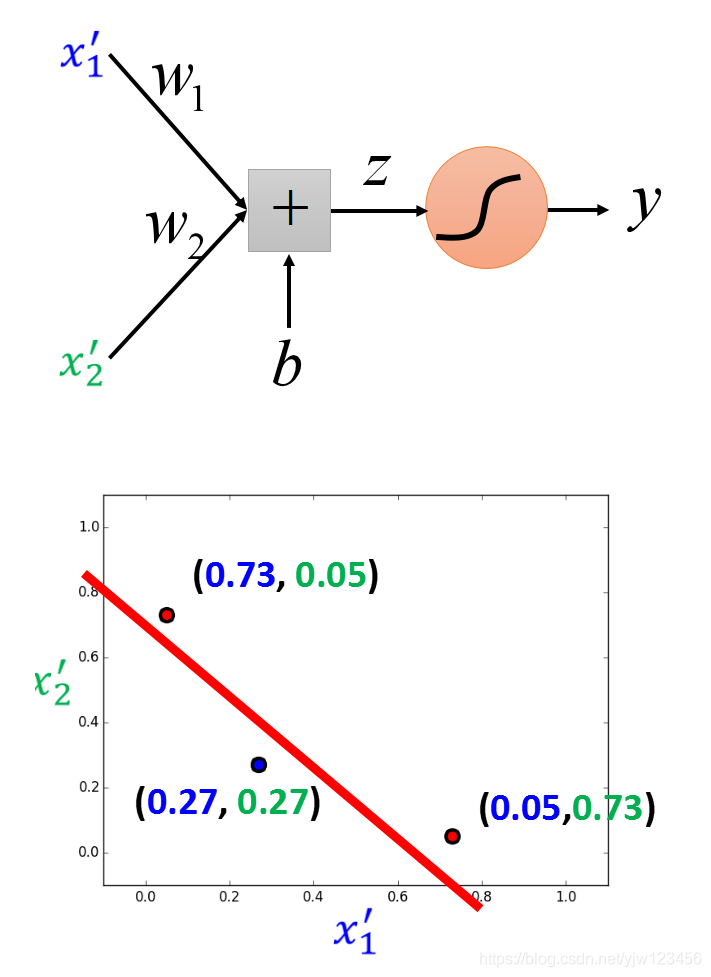
我们可以把逻辑回归串接起来,一部分做特征转换,最后用一个做真正的分类。
那么问题来了,如何找到这些逻辑回归模型的参数呢?
这些逻辑回归的参数可以一起学习到的,只要告诉输入和输出,就可以一次把所有的逻辑回归的参数学习出来。
我们把上面每个逻辑回归模型叫做神经元,每个神经元串接起来后叫做神经网络,这就是深度学习
- 点赞
- 收藏
- 分享
- 文章举报
 愤怒的可乐
博客专家
发布了151 篇原创文章 · 获赞 186 · 访问量 14万+
私信
关注
愤怒的可乐
博客专家
发布了151 篇原创文章 · 获赞 186 · 访问量 14万+
私信
关注
- 李宏毅机器学习——学习笔记(3)
- 李宏毅机器学习笔记——回归
- 机器学习_线性回归和逻辑回归(及python)
- 14、【李宏毅机器学习(2017)】Unsupervised Learning: Word Embedding(无监督学习:词嵌入)
- 机器学习——逻辑回归
- [机器学习入门] 李宏毅机器学习课程回顾 + 接下来的学习声明
- 机器学习笔记 (2)-逻辑回归模型
- 机器学习——逻辑回归
- Python数据分析与机器学习-Python实现逻辑回归与梯度下降策略
- 李宏毅机器学习 P12 HW2 Winner or Loser 笔记(不使用框架实现使用MBGD优化方法和z_score标准化的logistic regression模型)
- 李宏毅机器学习-task1
- 【机器学习】逻辑回归
- 李宏毅机器学习-3
- 李宏毅机器学习笔记
- 机器学习----逻辑回归
- 机器学习入门笔记- 李宏毅-L1L2
- 机器学习李宏毅第五讲 误差来源讨论
- 【机器学习(李宏毅)】 二、Regression: Case Study
- 机器学习 Python实现逻辑回归
- 李宏毅笔记机器学习(四)——Regression——Demo
