李宏毅机器学习——梯度下降
梯度下降回顾
在前篇文章中介绍的机器学习三步走第三步中,我们需要解决下面优化问题:
θ∗=arg minθL(θ)\theta^*=arg\,\min_{\theta}L(\theta)θ∗=argminθL(θ)
假设θ\thetaθ向量有两个属性{θ1,θ2}\{\theta_1,\theta_2\}{θ1,θ2}
初始从θ0\theta^0θ0开始,
θ0=[θ10θ20] \theta^0 =\left[ \begin{matrix} \theta^0_1 \\ \theta^0_2 \end{matrix} \right] θ0=[θ10θ20]
接下来计算
[θ11θ21]=[θ10θ20]−η[∂L(θ10)/∂θ1∂L(θ20)/∂θ2] \left[ \begin{matrix} \theta^1_1 \\ \theta^1_2 \end{matrix} \right] = \left[ \begin{matrix} \theta^0_1 \\ \theta^0_2 \end{matrix} \right] -\eta \left[ \begin{matrix} \partial L(\theta_1^0) / \partial \theta_1 \\ \partial L(\theta_2^0) / \partial \theta_2\end{matrix} \right] [θ11θ21]=[θ10θ20]−η[∂L(θ10)/∂θ1∂L(θ20)/∂θ2]
这个步骤可以反复进行,再计算一次的话:
[θ12θ22]=[θ11θ21]−η[∂L(θ11)/∂θ1∂L(θ21)/∂θ2]
\left[ \begin{matrix}
\theta^2_1 \\
\theta^2_2
\end{matrix} \right]
= \left[ \begin{matrix}
\theta^1_1 \\
\theta^1_2
\end{matrix} \right] -\eta
\left[ \begin{matrix} \partial L(\theta_1^1) / \partial \theta_1 \\
\partial L(\theta_2^1) / \partial \theta_2\end{matrix} \right]
[θ12θ22]=[θ11θ21]−η[∂L(θ11)/∂θ1∂L(θ21)/∂θ2]
其中η\etaη是初始学习率(learning rate)
上面的式子可以写得更加简洁:
∇L(θ)=[∂L(θ1)/∂θ1∂L(θ2)/∂θ2]
\nabla L(\theta) = \left[ \begin{matrix} \partial L(\theta_1) / \partial \theta_1 \\ \partial L(\theta_2) / \partial \theta_2\end{matrix} \right]
∇L(θ)=[∂L(θ1)/∂θ1∂L(θ2)/∂θ2]
∇L(θ)\nabla L(\theta)∇L(θ)叫做梯度。
也就是说:
[θ11θ21]=[θ10θ20]−η[∂L(θ10)/∂θ1∂L(θ20)/∂θ2]⟹θ1=θ0−η∇L(θ0) \left[ \begin{matrix} \theta^1_1 \\ \theta^1_2 \end{matrix} \right] = \left[ \begin{matrix} \theta^0_1 \\ \theta^0_2 \end{matrix} \right] -\eta \left[ \begin{matrix} \partial L(\theta_1^0) / \partial \theta_1 \\ \partial L(\theta_2^0) / \partial \theta_2\end{matrix} \right] \Longrightarrow \theta^1 = \theta^0 - \eta \nabla L(\theta^0) [θ11θ21]=[θ10θ20]−η[∂L(θ10)/∂θ1∂L(θ20)/∂θ2]⟹θ1=θ0−η∇L(θ0)

红色箭头是梯度向量,蓝色箭头是移动的方向。
小心的调整学习率

每种颜色都是不同的学习率。
如果学习率刚刚好,就像红色箭头所示;如果过小则向蓝色箭头,显得步长太小了;
若太大则像绿色箭头,那么永远到不了低点;甚至还可以过大,导致像黄色箭头那样。
如果是参数是一维或二维我们还可以画出这种图,如果参数超过3就没办法了。
我们还可以通过参数的变化来观察损失的变化。
可以通过观察损失函数的下降速度

x轴是学习率,y轴是Loss函数的值
因此学习率的调整很重要,简单的原则是:
- 开始时由于远离目标,因此使用大一点的学习率
- 在几次更新后,靠近目标了,因此减小学习率
- 每个参数给不同的学习率
比如可以选择ηt=η/t+1\eta^t = \eta / \sqrt{t +1}ηt=η/t+1,其中ttt是计算的次数,但是这样还不够。
接下来介绍一种比较好的梯度下降算法:Adagrad。
Adagrad
每个参数的学习率都除上之前算出来的微分值的均方根。
一般的梯度下降(批梯度下降,Vanilla Gradient descent)是这样的:
wt+1←wt−ηtgtw^{t+1} \leftarrow w^t - \eta^t g^twt+1←wt−ηtgt 其中www是某一个参数,因为在做adagrad时,每个参数都有不同的学习率。
所以我们分别考虑每个参数。
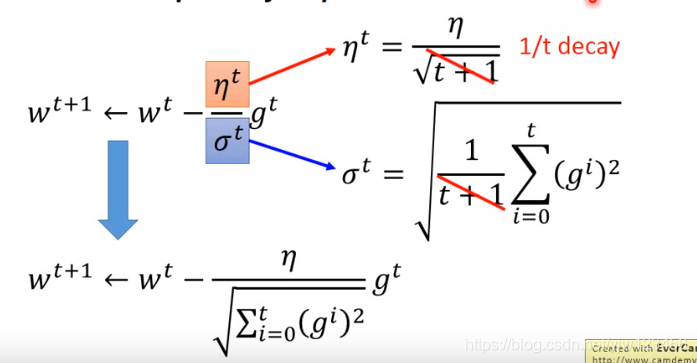
ηt=ηt+1,gt=∂L(θt)∂w
\eta^t = \frac{\eta} {\sqrt{t +1}},g^t = \frac{\partial L(\theta ^t)}{\partial w}
ηt=t+1η,gt=∂w∂L(θt)
而Adagrad的做法是:
wt+1←wt−ηtσtgt w^{t+1} \leftarrow w^t - \frac{\eta^t}{\sigma^t}g^t wt+1←wt−σtηtgt
σt\sigma^tσt是过去所有微分值的均方根。这个值对每个参数而言都是不一样的,因此是参数独立的。
我们来举个例子,假设初值为w0w^0w0。

整个Adagrad的式子式是可以简化的:
再回头来看下批梯度下降算法:
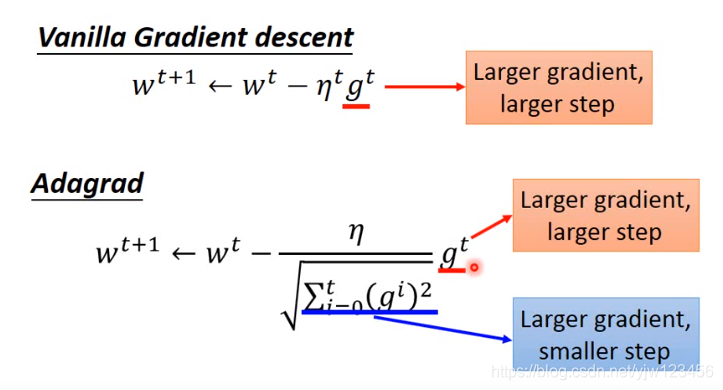
批梯度下降算法是梯度越大,步伐就越大;
而Adagrad是分子上,梯度越大,步伐越大;分母上,梯度越大,步伐越小。这里是否感觉有些矛盾。
我们来考虑一个二次函数: y=ax2+bx+cy = ax^2 + bx + cy=ax2+bx+c,它的图像如下:

把上式对xxx做微分并取绝对值,得
∣∂y∂x∣=∣2ax+b∣
|\frac{\partial y}{\partial x}| = |2ax + b|
∣∂x∂y∣=∣2ax+b∣
它的图形为:

在二次函数上,假设初始点为x0x_0x0,最低点是−b2a-\frac{b}{2a}−2ab此时如果想找到最好的步伐多少

其实x0x_0x0和−b2a-\frac{b}{2a}−2ab之间的距离 ∣x0+b2a∣|x_0 + \frac{b}{2a}|∣x0+2ab∣,整理一下可得∣2ax0+b∣2a\frac{|2ax_0 + b|}{2a}2a∣2ax0+b∣
而∣2ax0+b∣|2ax_0 + b|∣2ax0+b∣就是x0x_0x0点的一次微分。

如果某点的微分值越大,则距离最低点越远;如果踏出去的步伐和微分大小成正比,则有可能是最好的步伐。
上面我们只考虑了一个参数,如果考虑多个参数上面的结论则不一定成立。
假设有两个参数,如果只考虑参数1,它的图像为:

其中a点的微分值大于b点,a点距离最低点更远。如果也考虑参数w2w_2w2,它的图像是绿色的那个:
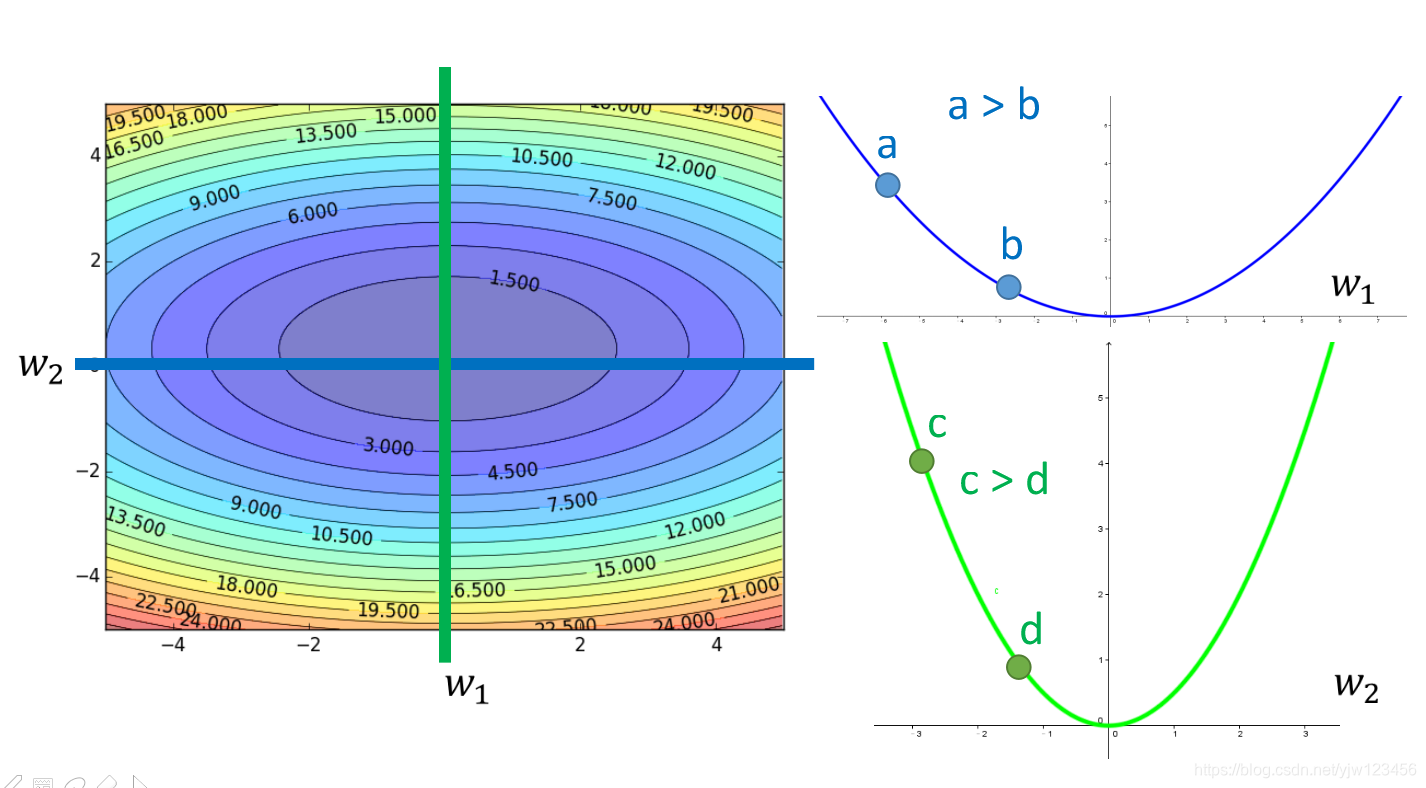
那,如果同时考虑这两个参数,如果同时考虑a点对w1w_1w1的微分,c点对w2w_2w2的微分。
c点处的微分值比较大,a点处的微分值小于它,但是c离低点比a离低点更近。
我们再回头看下最好的微分∣2ax0+b∣2a\frac{|2ax_0 + b|}{2a}2a∣2ax0+b∣,发现它的分母上有个2a2a2a。
我们把函数做二次微分得:∂2y∂x2=2a\frac{\partial^2y}{\partial x^2} = 2a∂x2∂2y=2a
也就是说,最好的步伐,它不仅和一次微分成正比,还和二次微分成反比。
那它和Adagrad的关系是什么?
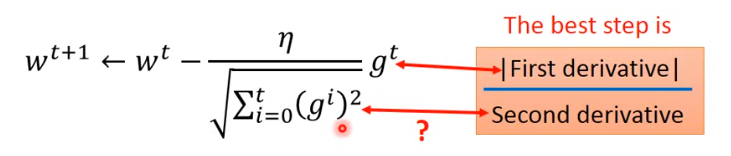
我们再来看下adagrad:gtg^tgt就是一次微分,那么它的分母是怎么和二次微分关联的呢?(derivative,导数)
adagrad用一次微分来估计二次微分:

我们考虑二次微分较小的图形(图左)和二次微分较大的图形(图右)。
然后把它们一次微分(一次微分)2\sqrt{(一次微分)^2}(一次微分)2的图形考虑进来:

我们在一次微分图形上取很多个点,可以发现在二次微分较小的图形中,它的一次微分通常也较小。
而Adagrad中的∑i=0t(gi)2\sqrt{\sum_{i=0}^t(g^i)^2}∑i=0t(gi)2就反映了二次微分的大小。
通过Adagrad实现梯度下降的代码:
def gradient_descent(): x_data = [338, 333, 328, 207, 226, 25, 179, 60, 208, 606] y_data = [640, 633, 619, 393, 428, 27, 193, 66, 226, 1591] b = -120 w = -4 lr = 1 # 学习率 lr_b = 0 # b的学习率 lr_w = 0 # w的学习率 iteration = 10000 #迭代次数 for i in range(iteration): b_grad = 0.0 w_grad = 0.0 for n in range(len(x_data)): w_grad = w_grad - 2.0 * (y_data[n] - (b + w * x_data[n])) * x_data[n] b_grad = b_grad - 2.0 * (y_data[n] - (b + w * x_data[n])) * 1.0 lr_b = lr_b + b_grad ** 2 lr_w = lr_w + w_grad ** 2 b = b - lr/np.sqrt(lr_b) * b_grad w = w - lr/np.sqrt(lr_w) * w_grad print(b,w)
随机梯度下降法
随机梯度下降法( Stochastic Gradient Descent)可以训练的更快。
上篇文章中说到回归的损失函数为:
L=∑n(y^n−(b+∑wixin))2θi=θi−1−η∇L(θi−1)
L = \sum_{n}(\hat{y}^n -(b + \sum w_ix_i^n))^2 \\
\theta^i = \theta^{i-1} - \eta\nabla L(\theta^{i-1})
L=n∑(y^n−(b+∑wixin))2θi=θi−1−η∇L(θi−1)
损失考虑了所有的训练数据。
而随机梯度下降法,每次只取某一个训练数据xnx^nxn出来:
而损失值只考虑现在的参数对该训练数据的的估测值减去实际值:
Ln=(y^n−(b+∑wixin))2θi=θi−1−η∇Ln(θi−1) L^n = (\hat{y}^n -(b + \sum w_ix_i^n))^2 \\ \theta^i = \theta^{i-1} - \eta\nabla L^n(\theta^{i-1}) Ln=(y^n−(b+∑wixin))2θi=θi−1−η∇Ln(θi−1)
并且计算梯度的时候也只计算只针对该训练数据xnx^nxn计算。

左边看完20个训练数据才更新损失值,右边每看一个训练数据,就更新一次损失值。
特征缩放
假设要根据以下函数做回归
y=b+w1x1+w2x2y = b + w_1x_1 + w_2x_2y=b+w1x1+w2x2
假设x2x_2x2的分布比x1x_1x1要大,就需要把x2x_2x2的分布缩小,让它们一致。

举例来说

如果x1x_1x1的分布是1,2,… 而 x2x_2x2的分布是 100,200,…
那么画出的损失值的图形是图左的样子;
如果进行缩放后,图形是正圆,很容易向着圆心走。可以极大提高算法的效率。
特征缩放的方法
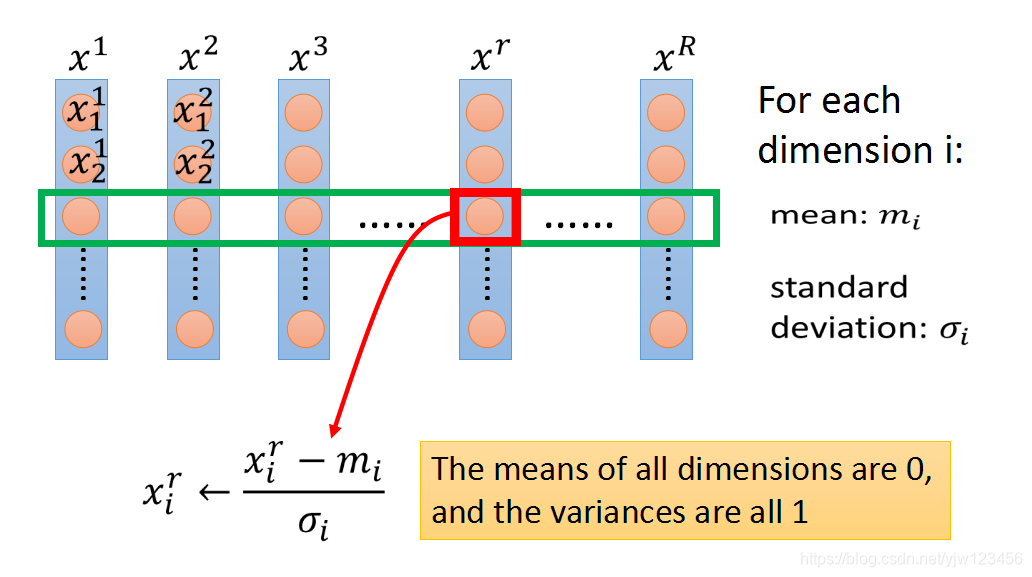
对每个维度,计算该维度的均值mi=∑xirRm_i = \frac{\sum x^r_i}{R}mi=R∑xir和标准差σi=∑(xir−mi)2R\sigma_i = \sqrt{\frac{\sum(x_i^r-m_i)^2}{R}}σi=R∑(xir−mi)2
- 点赞
- 收藏
- 分享
- 文章举报
 愤怒的可乐
博客专家
发布了151 篇原创文章 · 获赞 186 · 访问量 14万+
私信
关注
愤怒的可乐
博客专家
发布了151 篇原创文章 · 获赞 186 · 访问量 14万+
私信
关注
- 3、【李宏毅机器学习(2017)】Gradient Descent(梯度下降)
- 机器学习 :李宏毅:线性回归 梯度下降:(goodness of function)
- 机器学习 李宏毅 L6-梯度下降法
- Machine Learning(Stanford)| 斯坦福大学机器学习笔记--第一周(4.梯度下降)
- [机器学习] Coursera ML笔记 - 神经网络(Learning) - 标准梯度下降
- 机器学习小组知识点4:批量梯度下降法(BGD)
- 理解梯度下降在机器学习模型优化中的应用
- 机器学习系列(1):线性回归(regression)和梯度下降(gradient descent)
- 为什么一些机器学习模型需要对数据进行归一化?——1)归一化后加快了梯度下降求最优解的速度;2)归一化有可能提高精度
- 机器学习中的数学知识(-)梯度下降数学理论
- 斯坦福机器学习3:线性回归、梯度下降和正规方程组的matlab实现
- 机器学习_1.3(线性回归之梯度下降+总结)
- 【机器学习入门】Andrew NG《Machine Learning》课程笔记之二 :基本概念、代价函数、梯度下降和线性回归
- 机器学习入门:线性回归及梯度下降
- python机器学习第二章(3)改善梯度下降
- 机器学习中的数学-线性回归和梯度下降
- 机器学习(六)梯度下降的优化算法和matlab/octave中的应用
- 【机器学习】梯度下降(Gradient Descent)小结
- 斯坦福大学公开课机器学习课程(Andrew Ng)二监督学习应用 梯度下降
- 机器学习3- 梯度下降(Gradient Descent)
