分类

x -> function -> Class n

分类问题就是要找到一个函数使得给定输入能输出它所属的类别。

又以宝可梦为例，宝可梦有十八种属性：电、火等

比如输入是皮卡丘输出就是电。

如何分类

首先要收集训练数据

在二元分类模型（只有两个类别）中：

输入x,g(x) > 0 则 class1 否则 class2

那么损失函数可以这样定义：

L(f)=∑nδ(f(xn)≠y^n) L(f) = \sum_n \delta(f(x^n) ≠ \hat y^n) L(f)=n∑​δ(f(xn)​=y^​n)
也就是它的错误次数，越小说明这个函数越好。

下面通过概率论的知识来解决找到最好的函数问题。

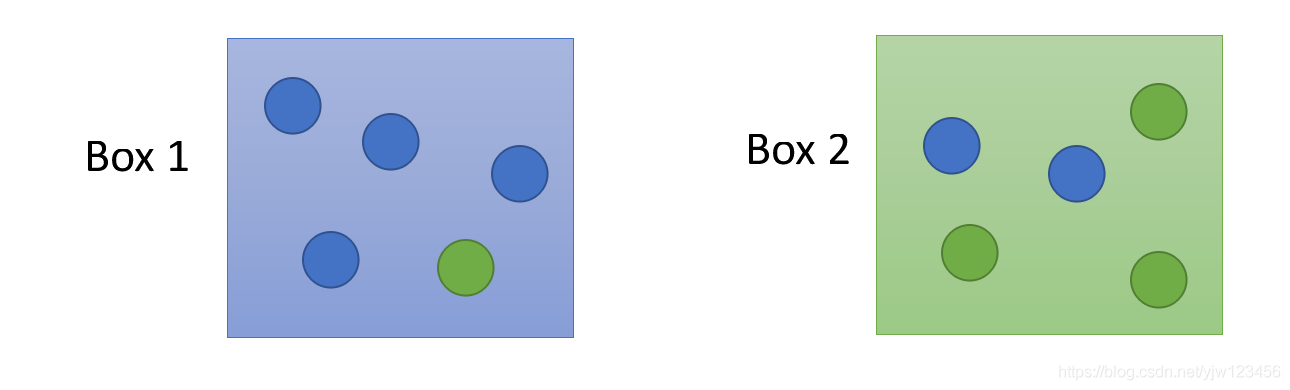
给定两个盒子，从这两个盒子中随机抽一个球出来，它是蓝色的。
那么这蓝色的球从盒子1和盒子2中抽出来的几率分别是多少？

假设从盒子1中抽球的概率 P(B1)=2/3P(B_1)= 2/3P(B1​)=2/3,从盒子2中抽球的概率P(B2)=1/3P(B_2)=1/3P(B2​)=1/3

并且盒子1里面蓝球的概率是P(Blue∣B1)=4/5P(Blue|B_1)=4/5P(Blue∣B1​)=4/5,绿球的概率是P(Green∣B1)=1/5P(Green|B_1)=1/5P(Green∣B1​)=1/5
盒子2中蓝球的概率是P(Blue∣B2)=2/5P(Blue|B_2)=2/5P(Blue∣B2​)=2/5，绿球的概率是P(Green∣B2)=3/5P(Green|B_2)=3/5P(Green∣B2​)=3/5

那么根据贝叶斯公式，可以计算出蓝球从盒子1中抽出来的概率是:

P(B1∣Blue)=P(Blue∣B1)P(B1)P(Blue∣B1)P(B1)+P(Blue∣B2)P(B2) P(B_1|Blue) = \frac{P(Blue|B_1)P(B_1)}{P(Blue|B_1)P(B_1)+P(Blue|B_2)P(B_2)} P(B1​∣Blue)=P(Blue∣B1​)P(B1​)+P(Blue∣B2​)P(B2​)P(Blue∣B1​)P(B1​)​

现在把盒子换成类别的话：

假设有两个类别Class1和Class2。

给定一个x,那么它属于哪个类别呢？
如果知道从Class1中抽x的概率P(C1)P(C_1)P(C1​)和从Class2中抽x的概率P(C2)P(C_2)P(C2​)；

从Class1中抽到x的概率P(x∣C1)P(x|C_1)P(x∣C1​)以及从Class2中抽到x的概率P(x∣C2)P(x|C_2)P(x∣C2​)

那么可以计算x属于Class1的概率有多大：

P(C1∣x)=P(x∣C1)P(C1)P(x∣C1)P(C1)+P(x∣C2)P(C2) P(C_1|x) = \frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)} P(C1​∣x)=P(x∣C1​)P(C1​)+P(x∣C2​)P(C2​)P(x∣C1​)P(C1​)​

这就叫做生成模型(Generative Mode)。顾名思义，有了这个模型，这可以用来生成x。

可以计算某一个x出现的几率P(x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)P(x)=P(x|C_1)P(C_1) +P(x|C_2)P(C_2)P(x)=P(x∣C1​)P(C1​)+P(x∣C2​)P(C2​)，就可以知道x的分布，然后就可以用这个分布来生成x。

假设我们考虑水系(Water)和一般系(Normal)的神奇宝贝。

在训练数据中，共有79只水系的，61只一般系的。

那从Class1中取得一只宝可梦的几率是P(C1)=79/(79+61)=0.56P(C_1)=79/(79+61)=0.56P(C1​)=79/(79+61)=0.56；
那从Class2中取得一只宝可梦的几率是P(C1)=61/(79+61)=0.44=1−P(C1)P(C_1)=61/(79+61)=0.44 = 1 - P(C_1)P(C1​)=61/(79+61)=0.44=1−P(C1​)；

那么从水系的神奇宝贝中挑出一只是海龟的几率(P(海龟∣Water)P(海龟|Water)P(海龟∣Water))有多大？

也就是P(x∣C1)=?P(x|C_1) = ?P(x∣C1​)=?

我们知道每个神奇宝贝都是用特征(feature)向量来描述。

我们首先考虑防御力(Defense)和特殊防御力(SP Defense)这两个特征(因为没法画出7个特征的图像出来…)

每个点都代表一只宝可梦，如果给我们一个不在训练数据中的新的神奇宝贝，比如海龟。

那么从水系中挑出一只神奇宝贝是海龟的几率是多少？ P(x∣Water)=?P(x|Water) = ?P(x∣Water)=?

可以想象这79只神奇宝贝是从某个高斯分布(正态分布)中取样出来，那么找到海龟代表的那个点的几率就不是0。

那给定这79个点，怎么找到这个高斯分布。

高斯分布常见的形式是：

f(x;μ,σ)=12πσexp−(x−μ)22σ2 f(x;\mu,\sigma)=\frac{1}{\sqrt{2\pi}\sigma}exp^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x;μ,σ)=2π​σ1​exp−2σ2(x−μ)2​

视频中给出了另一个种形式：

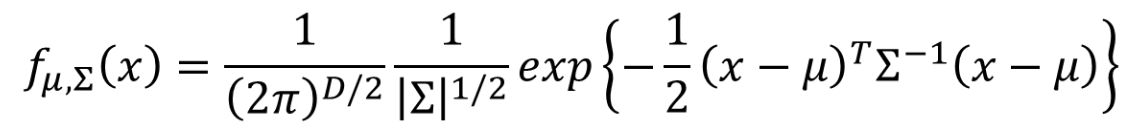
可以把高斯分布想成一个函数，这个函数的输入就是向量x，代表某只宝可梦的数值；
输出就是这只宝可梦从这个分布中取样出来的几率。

这个几率由均值μ\muμ和协方差矩阵Σ\SigmaΣ组成。

把不同的μ\muμ和Σ\SigmaΣ代入这个函数，就能得到不同的图像，x的几率也不一样。

同样的Σ\SigmaΣ不同的μ\muμ得出来的图形中几率分布最高点的位置不一样；

同样的μ\muμ和不同的Σ\SigmaΣ的几率分布最高点位置一样，但是分布发散的程度不一样。

假设有一个高斯分布存在，从这个分布中取样79次后，取出这79个点。

那么这个高斯分布到底是什么样的呢？

假设我们可以根据这个79个点估测出高斯分布的μ\muμ和Σ\SigmaΣ。

接着给一个新的点x，它不在我们过去所见过的79个点里面，我们已经知道了μ\muμ和Σ\SigmaΣ，我们就可以写出高斯函数

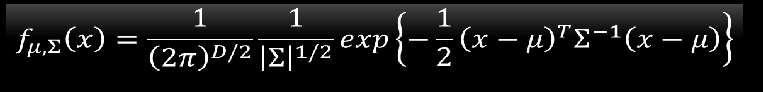
然后把x代进去，就可以算出这个x从这个分布出取样出来的几率，如果x越接近中心点，那么取样出来的概率就越大。

那么现在的问题就是如何找到这个μ\muμ和Σ\SigmaΣ，用的方法是极大似然。

极大似然

可以想象这个79个点能从任何μ\muμ 和 Σ\SigmaΣ 的高斯分布中生成出来。

从高斯分布中生成能生成任何一个点，不过几率有高低之别。

如上图，左下角那个分布生成这个79个点的可能性(Likelihood)比右上角的分布要高。

所以给定μ\muμ和Σ\SigmaΣ，就可以算出生成这些点的可能性 就是取样出每个点的几率之积:

L(μ,Σ)=fμ,Σ(x1)fμ,Σ(x2)fμ,Σ(x3)⋯fμ,Σ(x79) L(\mu,\Sigma) = f_{\mu,\Sigma}(x^1)f_{\mu,\Sigma}(x^2)f_{\mu,\Sigma}(x^3)\cdots f_{\mu,\Sigma}(x^{79}) L(μ,Σ)=fμ,Σ​(x1)fμ,Σ​(x2)fμ,Σ​(x3)⋯fμ,Σ​(x79)

上面的LLL不是代表损失函数，而是取Likelihood中的首字母。

所以，接下来要做的事情是找到生成这个79个点可能性最大(maximum likelihood)的高斯分布((μ∗,Σ∗)(\mu^*,\Sigma^*)(μ∗,Σ∗))。

μ∗,Σ∗=arg max⁡μ,ΣL(μ,Σ) \mu^*,\Sigma^*=arg\,\max_{\mu,\Sigma}L(\mu,\Sigma) μ∗,Σ∗=argμ,Σmax​L(μ,Σ)

我们可以穷举所有的μ\muμ和Σ\SigmaΣ，找到使上面式子结果最大。

平均就是μ∗\mu^*μ∗

μ∗=179∑n=179xn \mu^* = \frac{1}{79} \sum_{n=1}^{79} x^n μ∗=791​n=1∑79​xn
而Σ∗\Sigma^*Σ∗是

Σ∗=179∑n=179(xn−μ∗)(xn−μ∗)T \Sigma^* = \frac{1}{79} \sum_{n=1}^{79} (x^n - \mu^*)(x^n - \mu^*)^T Σ∗=791​n=1∑79​(xn−μ∗)(xn−μ∗)T

然后根据上面的公式算出来两个类别的μ\muμ和Σ\SigmaΣ:

现在我们就可以进行分类了!
我们只要算出P(C1∣x)P(C_1|x)P(C1​∣x)的几率，根据下式：

P(C1∣x)=P(x∣C1)P(C1)P(x∣C1)P(C1)+P(x∣C2)P(C2) P(C_1|x) = \frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)} P(C1​∣x)=P(x∣C1​)P(C1​)+P(x∣C2​)P(C2​)P(x∣C1​)P(C1​)​

如果P(C1∣x)>0.5P(C_1|x) > 0.5P(C1​∣x)>0.5，那么x就属于类别1(水系)。

我们已知了P(C1)P(C_1)P(C1​)和P(C2)P(C_2)P(C2​)，然后代入μ1\mu^1μ1和Σ1\Sigma^1Σ1得出P(x∣C1)P(x|C_1)P(x∣C1​)的值，同理可得出P(x∣C2)P(x|C_2)P(x∣C2​)的值，整个式子的结果就可以计算出来了。

那结果怎样？

蓝色的点是水系的神奇宝贝的分布，红点时一般系的分布。

红色区域几率大于0.5是类别1；蓝色区间几率小于0.5，是类别2。

然后把这个模型用于测试数据，发现正确率只有47%，但此时我们只考虑了两个特征。

我们把所有特征都考虑进来（共7个），结果准确率也只有54%。
上面得出的分类结果不太好，我们优化一下模型，让两个类别共用同一个Σ\SigmaΣ。

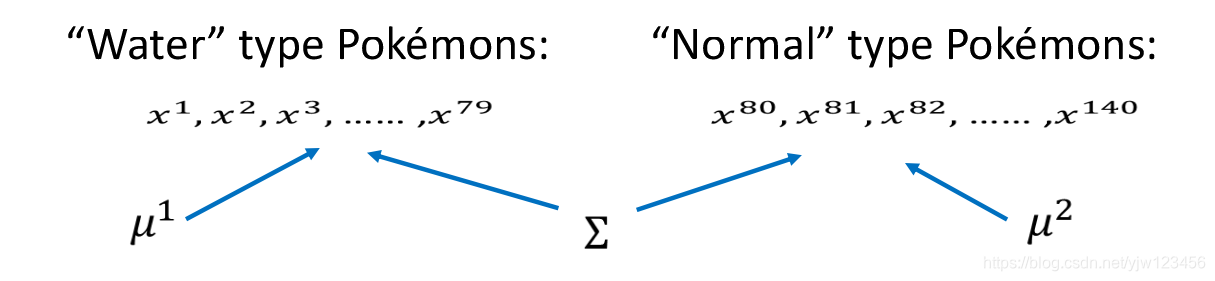
假设水系79个神奇宝贝是从μ1,Σ\mu^1,\Sigmaμ1,Σ的高斯分布生成出来的，同时另外61只（编号从80开始）神奇宝贝从μ2,Σ\mu^2,\Sigmaμ2,Σ的高斯分布生成出来，这两个分布的协方差矩阵是同一个。

那该怎么计算最大似然呢？

L(μ1,μ2,Σ)=fμ1,Σ(x1)fμ1,Σ(x2)fμ1,Σ(x3)⋯fμ1,Σ(x79)×fμ2,Σ(x80)fμ2,Σ(x81)fμ2,Σ(x82)⋯fμ2,Σ(x140) L(\mu^1,\mu^2,\Sigma) = f_{\mu^1,\Sigma}(x^1)f_{\mu^1,\Sigma}(x^2)f_{\mu^1,\Sigma}(x^3)\cdots f_{\mu^1,\Sigma}(x^{79}) \\ \times f_{\mu^2,\Sigma}(x^{80})f_{\mu^2,\Sigma}(x^{81})f_{\mu^2,\Sigma}(x^{82})\cdots f_{\mu^2,\Sigma}(x^{140}) L(μ1,μ2,Σ)=fμ1,Σ​(x1)fμ1,Σ​(x2)fμ1,Σ​(x3)⋯fμ1,Σ​(x79)×fμ2,Σ​(x80)fμ2,Σ​(x81)fμ2,Σ​(x82)⋯fμ2,Σ​(x140)

用μ1,Σ\mu^1,\Sigmaμ1,Σ产生x1x^1x1到x79x^{79}x79，用μ2,Σ\mu^2,\Sigmaμ2,Σ产生x80x^{80}x80到x140x^{140}x140

μ1\mu^1μ1和μ2\mu^2μ2的计算方法和前面的相同。

而Σ\SigmaΣ的取值为

Σ=79140Σ1+61140Σ2 \Sigma = \frac{79}{140}\Sigma^1 + \frac{61}{140}\Sigma^2 Σ=14079​Σ1+14061​Σ2

然后再看一下结果，看有什么改进没

在考虑了所有特征的情况下，准确率到了73%，右边的模型也称为线性模型。

总结一下上面的步骤

如果所有特征(维度)都是独立的，那么你可以尝试使用朴素贝叶斯分类器。

Sigmoid 函数

P(C1∣x)=P(x∣C1)P(C1)P(x∣C1)P(C1)+P(x∣C2)P(C2) P(C_1 | x ) = \frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1) + P(x|C_2)P(C_2)} P(C1​∣x)=P(x∣C1​)P(C1​)+P(x∣C2​)P(C2​)P(x∣C1​)P(C1​)​

我们来整理下这个式子，上下同除分子，得到：

11+P(x∣C2)P(C2)P(x∣C1)P(C1) \frac{1}{1 + \frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}} 1+P(x∣C1​)P(C1​)P(x∣C2​)P(C2​)​1​
令 z=lnP(x∣C1)P(C1)P(x∣C2)P(C2)z = ln \frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}z=lnP(x∣C2​)P(C2​)P(x∣C1​)P(C1​)​

因为ln1x=lnx−1=−lnxln \frac{1}{x} = ln x^{-1} = - ln xlnx1​=lnx−1=−lnx 以及 elnx=xe ^ {ln x} = xelnx=x

所以就有上式等于:

11+e−z=σ(z) \frac{1}{1 + e ^{-z}} = \sigma (z) 1+e−z1​=σ(z)

这个函数叫做Sigmoid函数，它的图形为：

接下来算一下zzz应该是怎样的 z=lnP(x∣C1)P(C1)P(x∣C2)P(C2)z = ln \frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}z=lnP(x∣C2​)P(C2​)P(x∣C1​)P(C1​)​

P(C1∣x)=σ(z),  z=lnP(x∣C1)P(C1)P(x∣C2)P(C2) P(C_1|x)=\sigma(z),\,\,z = ln \frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)} \\ P(C1​∣x)=σ(z),z=lnP(x∣C2​)P(C2​)P(x∣C1​)P(C1​)​
把相乘的部分变成相加得

z=lnP(x∣C1)P(x∣C2)+lnP(C1)P(C2) z = ln \frac{P(x|C_1)}{P(x|C_2)} + ln \frac{P(C_1)}{P(C_2)} z=lnP(x∣C2​)P(x∣C1​)​+lnP(C2​)P(C1​)​

而

P(C1)P(C2)=N1N1+N2N2N1+N2=N1N2 \frac{P(C_1)}{P(C_2)} = \frac{\frac{N_1}{N_1 + N_2}}{\frac{N_2}{N_1 + N_2}} = \frac{N_1}{N_2} P(C2​)P(C1​)​=N1​+N2​N2​​N1​+N2​N1​​​=N2​N1​​

N1N_1N1​代表Class1在训练数据集中出现的次数，N2N_2N2​代表Class2在训练集中出现的次数。

而

P(X∣C1)=1(2π)D/21∣Σ1∣1/2exp{−12(x−μ1)T(Σ1)−1(x−μ1)} P(X|C_1) = \frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma^1|^{1/2}}exp\{-\frac{1}{2}(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)\} P(X∣C1​)=(2π)D/21​∣Σ1∣1/21​exp{−21​(x−μ1)T(Σ1)−1(x−μ1)}

P(X∣C2)=1(2π)D/21∣Σ2∣1/2exp{−12(x−μ2)T(Σ2)−1(x−μ2)} P(X|C_2) = \frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma^2|^{1/2}}exp\{-\frac{1}{2}(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)\} P(X∣C2​)=(2π)D/21​∣Σ2∣1/21​exp{−21​(x−μ2)T(Σ2)−1(x−μ2)}

lnP(x∣C1)P(x∣C2)=ln1(2π)D/21∣Σ1∣1/2exp{−12(x−μ1)T(Σ1)−1(x−μ1)}1(2π)D/21∣Σ2∣1/2exp{−12(x−μ2)T(Σ2)−1(x−μ2)}=ln∣Σ2∣1/2∣Σ1∣1/2exp{−12[(x−μ1)T(Σ1)−1(x−μ1)−(x−μ2)T(Σ2)−1(x−μ2)]}=ln∣Σ2∣1/2∣Σ1∣1/2−12[(x−μ1)T(Σ1)−1(x−μ1)−(x−μ2)T(Σ2)−1(x−μ2)] \begin{aligned} ln \frac{P(x|C_1)}{P(x|C_2)} &= ln \frac{\bcancel{\frac{1}{(2\pi)^{D/2}}} \frac{1}{|\Sigma^1|^{1/2}}exp\{-\frac{1}{2}(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)\}} {\bcancel{\frac{1}{(2\pi)^{D/2}}} \frac{1}{|\Sigma^2|^{1/2}}exp\{-\frac{1}{2}(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)\}} \\ &= ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} exp\{-\frac{1}{2}[(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1) - (x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)]\} \\ &= ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} - \frac{1}{2}[(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1) - (x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)] \end{aligned} lnP(x∣C2​)P(x∣C1​)​​=ln(2π)D/21​​∣Σ2∣1/21​exp{−21​(x−μ2)T(Σ2)−1(x−μ2)}(2π)D/21​​∣Σ1∣1/21​exp{−21​(x−μ1)T(Σ1)−1(x−μ1)}​=ln∣Σ1∣1/2∣Σ2∣1/2​exp{−21​[(x−μ1)T(Σ1)−1(x−μ1)−(x−μ2)T(Σ2)−1(x−μ2)]}=ln∣Σ1∣1/2∣Σ2∣1/2​−21​[(x−μ1)T(Σ1)−1(x−μ1)−(x−μ2)T(Σ2)−1(x−μ2)]​
接下来把(x−μ1)T(Σ1)−1(x−μ1)(x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1)(x−μ1)T(Σ1)−1(x−μ1)展开

(x−μ1)T(Σ1)−1(x−μ1)=xT(Σ1)−1x−xT(Σ1)μ1−(μ1)T(Σ1)−1x+(μ1)T(Σ1)−1μ1=xT(Σ1)−1x−2(μ1)T(Σ1)−1x+(μ1)T(Σ1)−1μ1 \begin{aligned} (x-\mu^1)^T(\Sigma^1)^{-1}(x-\mu^1) &= x^T(\Sigma^1)^{-1}x - x^T(\Sigma^1)\mu^1 - (\mu^1)^T(\Sigma^1)^{-1}x + (\mu^1)^T(\Sigma^1)^{-1}\mu^1 \\ &= x^T(\Sigma^1)^{-1}x - 2(\mu^1)^T(\Sigma^1)^{-1}x + (\mu^1)^T(\Sigma^1)^{-1}\mu^1 \end{aligned} (x−μ1)T(Σ1)−1(x−μ1)​=xT(Σ1)−1x−xT(Σ1)μ1−(μ1)T(Σ1)−1x+(μ1)T(Σ1)−1μ1=xT(Σ1)−1x−2(μ1)T(Σ1)−1x+(μ1)T(Σ1)−1μ1​

(x−μ2)T(Σ2)−1(x−μ2)(x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2)(x−μ2)T(Σ2)−1(x−μ2)展开：

(x−μ2)T(Σ2)−1(x−μ2)=xT(Σ2)−1x−2(μ2)T(Σ2)−1x+(μ2)T(Σ2)−1μ2 \begin{aligned} (x-\mu^2)^T(\Sigma^2)^{-1}(x-\mu^2) &= x^T(\Sigma^2)^{-1}x - 2(\mu^2)^T(\Sigma^2)^{-1}x + (\mu^2)^T(\Sigma^2)^{-1}\mu^2 \end{aligned} (x−μ2)T(Σ2)−1(x−μ2)​=xT(Σ2)−1x−2(μ2)T(Σ2)−1x+(μ2)T(Σ2)−1μ2​

所以zzz可以写成：

z=ln∣Σ2∣1/2∣Σ1∣1/2−12xT(Σ1)−1x+(μ1)T(Σ1)−1x−12(μ1)T(Σ1)−1μ1+12xT(Σ2)−1x−(μ2)T(Σ2)−1x+12(μ2)T(Σ2)−1μ2+lnN1N2 \begin{aligned} z &= ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}} - \frac{1}{2} x^T(\Sigma^1)^{-1}x + (\mu^1)^T(\Sigma^1)^{-1}x - \frac{1}{2} (\mu^1)^T(\Sigma^1)^{-1}\mu^1 \\ &+ \frac{1}{2}x^T(\Sigma^2)^{-1}x -(\mu^2)^T(\Sigma^2)^{-1}x + \frac{1}{2} (\mu^2)^T(\Sigma^2)^{-1}\mu^2 + ln \frac{N_1}{N_2} \end{aligned} z​=ln∣Σ1∣1/2∣Σ2∣1/2​−21​xT(Σ1)−1x+(μ1)T(Σ1)−1x−21​(μ1)T(Σ1)−1μ1+21​xT(Σ2)−1x−(μ2)T(Σ2)−1x+21​(μ2)T(Σ2)−1μ2+lnN2​N1​​​

而我们上面说过,如果共用Σ\SigmaΣ的话，那么就有Σ1=Σ2=Σ\Sigma_1 = \Sigma_2 = \SigmaΣ1​=Σ2​=Σ

那么上式有：

z=ln∣Σ2∣1/2∣Σ1∣1/2−12xT(Σ1)−1x+(μ1)T(Σ1)−1x−12(μ1)T(Σ1)−1μ1+12xT(Σ2)−1x−(μ2)T(Σ2)−1x+12(μ2)T(Σ2)−1μ2+lnN1N2=(μ1−μ2)TΣ−1x−12(μ1)T(Σ1)−1+12(μ2)T(Σ2)−1μ2+lnN1N2 \begin{aligned} z &= \bcancel{ln \frac{|\Sigma^2|^{1/2}}{|\Sigma^1|^{1/2}}} - \cancel{\frac{1}{2} x^T(\Sigma^1)^{-1}x} + (\mu^1)^T(\Sigma^1)^{-1}x - \frac{1}{2} (\mu^1)^T(\Sigma^1)^{-1}\mu^1 \\ &+ \cancel{\frac{1}{2}x^T(\Sigma^2)^{-1}x} -(\mu^2)^T(\Sigma^2)^{-1}x + \frac{1}{2} (\mu^2)^T(\Sigma^2)^{-1}\mu^2 + ln \frac{N_1}{N_2} \\ &= (\mu^1-\mu^2)^T\Sigma^{-1}x - \frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1} + \frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2 + ln \frac{N_1}{N_2} \end{aligned} z​=ln∣Σ1∣1/2∣Σ2∣1/2​​−21​xT(Σ1)−1x​+(μ1)T(Σ1)−1x−21​(μ1)T(Σ1)−1μ1+21​xT(Σ2)−1x​−(μ2)T(Σ2)−1x+21​(μ2)T(Σ2)−1μ2+lnN2​N1​​=(μ1−μ2)TΣ−1x−21​(μ1)T(Σ1)−1+21​(μ2)T(Σ2)−1μ2+lnN2​N1​​​

假设wT=(μ1−μ2)TΣ−1w^T = (\mu^1-\mu^2)^T\Sigma^{-1}wT=(μ1−μ2)TΣ−1 ，后面这一项其实就是一个常数，另b=−12(μ1)T(Σ1)−1+12(μ2)T(Σ2)−1μ2+lnN1N2b = - \frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1} + \frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2 + ln \frac{N_1}{N_2}b=−21​(μ1)T(Σ1)−1+21​(μ2)T(Σ2)−1μ2+lnN2​N1​​

因为P(C1∣x)=σ(z)P(C_1|x) = \sigma(z)P(C1​∣x)=σ(z)

而z=w⋅x+bz = w \cdot x + bz=w⋅x+b

也就有P(C1∣x)=σ(w⋅x+b)P(C_1|x) = \sigma(w \cdot x + b)P(C1​∣x)=σ(w⋅x+b)

它解释了为什么共用Σ\SigmaΣ时界线是线性的。

在生成模型中，我们找出N1,N2,μ1,μ2,ΣN_1,N_2,\mu^1,\mu^2,\SigmaN1​,N2​,μ1,μ2,Σ就可以代入上式，然后就能算出几率

但是为什么要这么麻烦呢？最终要找到一个向量www和一个常量bbb，如果我们能否直接找出www和bbb就好了。

• 点赞
• 收藏
• 分享
• 文章举报

愤怒的可乐 博客专家 发布了151 篇原创文章 · 获赞 186 · 访问量 14万+ 私信 关注