前言

本文只会记录人工智能中所用到的线性代数知识，并不会记录大学线性代数教材中的所有知识。
只会介绍向量和矩阵、特征向量和特征值以及矩阵分解。

标量

只有大小没有方向的量称为标量。

单个数字就是标量。

向量

所谓的向量就是一组数字，可以用vvv来表示
v=[123]v = \left[\begin{matrix}1 \\2 \\3 \end{matrix} \right]v=⎣⎡​123​⎦⎤​ 或 v=[1 2 3]v = [1 ~ 2 ~ 3]v=[1 2 3]

当两个向量大小相等、方向相同时，说这两个向量相等。

这里由3个数组成，叫做3维向量，相应的，由n个数组成的称为n维向量。

左边排成一列的形式叫做列向量；右边叫做行向量

viv_ivi​表示向量中的第iii个元素，本例中v1=1,v2=2,v3=3v_1 =1,v_2 = 2,v_3 = 3v1​=1,v2​=2,v3​=3

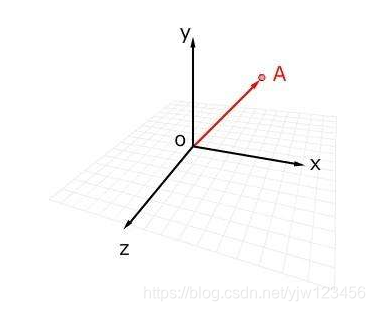
3维向量可以在3维空间中表示出来。

向量的长度

n维向量α=(a1,a2,...,an)\alpha = (a_1,a_2,...,a_n)α=(a1​,a2​,...,an​)，数值a12+a22+...+an2\sqrt{a_1^2 + a_2^2 + ... + a_n^2}a12​+a22​+...+an2​​称为向量α\alphaα的长度或模，记为∥α∥\left \| \alpha \right \|∥α∥

∥α∥=1\left \| \alpha \right \| = 1∥α∥=1 称α\alphaα为单位向量。

向量的运算

向量的加法：

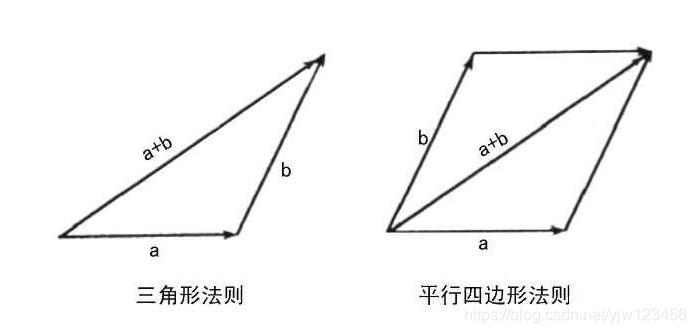
向量的减法：

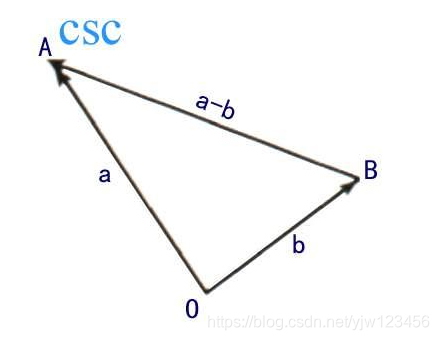
注意a⃗−b⃗\vec{a} - \vec{b}a−b得到的向量为b⃗\vec{b}b指向a⃗\vec{a}a。

向量的乘法：

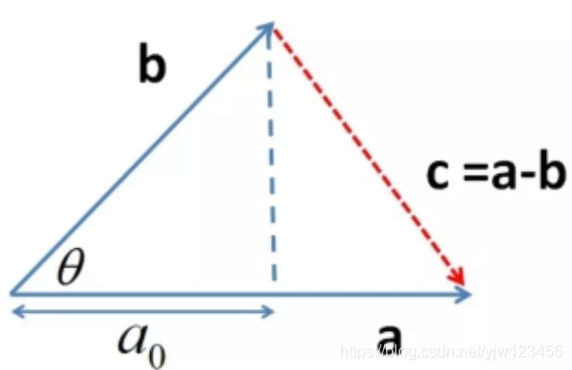
a⃗⋅b⃗=∣a⃗∣⋅∣b⃗∣cos⁡θ\vec{a} \cdot \vec{b} = | \vec{a} | \cdot |\vec{b}| \cos \thetaa⋅b=∣a∣⋅∣b∣cosθ

相当于向量b⃗\vec{b}b在向量a⃗\vec{a}a的方向的投影与向量∣a⃗∣| \vec{a} |∣a∣相乘

向量的范数

向量的1-范数： ∥X∥1=∣x1∣+∣x2∣+...+∣xn∣\left \| X \right \|_1 = |x_1| +|x_2| + ... + |x_n|∥X∥1​=∣x1​∣+∣x2​∣+...+∣xn​∣ ；各元素的绝对值之和
向量的2-范数： ∥X∥=x12+x22+...+xn2\left \| X \right \| = \sqrt{x_1^2 + x_2^2 + ... + x_n^2}∥X∥=x12​+x22​+...+xn2​​ ； 每个元素的平方和再开方，也就是n维向量的长度；
向量的无穷范数： ∥X∥∞=max⁡(∣x1∣,∣x2∣,...,∣xn∣)\left \| X \right \|_\infty = \max(|x_1|,|x_2|,...,|x_n|)∥X∥∞​=max(∣x1​∣,∣x2​∣,...,∣xn​∣) ；分量绝对值的最大者
向量的p-范数： ∥X∥p=(∑i=1n∣xi∣p)1p,(1≤p≤n)\left \| X \right \|_p = (\sum_{i=1}^n |x_i| ^ p)^{\frac{1}{p}} , (1 \leq p \leq n)∥X∥p​=(∑i=1n​∣xi​∣p)p1​,(1≤p≤n)

对于2-范数有： ∣∣x∣∣+∣∣y∣∣≥∣∣x+y∣∣||x|| + ||y|| \geq || x + y||∣∣x∣∣+∣∣y∣∣≥∣∣x+y∣∣

当 ∣∣x⃗∣∣||\vec{x}||∣∣x∣∣ ≠ 000 ，∣∣y⃗∣∣||\vec{y}||∣∣y​∣∣ ≠ 000 时，称
θ=arccos⁡a⃗⋅y⃗∣∣x⃗∣∣∣∣y⃗∣∣ \theta = \arccos \frac{ \vec{a} \cdot \vec{y}}{||\vec{x}|| || \vec{y}||} θ=arccos∣∣x∣∣∣∣y​∣∣a⋅y​​
为向量x⃗\vec{x}x与y⃗\vec{y}y​的夹角。

向量的内积

设有n维向量
x⃗=[x1x2⋮xn],y⃗=[y1y2⋮yn], \vec{x} = \left[ \begin{matrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{matrix} \right], \vec{y} = \left[ \begin{matrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{matrix} \right], x=⎣⎢⎢⎢⎡​x1​x2​⋮xn​​⎦⎥⎥⎥⎤​,y​=⎣⎢⎢⎢⎡​y1​y2​⋮yn​​⎦⎥⎥⎥⎤​,

令[x⃗,y⃗]=∑i=1nxiyi=x1y1+x2y2+⋯+xnyn[\vec{x},\vec{y}] = \sum_{i=1}^n x_i y_i = x_1y_1 + x_2y_2 + \cdots+ x_ny_n[x,y​]=∑i=1n​xi​yi​=x1​y1​+x2​y2​+⋯+xn​yn​
上式称为向量的内积，内积的结果是一个标量。

这里要求一维向量x⃗\vec{x}x和向量y⃗\vec{y}y​的行列数相同。

当[x⃗,y⃗]=0[\vec{x},\vec{y}] = 0[x,y​]=0时，称向量x⃗\vec{x}x和向量y⃗\vec{y}y​正交。

一组两两相交的非零向量，称为正交向量组。

向量组

若干个同维的列向量(行向量)所组成的集合称为向量组。
如a1⃗,a2⃗,a3⃗,⋯ ,an⃗\vec{a_1},\vec{a_2},\vec{a_3},\cdots,\vec{a_n}a1​​,a2​​,a3​​,⋯,an​​

[a11a21⋯am1a12a22⋯am2⋮⋮⋱⋮a1na2n⋯amn]\left[ \begin{matrix} a_{11} & a_{21} & \cdots & a_{m1}\\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{matrix} \right]⎣⎢⎢⎢⎡​a11​a12​⋮a1n​​a21​a22​⋮a2n​​⋯⋯⋱⋯​am1​am2​⋮amn​​⎦⎥⎥⎥⎤​

向量组的线性组合：
对于向量组a1⃗,a2⃗,a3⃗,⋯ ,an⃗\vec{a_1},\vec{a_2},\vec{a_3},\cdots,\vec{a_n}a1​​,a2​​,a3​​,⋯,an​​，如果有一组数k1,k2,⋯ ,knk_1,k_2,\cdots,k_nk1​,k2​,⋯,kn​，使
β⃗=k1a1⃗+k2a2⃗+⋯+knan⃗, \vec{\beta} = k_1 \vec{a_1} + k_2\vec{a_2} + \cdots + k_n\vec{a_n}, β​=k1​a1​​+k2​a2​​+⋯+kn​an​​,
则称向量β⃗\vec{\beta}β​是向量组a1⃗,a2⃗,a3⃗,⋯ ,an⃗\vec{a_1},\vec{a_2},\vec{a_3},\cdots,\vec{a_n}a1​​,a2​​,a3​​,⋯,an​​的一个线性组合，或称β⃗\vec{\beta}β​可由向量组a1⃗,a2⃗,a3⃗,⋯ ,an⃗\vec{a_1},\vec{a_2},\vec{a_3},\cdots,\vec{a_n}a1​​,a2​​,a3​​,⋯,an​​线性表示。

向量组的线性相关：

给定向量组A=a1⃗,a2⃗,a3⃗,⋯ ,an⃗A= \vec{a_1},\vec{a_2},\vec{a_3},\cdots,\vec{a_n}A=a1​​,a2​​,a3​​,⋯,an​​，如果存在不全为零的数k1,k2,⋯ ,knk_1,k_2,\cdots,k_nk1​,k2​,⋯,kn​使
k1a1⃗+k2a2⃗+⋯+knan⃗=0 k_1\vec{a_1} + k_2\vec{a_2} + \cdots + k_n\vec{a_n} = 0 k1​a1​​+k2​a2​​+⋯+kn​an​​=0

则称向量组AAA是线性相关的，否则称它为线性无关。

对于任一向量组，不是线性无关就是线性相关。

向量空间

设VVV是nnn维实向量构成的集合，对于向量的加法运算及数乘运算满足：

1. 任意α∈V,β∈V\alpha \in V,\beta \in Vα∈V,β∈V，有α+β∈V\alpha + \beta \in Vα+β∈V；
2. 任意α∈V,k∈R\alpha \in V, k \in Rα∈V,k∈R，有kα∈Vk\alpha \in Vkα∈V

则称集合VVV为RRR上的实向量空间，简称向量空间。

已知V1,V2V_1,V_2V1​,V2​是向量空间，若V1∈V2V_1 \in V_2V1​∈V2​，则称V1V_1V1​是V2V_2V2​的子空间。

向量空间的基

设VVV是一个向量空间，如果存在一组向量α1,α2,⋯ ,αr∈V\alpha_1,\alpha_2,\cdots,\alpha_r \in Vα1​,α2​,⋯,αr​∈V，满足：

1. α1,α2,⋯ ,αr\alpha_1,\alpha_2,\cdots,\alpha_rα1​,α2​,⋯,αr​线性无关；
2. VVV中任意一组向量都可以由该向量组线性表示，则称α1,α2,⋯ ,αr\alpha_1,\alpha_2,\cdots,\alpha_rα1​,α2​,⋯,αr​为向量空间VVV的一组基；

矩阵

矩阵是一个按照长方阵列排列的复数或实数集合。
由m×nm × nm×n个数组成的一个mmm行nnn列的矩形表格，组成矩阵的每一个数，均称为矩阵的元素。如图所示：

A=[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn]A = \left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{matrix} \right]A=⎣⎢⎢⎢⎡​a11​a21​⋮am1​​a12​a22​⋮am2​​⋯⋯⋱⋯​a1n​a2n​⋮amn​​⎦⎥⎥⎥⎤​

单位矩阵：从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0，如：

[100010001]\left[ \begin{matrix} 1 & 0 & 0\\ 0& 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right]⎣⎡​100​010​001​⎦⎤​

矩阵的基本运算

两个矩阵的行数和列数分别相等，称它们为同型矩阵。

加法

矩阵的加法只能在两个同型矩阵之间进行，两个矩阵相加时，对应元素进行相加。

如：

[123457]+[002213]=[1256610] \left[ \begin{matrix} 1 & 2 & 3\\ 4 & 5 & 7 \end{matrix} \right] + \left[ \begin{matrix} 0 & 0 & 2\\ 2 & 1 & 3 \end{matrix} \right] = \left[ \begin{matrix} 1 & 2 & 5\\ 6 & 6 & 10 \end{matrix} \right] [14​25​37​]+[02​01​23​]=[16​26​510​]

数乘

数λ\lambdaλ与矩阵AAA的乘积记作λA\lambda AλA或AλA\lambdaAλ，规定为

λA=Aλ=[λa11λa12⋯λa1nλa21λa22⋯λa2n⋮⋮⋱⋮λam1λam2⋯λamn]\lambda A = A\lambda = \left[ \begin{matrix} \lambda a_{11} & \lambda a_{12} & \cdots & \lambda a_{1n}\\ \lambda a_{21} & \lambda a_{22} & \cdots & \lambda a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \lambda a_{m1} & \lambda a_{m2} & \cdots & \lambda a_{mn} \end{matrix} \right]λA=Aλ=⎣⎢⎢⎢⎡​λa11​λa21​⋮λam1​​λa12​λa22​⋮λam2​​⋯⋯⋱⋯​λa1n​λa2n​⋮λamn​​⎦⎥⎥⎥⎤​

乘法

必须满足矩阵AAA的列数与矩阵BBB的行数相等，或者矩阵AAA的行数与矩阵BBB的列数相等。

记C=ABC=ABC=AB，矩阵CCC的第iii行第jjj列的元素等于矩阵AAA的第iii行的所有元素与矩阵BBB的第jjj列的对应元素的乘积之和，即：
Cij=∑k=1naikbkj C_{ij} = \sum_{k=1}^na_{ik}b_{kj} Cij​=k=1∑n​aik​bkj​
如：

[123]1×3[456]3×1=1×4+2×5+3×6=32\left[ \begin{matrix} 1 & 2 & 3 \end{matrix} \right] _{1×3} \left[ \begin{matrix} 4 \\ 5 \\6 \end{matrix} \right]_{3×1} = 1×4 + 2×5 + 3×6 =32[1​2​3​]1×3​⎣⎡​456​⎦⎤​3×1​=1×4+2×5+3×6=32

[123]3×1[456]1×3=[45681012121518]3×3\left[ \begin{matrix} 1 \\ 2 \\3 \end{matrix} \right]_{3×1} \left[ \begin{matrix} 4 & 5 & 6 \end{matrix} \right] _{1×3} = \left[ \begin{matrix} 4 & 5 & 6\\ 8 & 10 & 12\\12 & 15 & 18 \end{matrix} \right]_{3×3}⎣⎡​123​⎦⎤​3×1​[4​5​6​]1×3​=⎣⎡​4812​51015​61218​⎦⎤​3×3​

矩阵的乘法不满足交换律

转置

矩阵AAA的转置矩阵，记作ATA^TAT，是将AAA的行列互换后所得矩阵，如果AAA是一个m×nm ×nm×n阶矩阵，ATA^TAT是一个n×mn×mn×m阶矩阵。

A=[142536]AT=[123456]A = \left[ \begin{matrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{matrix} \right] A^T = \left[ \begin{matrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{matrix} \right]A=⎣⎡​123​456​⎦⎤​AT=[14​25​36​]

矩阵的转置的性质：

1. (AT)T=A(A^T)^T = A(AT)T=A
2. (A+B)T=AT+BT(A+B)^T = A^T +B^T(A+B)T=AT+BT
3. (λA)T=λAT(\lambda A)^T=\lambda A^T(λA)T=λAT
4. (AB)T=BTAT(AB)^T = B^TA^T(AB)T=BTAT

逆矩阵

设AAA为nnn阶方阵(n×nn×nn×n)，若存在nnn阶方阵BBB使得:AB=BA=EAB=BA=EAB=BA=E(单位矩阵)，则称AAA是可逆的且矩阵BBB是矩阵AAA的逆矩阵，记为A−1=BA^{-1} = BA−1=B

矩阵的秩

矩阵的秩等于行向量组或列向量组最大线性无关组所包含的向量的个数。(矩阵的所有不等于零的子式的最高阶数称为矩阵的秩)

矩阵的特征值和特征向量

设AAA是nnn阶矩阵，如果数λ\lambdaλ和nnn维非零列向量xxx使关系式
Ax=λx Ax = \lambda x Ax=λx
成立，λ\lambdaλ称为方阵AAA的特征值，非零向量xxx称为AAA的对应于特征值λ\lambdaλ的特征向量。

方阵AAA的特征值，就是使齐次线性方程组(A−λE)x=0(A-\lambda E)x = 0(A−λE)x=0有非零解的λ\lambdaλ值，
即满足方程∣A−λE∣=0|A-\lambda E |= 0∣A−λE∣=0的λ\lambdaλ都是矩阵AAA的特征值。

相似矩阵

设A,BA,BA,B都是nnn阶矩阵，若有可逆矩阵PPP，使
P−1AP=B, P^{-1}AP = B, P−1AP=B,
则称BBB是AAA的相似矩阵，或说矩阵AAA与BBB相似。

• 点赞 2
• 收藏
• 分享
• 文章举报

愤怒的可乐 博客专家 发布了151 篇原创文章 · 获赞 186 · 访问量 14万+ 私信 关注