您的位置：首页 > 其它

李宏毅机器学习——深度学习反向传播算法

2020-04-01 18:28 239 查看

引言

在神经网络中，为了更有效的计算梯度，需要用到反向传播算法。我们先从链式求导法则开始。

链式求导法

先介绍下链式求导法则，在后面的反向传播算法中会用到。

有y=g(x),z=h(y)y = g(x),z=h(y)y=g(x),z=h(y)

那么dzdx=dzdydydx\frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx}dxdz=dydzdxdy;

有x=g(s),y=h(s),z=k(x,y)x=g(s) ,y = h(s), z = k(x,y)x=g(s),y=h(s),z=k(x,y)

改变了s会改变x和y，从而改变了z。

dzds=∂z∂xdxds+∂z∂ydyds\frac{dz}{ds} = \frac{\partial{z}}{\partial{x}}\frac{dx}{ds} + \frac{\partial{z}}{\partial{y}}\frac{dy}{ds}dsdz=∂x∂zdsdx+∂y∂zdsdy

注意，如果改变s会改变多个变量，它们的关系也是成立的。

损失函数

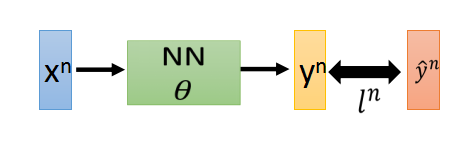
假设给定一组参数θ\thetaθ,把一个训练数据xnx^nxn代入NN(神经网络)中，会得到输出yny^nyn。

CnC^nCn是输出yny^nyn和实际y^n\hat{y}^ny^n距离函数，值越大代表越距离远，也就是效果越不好。

那在神经网络训练算法中，损失函数定义为：

L(θ)=∑n=1NCn(θ) L(\theta) = \sum^{N}_{n=1}C^n(\theta) L(θ)=n=1∑NCn(θ)

如果把损失函数对参数www做微分的话，得到

∂L(θ)∂w=∑n=1N∂Cn(θ)∂w \frac{\partial L(\theta)}{\partial w} = \sum^{N}_{n=1}\frac{\partial C^n(\theta)}{\partial w} ∂w∂L(θ)=n=1∑N∂w∂Cn(θ)

只要计算出某一笔数据对www的微分，就可以得到L(θ)L(\theta)L(θ)对www的微分。

假设我们先考虑这个神经元。

假设只有两个输入x1,x2x_1,x_2x1,x2，计算z=x1w1+x2w2+bz = x_1w_1 + x_2w_2 + bz=x1w1+x2w2+b得到zzz后再代入激活函数，经过多次运算会得到最终的输出y1,y2y_1,y_2y1,y2。

现在问题是如何计算损失(距离函数)CCC对www的偏微分∂C∂w\frac{\partial C}{\partial w}∂w∂C

利用链式求导法

∂C∂w=∂C∂z∂z∂w \frac{\partial C}{\partial w} = \frac{\partial C}{\partial z} \frac{\partial z}{\partial w} ∂w∂C=∂z∂C∂w∂z

计算∂z∂w\frac{\partial z}{\partial w}∂w∂z的过程叫做正向过程(Forward pass)；计算∂C∂z\frac{\partial C}{\partial z}∂z∂C的过程叫做反向过程(Backward pass)。

正向过程

z=x1w1+x2w2+bz = x_1w_1 + x_2w_2 + bz=x1w1+x2w2+b

∂z∂w1=x1∂z∂w2=x2 \frac{\partial z}{\partial w_1} = x_1 \\ \frac{\partial z}{\partial w_2} = x_2 \\ ∂w1∂z=x1∂w2∂z=x2

如上图所示，假设输入是1,−11,-11,−1，上面蓝色神经元的参数：w1=1,w2=−2,b=1w_1=1,w_2=-2,b=1w1=1,w2=−2,b=1，激活函数是

Sigmoid

函数；
下面蓝色神经元的参数：w1=−1,w2=1,b=0w_1=-1,w_2=1,b=0w1=−1,w2=1,b=0

对下面的神经元来说，计算w2w_2w2的偏微分，可以很快得出∂z∂w=−1\frac{\partial z}{\partial w} = -1∂w∂z=−1，也就是输入x2(−1)x_2(-1)x2(−1),随着从前往后计算每个神经元的输出，整个过程就可以很快结束，因此叫正向过程。

反向过程

困难的是如何计算∂C∂z\frac{\partial C}{\partial z}∂z∂C

a=11+e−za = \frac{1}{1+e^{-z}}a=1+e−z1

假设激活函数是

Sigmoid

函数a=σ(z)a=\sigma(z)a=σ(z)，然后得到的函数值aaa会乘上某个权重(比如w3w_3w3)再加上其他值得到z′z^\primez′(注意这里只是一个符号，不是zzz的导数)；aaa也会乘上权重(比如w4w_4w4)再加上其他东西得到z′′z^{\prime\prime}z′′(注意这里只是一个符号，不是zzz的二阶导数)；

∂C∂z=∂C∂a∂a∂z \frac{\partial C}{\partial z} = \frac{\partial C}{\partial a} \frac{\partial a}{\partial z} ∂z∂C=∂a∂C∂z∂a

可以这样理解，zzz通过影响aaa来影响CCC。

而

∂a∂z=∂σ(z)∂z=σ′(z) \frac{\partial a}{\partial z} = \frac{\partial \sigma(z)}{\partial z} = \sigma^\prime(z) ∂z∂a=∂z∂σ(z)=σ′(z)

那就剩下

∂C∂a=∂C∂z′∂z′∂a+∂C∂z′′∂z′′∂a \frac{\partial C}{\partial a} = \frac{\partial C}{\partial z^\prime}\frac{\partial z^\prime}{\partial a} + \frac{\partial C}{\partial z^{\prime\prime}}\frac{\partial z^{\prime\prime}}{\partial a} ∂a∂C=∂z′∂C∂a∂z′+∂z′′∂C∂a∂z′′

改变了aaa会改变z′z^{\prime}z′和z′′z^{\prime\prime}z′′，从而改变了CCC

我们先计算简单的

z′=aw3+⋯z^{\prime} = aw_3 + \cdotsz′=aw3+⋯

有
∂z′∂a=w3\frac{\partial z^{\prime}}{\partial a} = w_3∂a∂z′=w3

同理

∂z′′∂a=w4\frac{\partial z^{\prime\prime}}{\partial a} = w_4∂a∂z′′=w4

现在难点就是∂C∂z′\frac{\partial C}{\partial z^\prime}∂z′∂C和∂C∂z′′\frac{\partial C}{\partial z^{\prime\prime}}∂z′′∂C

我们这里先假装我们知道这两项的值。然后整理下原来的式子:

∂C∂z=σ′(z)[w3∂C∂z′+w4∂C∂z′′] \frac{\partial C}{\partial z} = \sigma^\prime(z)[w_3\frac{\partial C}{\partial z^\prime} + w_4\frac{\partial C}{\partial z^{\prime\prime}}] ∂z∂C=σ′(z)[w3∂z′∂C+w4∂z′′∂C]

假设有另外一个特殊的神经元，它是上图的样子，输入就是∂C∂z′\frac{\partial C}{\partial z^\prime}∂z′∂C和∂C∂z′′\frac{\partial C}{\partial z^{\prime\prime}}∂z′′∂C，它们分别乘以w3w_3w3和w4w_4w4，然后求和得到的结果再乘上σ′(z)\sigma^\prime(z)σ′(z)
就得到了∂C∂z\frac{\partial C}{\partial z}∂z∂C

zzz在正向传播的过程中已经知道了，因此这里的σ′(z)\sigma^\prime(z)σ′(z)是一个常数。

说了这么多，还是没说怎么计算∂C∂z′\frac{\partial C}{\partial z^\prime}∂z′∂C和∂C∂z′′\frac{\partial C}{\partial z^{\prime\prime}}∂z′′∂C啊。别急，下面就开始计算。

这里要分两种情况考虑：