斐波那契查找算法——深入理解，详细推导

斐波那契查找算法又称黄金分割查找算法。黄金分割点是把一条线段分成两个部分，使其中一部分与全长之比等于另一部分与这部分之比。取其前三位数字的近似值是0.618。

了解斐波那契查找算法就必须了解斐波那契数列，例如这样一组数列{1，1，2，3，5，8，13，21，34，55}。其中每项的值等于前两项之和，两个相邻数字的比列无线接近与0.618。

关于斐波那契算法，（以下截图来自韩顺平老师数据结构与算法的教学视频）链接

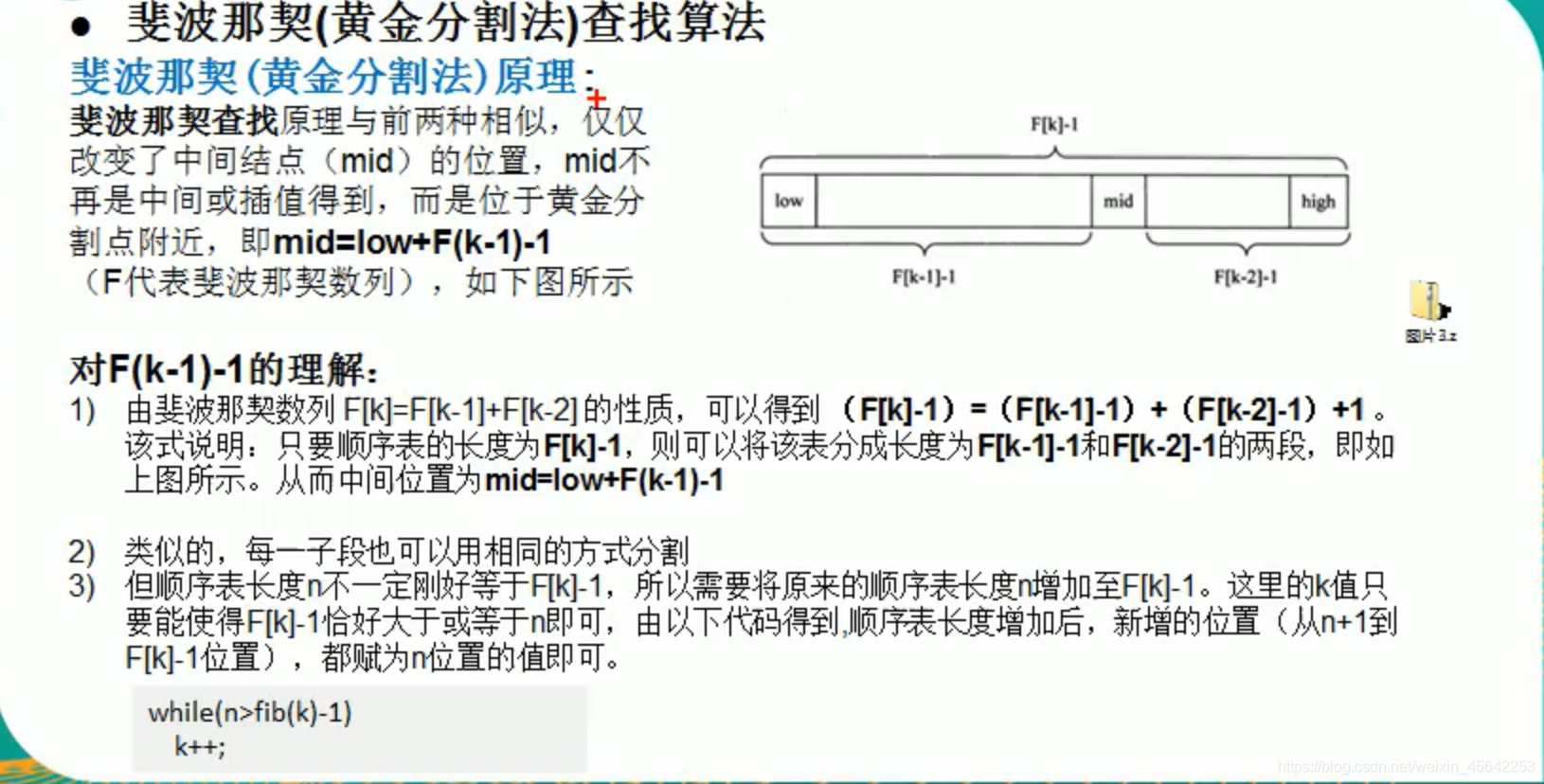
补充：理解mid = low + F(k - 1) - 1对于后面写程序至关重要，其中式子F[K] - 1 = (F[k - 1] - 1) + (F[k - 2] - 1) + 1；这里面‘1‘就代表mid。

（这段是重点：）
可以看到，斐波那契查找算法的思路就是把一个斐波那契数列映射到原需要查询的数列。通过将斐波那契数列中的每一项的值看成是一个数列中元素的个数，其中，斐波那契数列中的每一项减去1就代表原数列中的下标，因为原数列起始下标是从0开始的。关键是要理解斐波那契是如何对原数列进行划分的。它的划分规则就是借助于一个斐波那契数列。例如有一斐波那契数列{1，1，2，3，5，8，13}，假设长度13是我们需要查询的原数列。根据斐波那契的规则：每项等于前两项之和，比如这里的13 = 8 + 5。然后根据这个规则映射到对原数组划分，则长度13的原数组划分为长度8，和5两个部分。所以对应的下标就是一部分{0到7}（这部分就是F[k - 1],其中的k表示斐波那契数列的下标），另一部分{8到12}(这一部分就是F[k - 2],k同前)。所以根据公式mid = low + F(k - 1) - 1,算出mid = 0 + 8 - 1 等于7,所以原查询数列下标为7是中间值，这也验证了上述的划分结果没有错误，接下来如果没有找到就需要在第一轮划分上接着划分，过程是一样的，都需要借助斐波那契数列。到此，相信读者已经明白了整个过程。（笔者自认为这一段讲述是非常清晰、成功的哈哈哈）。

还有一点需要注意：由于斐波那契数列中的每一项我们看成是一个数列的元素个数，而斐波那契数列中的每一项的值是固定了的，但它却不包含所有的值。所以我们需要将原需要查询的数列扩容到大小离斐波那契数列中最接近的那一个数。例如斐波那契数列中有13这么一个项，而我此时的数列长度只有12，所以需要将原数列扩容到13。至于扩容的过程，在代码中体会吧。到此为止，是不是特别清晰明了了？

最后给出完整的代码，细节就在代码中慢慢体会吧：

/**
* 斐波那契查找算法非递归实现
*
* @param arr   待查询的数组
* @param value 查询的值
* @return 位置结果（下标）
*/

public static int fibonacciSearch(int[] arr, int value) {
int low = 0;//起始下标
int height = arr.length - 1;//最末尾的下标
int mid = 0;//初始化中间值
int[] f = fib();//获取斐波那契数列
int k = 0;//斐波那契数组下标
//这个循环的作用就是找到待查询数组大小在斐波那契数列中最接近的值
while (height > f[k] - 1) {
k++;
}
//数组扩容
int[] temp = Arrays.copyOf(arr, f[k]);
//默认扩容的后面结果都是0，这个循环的作用就是将扩容出来的地方都存储原数列最后一个数据
//例如：{1,3,4,35,66，0，0，0} ===》{1,3,4,35,66,66,66,66}
for (int i = height + 1; i < temp.length; i++) {
temp[i] = arr[height];
}
//开始循环查找，直到找到查找值的下标
while (low <= height) {
mid = low + f[k - 1] - 1;//mid求算算法
if (value < temp[mid]) {
height = mid - 1;
//说明：为什么k - 1
//当value < temp[mid]所以向左查找，而f[k - 1]代表左部分
k -= 1;
} else if (value > temp[mid]) {
low = mid + 1;
//说明：为什么k - 2
//当value > temp[mid]所以向右查找，而f[k - 2]代表右部分
//为什么又要k - 1呢？
// 这里经过测试这样才能防止数组下标越界。如果待查数列个数是奇数，如果一直 - 2，到最后k就为等于0
//再执行上面的f[k - 1]就会越界,由于斐波那契数列的第一项和第二项都是1所以当k = 2时直接- 1就好了
//这样也避免了下标越界
if (k == 2) {
k -= 1;
} else {
k -= 2;
}
} else {
//这里的if分支语句判断的是查找的元素是不是扩充部分，由于扩充部分的值就是原数列最后一位的值，
//而且扩充部分在原数列中是不存在的，所以直接用原数列最后一位的位置代替
if (mid <= height) {
return mid;
} else {
return height;
}
}
}
//没有找到
return -1;
}

小小总结一下吧：不管是斐波那契查找算法还是之前谈到的插值查询算法，思想都是跟二分查找思想类似，只是查询mid的算法不同，而斐波那契查找算法是需要通过斐波那契数列间接求算的。

以上代码过程，注释给的非常详细了。慢慢分析，相信读者一定会有所收获。