Lecture 17: Orthogonal Matrices and Gram-Schmidt

MIT 公开课：Gilbert Strang《线性代数》课程笔记（汇总

标准正交基

qiTqj={1(i=j)0(i≠j)q_i^Tq_j = \left\{\begin{array}{cc} 1 (i = j) \\ 0(i ≠ j) \\ \end{array}\right. qiT​qj​={1(i=j)0(i̸​=j)​

正交矩阵

定义

Q是正交矩阵，当它的各个列向量都相互正交的时候。

Q=[q1q2q3....]Q = [q_1 q_2 q_3 ....]Q=[q1​q2​q3​....] (qi是列向量q_i 是列向量qi​是列向量)

性质

如果Q是正交矩阵，那么

正交矩阵的投影矩阵

P是投影到正交矩阵Q的列空间所对应的投影矩阵。

• 据前几讲，

  P=Q(QTQ)−1QT=QQTP = Q(Q^TQ)^-1Q^T = QQ^TP=Q(QTQ)−1QT=QQT

  如果Q是方阵，那么 P=IP = IP=I

• 据前几讲， P 满足 P=PTP = P^TP=PT, P2=PP^2 = PP2=P 在这里同样成立

施密特正交化

过程

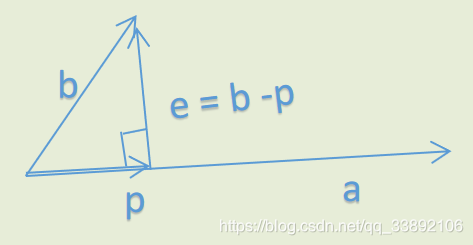
如上图，a和b是两个不相互正交的分量。

施密特正交化就是a不动，找到b中与a正交的分量。

• 方法：
  将b投影到a上，b - 投影分量 = e 就是所要求的。

• 据前几讲，e=b−(ATb/ATA)Ae = b - (A^Tb/A^TA)Ae=b−(ATb/ATA)A, 若要归一化再除以长度

一个例子：

A 经过施密特正交化变成Q，但是列空间并没有变