时间序列分析(一)
2018-02-26 13:38
169 查看
时间序列分析是根据系统观测得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法。它一般采用曲线拟合和参数估计方法(如非线性最小二乘法)进行。时间序列分析常用在国民经济宏观控制、区域综合发展规划、企业经营管理、市场潜量预测、气象预报、水文预报、地震前兆预报、农作物病虫灾害预报、环境污染控制、生态平衡、天文学和海洋学等方面。
在时间序列分析中,AR,MA,ARMA,ARIMA,ARCH,GARCH是最常见的模型,他们的区别主要在于适用条件不同,且是层层递进的,后面的一个模型解决了前一个模型的某个固有问题。时间序列分析也是一种回归,目的是用变量过去的观测值来预测同一变量的未来值。
AR (Auto Regressive)自回归模型: AR模型是一种线性预测,即已知N个数据,可由模型推出第N点前面或后面的数据(设推出P点). 本质类似于插值,其目的都是为了增加有效数据,只是AR模型是由N点递推,而插值是由两点(或少数几点)去推导多点,所以AR模型要比插值方法效果更好。
MA(Moveing Average)移动平模型:分两种形式:
简单移动平均法: 设有一时间序列y1,y2,..., 则按数据点的顺序逐点推移求出N个数的平均数,即可得到一次移动平均数.
趋势移动平均法 :当时间序列没有明显的趋势变动时,使用一次移动平均就能够准确地反映实际情况,直接用第t周期的一次移动平均数就可预测第1t+周期之值。时间序列出现线性变动趋势时,用一次移动平均数来预测就会出现滞后偏差。修正的方法是在一次移动平均的基础上再做二次移动平均,利用移动平均滞后偏差的规律找出曲线的发展方向和发展趋势,然后才建立直线趋势的预测模型。故称为趋势移动平均法。
ARMA(Auto Regressive And Moveing Average)自回归滑动平均模型:其建模思想可概括为:逐渐增加模型的阶数,拟合较高阶模型,直到再增加模型的阶数而剩余残差方差不再显著减小为止。
ARIMA(Auto Regressive Integrated Moveing Average)差分自回归滑动平均模型: 一般关注的有趋势和季节/循环成分的时间序列都是不平稳的,这就需要对时间序列进行差分来消除这些使序列不平稳的成分,而使其变成平稳的时间序列,并估计ARMA模型,估计之后再转变该模型,使之适应于差分之前的序列,得到的模型称为ARIMA模型。
ARCH(Autoregressive conditional heteroskedasticity model)自回归条件异方差模型:解决了传统的计量经济学对时间序列变量的第二个假设(方差恒定)所引起的问题
GARCH(Generalized AutoRegressive Conditional Heteroskedasticity)广义ARCH模型:GARCH模型是一个专门针对金融数据所量体订做的回归模型,除去和普通回归模型相同的之处,GARCH对误差的方差进行了进一步的建模。特别适用于波动性的分析和预测,这样的分析对投资者的决策能起到非常重要的指导性作用,其意义很多时候超过了对数值本身的分析和预测。
时间序列建模基本步骤:
第一步 收集历史资料,加以整理,编成时间序列,并根据时间序列绘成统计图。时间序列分析通常是把各种可能发生作用的因素进行分类,传统的分类方法是按各种因素的特点或影响效果分为四大类:(1)长期趋势;(2)季节变动;(3)循环变动;(4)不规则变动。
第二步 分析时间序列。时间序列中的每一时期的数值都是由许许多多不同的因素同时发生作用后的综合结果。
第三步 求时间序列的长期趋势(T)季节变动(s)和不规则变动(I)的值,并选定近似的数学模式来代表它们。对于数学模式中的诸未知参数,使用合适的技术方法求出其值。
第四步 利用时间序列资料求出长期趋势、季节变动和不规则变动的数学模型后,就可以利用它来预测未来的长期趋势值T和季节变动值s,在可能的情况下预测不规则变动值I。然后用以下模式计算出未来的时间序列的预测值Y:
加法模式T+S+I=Y
乘法模式T×S×I=Y
如果不规则变动的预测值难以求得,就只求长期趋势和季节变动的预测值,以两者相乘之积或相加之和为时间序列的预测值。如果经济现象本身没有季节变动或不需预测分季分月的资料,则长期趋势的预测值就是时间序列的预测值,即T=Y。但要注意这个预测值只反映现象未来的发展趋势,即使很准确的趋势线在按时间顺序的观察方面所起的作用,本质上也只是一个平均数的作用,实际值将围绕着它上下波动。
辨识合适的随机模型,进行曲线拟合,即用通用随机模型去拟合时间序列的观测数据。对于短的或简单的时间序列,可用趋势模型和季节模型加上误差来进行拟合。对于平稳时间序列,可用通用ARMA模型(自回归滑动平均模型)及其特殊情况的自回归模型、滑动平均模型或组合-ARMA模型等来进行拟合。当观测值多于50个时一般都采用ARMA模型。对于非平稳时间序列则要先将观测到的时间序列进行差分运算,化为平稳时间序列,再用适当模型去拟合这个差分序列。
时间序列的预处理
时间序列的预处理是对一个观察值序列的纯随机性和平稳性进行检验,根据检验结果可以将此序列分为不同的类型,纯随机序列也称为白噪声序列,是没有任何信息可以提取的平稳随机序列。
通过预处理将序列分成不同类型之后我们就可以根据各种序列类型的特点使用不同的模型建模,常见的平稳时间序列建模模型为ARMA(可以分为AR、MA和ARMA三类),此模型是使用线性模型来拟合平稳序列。非平稳的序列分析可以建立的模型有ARIMA以及残差自回归模型等等。
平稳时间序列
2.1 基本概念
ARMA模型,如下结构可以简记为ARMA(p,q): 该模型要求时间序列满足平稳性(stationarity)和可逆性(invertibility)的条件。
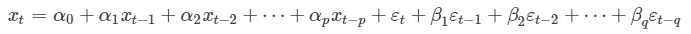
当q=0时,是AR(p)模型:
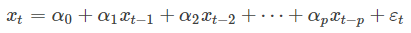
当p=0时,是MA(q)模型:
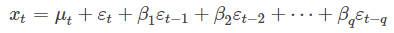
自相关系数(ACF):平稳模型的自相关系数如下,其中σt为观测序列在时间t的标准差。 【自相关函数描述观测值和前面的预测值的相关系数】
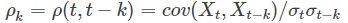
偏自相关系数(PACF): 对于一个平稳AR(p)模型,求出滞后k自相关系数ρk时,实际上得到并不是Xt与Xt−k之间单纯的相关关系。因为Xt同时还会受到中间k-1个随机变量Xt−1、Xt−2、……、Xt−k+1的影响。 为了能单纯度量Xt−k对Xt的影响,引进偏自相关系数(PACF)的概念: 对于平稳时间序列{Xt},在剔除了中间k-1个随机变量量Xt−1、Xt−2、……、Xt−k+1的干扰之后,Xt−k对Xt影响的相关程度。【在给定中间观测值的条件下观测值和前面某间隔的预测值的相关系数】
拖尾和截尾: 拖尾是系数随着k的增大衰减,但始终有非零取值,截尾是k增大到一定大小时系数取零值。
2.2 平稳时间序列建模
对一个时间序列经过预处理,若被判定为平稳非白噪声序列,则可以计算ACF和PACF,根据上述两个系数选取合适的模型,并且为模型定阶。

拖尾、截尾示意说明,如下图:

左边的 acf 条形图是衰减的指数型波动;这种图形称为拖尾。而右边的pacf条形图是第二个条(p=2)之后就很小,而且没有什么模式;这种图形称为在p=2后截尾。这说明该数据满足是平稳的AR(2)模型。
非平稳时间序列
非平稳时间序列可以建立的模型有ARIMA以及残差自回归模型等等,这里主要讨论ARIMA。
差分运算:相距k期的两个序列之间的减法称为k阶差分运算。
对于非平稳时间序列,我们可以通过相应的变换将其变为平稳序列。差分是一个主要的手段,一个线性趋势的非平稳序列可以使用d阶差分运算,化为平稳时间序列,而一个指数趋势的非平稳序列可以先取对数再差分化为平稳序列。画出原始数据的时序图从时序图可以看出数据的基本趋势:围绕某水平线波动;围绕某直线波动;呈指数上升或下降趋势等等。当然如果变换后的序列依然非平稳,既可以考虑修改一下变换方法,也可以考虑再作一次差分。
ARIMA模型实质上就是差分运算和ARMA模型的组合,非平稳序列经过变换后变成了平稳序列,此时我们就可以使用ARMA模型对时间序列建模了。
平稳性的检验
在应用过程中,时间序列的平稳性的判断要简单的多。常用的判断时间序列平稳性的方法有两个:图示法和单位根检验法。
图示法,顾名思义,就是画出时间序列的时序图,来目测时间序列是否平稳。如果画出的时间序列不存在明显的趋势,那么时间序列可能是平稳的。这个方法比较随意和主观,因此,只能作为辅助判断的手段。
单位根检验法是一个理论基础扎实的判断手段,单位根检验的方法非常多,一般常用的有DF检验(Dickey-Fuller Test),ADF检验(Augmented Dickey-Fuller Test)和PP检验(Phillips-Perron Test)。
单位根检验
单位根检验是指检验序列中是否存在单位根,因为存在单位根就是非平稳时间序列了。单位根就是指单位根过程,可以证明,序列中存在单位根过程就不平稳,会使回归分析中存在伪回归。有6种单位根检验方法:ADF检验、DFGLS检验、PP检验、KPSS检验、ERS检验和NP检验。
迪基-福勒检验(DF): 在统计学里,迪基-福勒检验(Dickey-Fuller test)可以测试一个自回归模型是否存在单位根(unit root)。迪基-福勒检验模式是D. A迪基和W. A福勒建立的。DF检验只有当序列为AR(1)时才有效。如果序列存在高阶滞后相关,这就违背了扰动项是独立同分布的假设。在这种情况下,可以使用ADF检验方法(augmented Dickey-Fuller test )来检验含有高阶序列相关的序列的单位根。
tseries::adf.test(x)
ADF(Augmented Dickey--Fuller test for unit roots)增广的DF检验,原假设含单位根(非平稳)
```{r}
library(fUnitRoots)
urdfTest(x)
```
1%:严格拒绝原假设;5%:拒绝原假设,10%类推。这三个水平值是软件设定的,它表示拒绝原假设的不同程度。
ADF检验的原假设是存在单位根,输出的是ADF检验的统计值,只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设,认为数据平稳。注意,ADF值一般是负的,也有正的,但是它只有小于1%水平下的才能认为是及其显著的拒绝原假设 。
一般在原序列条件下,如果存在非平稳状态,按以下步骤进行:
一阶差分是否具有单位根,就是比较一阶差分的ADF检验值与5%临界值的大小,否则再看二阶差分。
差分变换
对于这样非平稳的时间序列,能否使用ARIMA模型进行拟合呢?答案自然是可以的,我们只需要通过差分变换,就可以将非平稳序列转换为平稳序列。
具体来讲的话,差分就是将时间序列中的每一个观测值Yt都替换为Yt - Y{t-1},一次差分可以消除时间序列中的线性趋势,二次差分可以消除时序中的二次趋势,三次差分可以消除时序中的三次项趋势,以此类推。但需要注意的是,对时间序列进行两次以上的差分通常都是不必要的,毕竟我们无法对差分后的数据进行合理的解释。
使用R中自带的diff()函数与forecast包中的ndiffs()函数均可以进行差分,diff函数会返回差分后的数据,ndiffs函数可以帮助我们最优的d值。
参考资料:
http://blog.csdn.net/MacanS/article/details/52842839
在时间序列分析中,AR,MA,ARMA,ARIMA,ARCH,GARCH是最常见的模型,他们的区别主要在于适用条件不同,且是层层递进的,后面的一个模型解决了前一个模型的某个固有问题。时间序列分析也是一种回归,目的是用变量过去的观测值来预测同一变量的未来值。
AR (Auto Regressive)自回归模型: AR模型是一种线性预测,即已知N个数据,可由模型推出第N点前面或后面的数据(设推出P点). 本质类似于插值,其目的都是为了增加有效数据,只是AR模型是由N点递推,而插值是由两点(或少数几点)去推导多点,所以AR模型要比插值方法效果更好。
MA(Moveing Average)移动平模型:分两种形式:
简单移动平均法: 设有一时间序列y1,y2,..., 则按数据点的顺序逐点推移求出N个数的平均数,即可得到一次移动平均数.
趋势移动平均法 :当时间序列没有明显的趋势变动时,使用一次移动平均就能够准确地反映实际情况,直接用第t周期的一次移动平均数就可预测第1t+周期之值。时间序列出现线性变动趋势时,用一次移动平均数来预测就会出现滞后偏差。修正的方法是在一次移动平均的基础上再做二次移动平均,利用移动平均滞后偏差的规律找出曲线的发展方向和发展趋势,然后才建立直线趋势的预测模型。故称为趋势移动平均法。
ARMA(Auto Regressive And Moveing Average)自回归滑动平均模型:其建模思想可概括为:逐渐增加模型的阶数,拟合较高阶模型,直到再增加模型的阶数而剩余残差方差不再显著减小为止。
ARIMA(Auto Regressive Integrated Moveing Average)差分自回归滑动平均模型: 一般关注的有趋势和季节/循环成分的时间序列都是不平稳的,这就需要对时间序列进行差分来消除这些使序列不平稳的成分,而使其变成平稳的时间序列,并估计ARMA模型,估计之后再转变该模型,使之适应于差分之前的序列,得到的模型称为ARIMA模型。
ARCH(Autoregressive conditional heteroskedasticity model)自回归条件异方差模型:解决了传统的计量经济学对时间序列变量的第二个假设(方差恒定)所引起的问题
GARCH(Generalized AutoRegressive Conditional Heteroskedasticity)广义ARCH模型:GARCH模型是一个专门针对金融数据所量体订做的回归模型,除去和普通回归模型相同的之处,GARCH对误差的方差进行了进一步的建模。特别适用于波动性的分析和预测,这样的分析对投资者的决策能起到非常重要的指导性作用,其意义很多时候超过了对数值本身的分析和预测。
时间序列建模基本步骤:
第一步 收集历史资料,加以整理,编成时间序列,并根据时间序列绘成统计图。时间序列分析通常是把各种可能发生作用的因素进行分类,传统的分类方法是按各种因素的特点或影响效果分为四大类:(1)长期趋势;(2)季节变动;(3)循环变动;(4)不规则变动。
第二步 分析时间序列。时间序列中的每一时期的数值都是由许许多多不同的因素同时发生作用后的综合结果。
第三步 求时间序列的长期趋势(T)季节变动(s)和不规则变动(I)的值,并选定近似的数学模式来代表它们。对于数学模式中的诸未知参数,使用合适的技术方法求出其值。
第四步 利用时间序列资料求出长期趋势、季节变动和不规则变动的数学模型后,就可以利用它来预测未来的长期趋势值T和季节变动值s,在可能的情况下预测不规则变动值I。然后用以下模式计算出未来的时间序列的预测值Y:
加法模式T+S+I=Y
乘法模式T×S×I=Y
如果不规则变动的预测值难以求得,就只求长期趋势和季节变动的预测值,以两者相乘之积或相加之和为时间序列的预测值。如果经济现象本身没有季节变动或不需预测分季分月的资料,则长期趋势的预测值就是时间序列的预测值,即T=Y。但要注意这个预测值只反映现象未来的发展趋势,即使很准确的趋势线在按时间顺序的观察方面所起的作用,本质上也只是一个平均数的作用,实际值将围绕着它上下波动。
辨识合适的随机模型,进行曲线拟合,即用通用随机模型去拟合时间序列的观测数据。对于短的或简单的时间序列,可用趋势模型和季节模型加上误差来进行拟合。对于平稳时间序列,可用通用ARMA模型(自回归滑动平均模型)及其特殊情况的自回归模型、滑动平均模型或组合-ARMA模型等来进行拟合。当观测值多于50个时一般都采用ARMA模型。对于非平稳时间序列则要先将观测到的时间序列进行差分运算,化为平稳时间序列,再用适当模型去拟合这个差分序列。
时间序列的预处理
时间序列的预处理是对一个观察值序列的纯随机性和平稳性进行检验,根据检验结果可以将此序列分为不同的类型,纯随机序列也称为白噪声序列,是没有任何信息可以提取的平稳随机序列。
通过预处理将序列分成不同类型之后我们就可以根据各种序列类型的特点使用不同的模型建模,常见的平稳时间序列建模模型为ARMA(可以分为AR、MA和ARMA三类),此模型是使用线性模型来拟合平稳序列。非平稳的序列分析可以建立的模型有ARIMA以及残差自回归模型等等。
平稳时间序列
2.1 基本概念
ARMA模型,如下结构可以简记为ARMA(p,q): 该模型要求时间序列满足平稳性(stationarity)和可逆性(invertibility)的条件。
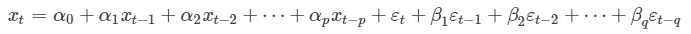
当q=0时,是AR(p)模型:
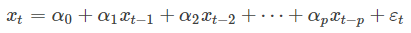
当p=0时,是MA(q)模型:
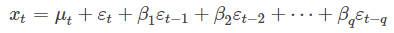
自相关系数(ACF):平稳模型的自相关系数如下,其中σt为观测序列在时间t的标准差。 【自相关函数描述观测值和前面的预测值的相关系数】
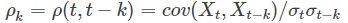
偏自相关系数(PACF): 对于一个平稳AR(p)模型,求出滞后k自相关系数ρk时,实际上得到并不是Xt与Xt−k之间单纯的相关关系。因为Xt同时还会受到中间k-1个随机变量Xt−1、Xt−2、……、Xt−k+1的影响。 为了能单纯度量Xt−k对Xt的影响,引进偏自相关系数(PACF)的概念: 对于平稳时间序列{Xt},在剔除了中间k-1个随机变量量Xt−1、Xt−2、……、Xt−k+1的干扰之后,Xt−k对Xt影响的相关程度。【在给定中间观测值的条件下观测值和前面某间隔的预测值的相关系数】
拖尾和截尾: 拖尾是系数随着k的增大衰减,但始终有非零取值,截尾是k增大到一定大小时系数取零值。
2.2 平稳时间序列建模
对一个时间序列经过预处理,若被判定为平稳非白噪声序列,则可以计算ACF和PACF,根据上述两个系数选取合适的模型,并且为模型定阶。

拖尾、截尾示意说明,如下图:

左边的 acf 条形图是衰减的指数型波动;这种图形称为拖尾。而右边的pacf条形图是第二个条(p=2)之后就很小,而且没有什么模式;这种图形称为在p=2后截尾。这说明该数据满足是平稳的AR(2)模型。
非平稳时间序列
非平稳时间序列可以建立的模型有ARIMA以及残差自回归模型等等,这里主要讨论ARIMA。
差分运算:相距k期的两个序列之间的减法称为k阶差分运算。
对于非平稳时间序列,我们可以通过相应的变换将其变为平稳序列。差分是一个主要的手段,一个线性趋势的非平稳序列可以使用d阶差分运算,化为平稳时间序列,而一个指数趋势的非平稳序列可以先取对数再差分化为平稳序列。画出原始数据的时序图从时序图可以看出数据的基本趋势:围绕某水平线波动;围绕某直线波动;呈指数上升或下降趋势等等。当然如果变换后的序列依然非平稳,既可以考虑修改一下变换方法,也可以考虑再作一次差分。
ARIMA模型实质上就是差分运算和ARMA模型的组合,非平稳序列经过变换后变成了平稳序列,此时我们就可以使用ARMA模型对时间序列建模了。
平稳性的检验
在应用过程中,时间序列的平稳性的判断要简单的多。常用的判断时间序列平稳性的方法有两个:图示法和单位根检验法。
图示法,顾名思义,就是画出时间序列的时序图,来目测时间序列是否平稳。如果画出的时间序列不存在明显的趋势,那么时间序列可能是平稳的。这个方法比较随意和主观,因此,只能作为辅助判断的手段。
单位根检验法是一个理论基础扎实的判断手段,单位根检验的方法非常多,一般常用的有DF检验(Dickey-Fuller Test),ADF检验(Augmented Dickey-Fuller Test)和PP检验(Phillips-Perron Test)。
单位根检验
单位根检验是指检验序列中是否存在单位根,因为存在单位根就是非平稳时间序列了。单位根就是指单位根过程,可以证明,序列中存在单位根过程就不平稳,会使回归分析中存在伪回归。有6种单位根检验方法:ADF检验、DFGLS检验、PP检验、KPSS检验、ERS检验和NP检验。
迪基-福勒检验(DF): 在统计学里,迪基-福勒检验(Dickey-Fuller test)可以测试一个自回归模型是否存在单位根(unit root)。迪基-福勒检验模式是D. A迪基和W. A福勒建立的。DF检验只有当序列为AR(1)时才有效。如果序列存在高阶滞后相关,这就违背了扰动项是独立同分布的假设。在这种情况下,可以使用ADF检验方法(augmented Dickey-Fuller test )来检验含有高阶序列相关的序列的单位根。
tseries::adf.test(x)
ADF(Augmented Dickey--Fuller test for unit roots)增广的DF检验,原假设含单位根(非平稳)
```{r}
library(fUnitRoots)
urdfTest(x)
```
1%:严格拒绝原假设;5%:拒绝原假设,10%类推。这三个水平值是软件设定的,它表示拒绝原假设的不同程度。
ADF检验的原假设是存在单位根,输出的是ADF检验的统计值,只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设,认为数据平稳。注意,ADF值一般是负的,也有正的,但是它只有小于1%水平下的才能认为是及其显著的拒绝原假设 。
一般在原序列条件下,如果存在非平稳状态,按以下步骤进行:
一阶差分是否具有单位根,就是比较一阶差分的ADF检验值与5%临界值的大小,否则再看二阶差分。
差分变换
对于这样非平稳的时间序列,能否使用ARIMA模型进行拟合呢?答案自然是可以的,我们只需要通过差分变换,就可以将非平稳序列转换为平稳序列。
具体来讲的话,差分就是将时间序列中的每一个观测值Yt都替换为Yt - Y{t-1},一次差分可以消除时间序列中的线性趋势,二次差分可以消除时序中的二次趋势,三次差分可以消除时序中的三次项趋势,以此类推。但需要注意的是,对时间序列进行两次以上的差分通常都是不必要的,毕竟我们无法对差分后的数据进行合理的解释。
使用R中自带的diff()函数与forecast包中的ndiffs()函数均可以进行差分,diff函数会返回差分后的数据,ndiffs函数可以帮助我们最优的d值。
参考资料:
http://blog.csdn.net/MacanS/article/details/52842839
相关文章推荐
- python 金融应用(四)金融时间序列分析基础
- 金融时间序列分析:6. AR模型实例(R语言)
- R语言2——时间序列分析
- 时间序列分析及应用 R语言 读书笔记 03
- 金融时间序列分析:1. 基础知识
- 应用时间序列分析(王燕)学习笔记3
- Python_Statsmodels包_时间序列分析_ARIMA模型
- 时间序列分析
- R(2)时间序列分析及应用之TSA安装(R语言)
- 时间序列分析之一次指数平滑法
- 非平稳时间序列趋势分析
- R中季节性时间序列分析及非季节性时间序列分析
- [python] 时间序列分析之ARIMA
- pandas时间序列分析和处理Timeseries
- pandas小记:pandas时间序列分析和处理Timeseries
- Excel在统计分析中的应用—第十三章—时间序列分析-季节变动的测定(季节虚拟变量回归法)
- 时间序列分析中的ARMA,ARIMA模型整体综述
- 多元时间序列分析基础二
- 时间序列的认识及增长分析
- 应用时间序列分析(王燕)学习笔记1
