时间复杂度和空间复杂度
2017-08-17 10:38
288 查看
将算法中基本操作的执行次数作为算法的时间复杂度
T(n)=O(f(n)中增长最快的项/ 此项的系数) , 比如f(n)=2n3+4n2+100 , 则其时间复杂度为为T(n)=O(2n3/2)=O(n3)。
常用的比较关系如下:
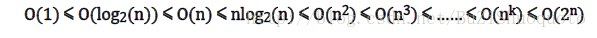
通过以上分析我们总结出计算一个算法时间复杂度的步骤如下:
(1) 确定算法中的基本操作,以及问题的规模。
(2)根据基本操作执行情况计算出规模n 的函数f(n),并确定时间复杂度为T(n)=O(f(n)中增长最快的项/此项的系数)。
注意:有的算法中基本操作执行次数跟初始输入的数据有关。如果题目不做特殊要求,
一般我们依照使得基本操作执行次数最多的输入来计算时间复杂度,即将最坏的情况作为
算法时间复杂度的度量。
1.2.2 例题选讲
例题1:求出以下算法的时间复杂度。
分析:
第一步:找出基本操作,确定规模n。
找基本操作(所谓基本操作,即其重复执行次数和算法的执行时间成正比的操作,通俗点说,这种操作组成了算法,当它们都执行完的时候算法也结束了,多数情况下我们取最深层循环内的语句所描述的操作作为基本操作),显然题目中j++;与i+=2;这两行都可以
第二步:计算出n 的函数f(n)。
显然,n 确定以后,循环的结束与否与i 有关,i 的初值为1,每次自增2,假设i 自增m 次后循环结束,则i 最后的值为1+2×m,因此有1+2×m+K=n(其中K 为一个常数,
因为在循环结束时i 的值稍大于n,为了方便表述和进一步计算,用K 将1+2×m 修正成n。
因为K 为常数,所以这样做不会影响最终时间复杂度的计算),解得m=(n-1-K)/2,即
f(n)=(n-1-K)/2,可以发现其中增长最快的项为n/2,因此时间复杂度T(n)=O(n)。
例题2:分析以下算法的时间复杂度。
分析:
x++;处于最内层循环,因此取x++;做为基本操作。显然n 为规模。可以算出x++;的
执行次数为f(n)=n(n-1)/2,变化最快的项为n2,因此时间复杂度为T(n)=O(n2)。
例题3:分析以下算法的时间复杂度。
分析:
显然n 为规模,基本操作为i++;s=s+i;i 与s 都从0 开始,假设循环执行m 次结束,
则有s1=1,s2=1+2=3,s3=1+2+3=6, ……,sm=m(m+1)/2(其中sm 为执行到第m 次的时
候s 的值),则有m(m+1)/2+K=n,(K 为起修正作用的常数)由求根公式得:
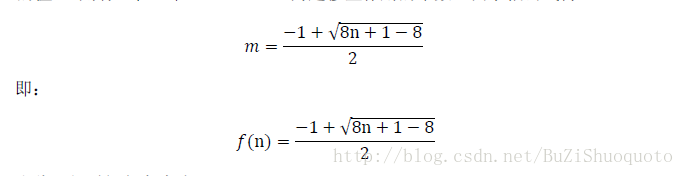
即:
由此可知时间复杂度为:
T(n)=O(√n)
T(n)=O(f(n)中增长最快的项/ 此项的系数) , 比如f(n)=2n3+4n2+100 , 则其时间复杂度为为T(n)=O(2n3/2)=O(n3)。
常用的比较关系如下:
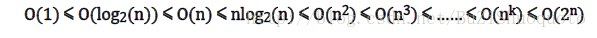
通过以上分析我们总结出计算一个算法时间复杂度的步骤如下:
(1) 确定算法中的基本操作,以及问题的规模。
(2)根据基本操作执行情况计算出规模n 的函数f(n),并确定时间复杂度为T(n)=O(f(n)中增长最快的项/此项的系数)。
注意:有的算法中基本操作执行次数跟初始输入的数据有关。如果题目不做特殊要求,
一般我们依照使得基本操作执行次数最多的输入来计算时间复杂度,即将最坏的情况作为
算法时间复杂度的度量。
1.2.2 例题选讲
例题1:求出以下算法的时间复杂度。
void fun(int n)
{
int i=1,j=100;
while(i<n)
{
j++;
i+=2;
}
}分析:
第一步:找出基本操作,确定规模n。
找基本操作(所谓基本操作,即其重复执行次数和算法的执行时间成正比的操作,通俗点说,这种操作组成了算法,当它们都执行完的时候算法也结束了,多数情况下我们取最深层循环内的语句所描述的操作作为基本操作),显然题目中j++;与i+=2;这两行都可以
第二步:计算出n 的函数f(n)。
显然,n 确定以后,循环的结束与否与i 有关,i 的初值为1,每次自增2,假设i 自增m 次后循环结束,则i 最后的值为1+2×m,因此有1+2×m+K=n(其中K 为一个常数,
因为在循环结束时i 的值稍大于n,为了方便表述和进一步计算,用K 将1+2×m 修正成n。
因为K 为常数,所以这样做不会影响最终时间复杂度的计算),解得m=(n-1-K)/2,即
f(n)=(n-1-K)/2,可以发现其中增长最快的项为n/2,因此时间复杂度T(n)=O(n)。
例题2:分析以下算法的时间复杂度。
void fun(int n)
{
int i,j,x=0;
for(i=1;i<n;i++)
for(j=i+1;j<=n;j++)
x++;
}分析:
x++;处于最内层循环,因此取x++;做为基本操作。显然n 为规模。可以算出x++;的
执行次数为f(n)=n(n-1)/2,变化最快的项为n2,因此时间复杂度为T(n)=O(n2)。
例题3:分析以下算法的时间复杂度。
void fun(int n)
{
int i=0;s=0;
while(s<n)
{
i++;
s=s+i;
}
}分析:
显然n 为规模,基本操作为i++;s=s+i;i 与s 都从0 开始,假设循环执行m 次结束,
则有s1=1,s2=1+2=3,s3=1+2+3=6, ……,sm=m(m+1)/2(其中sm 为执行到第m 次的时
候s 的值),则有m(m+1)/2+K=n,(K 为起修正作用的常数)由求根公式得:
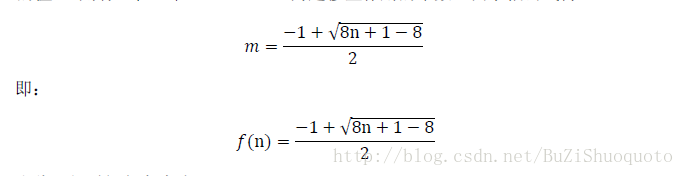
即:
由此可知时间复杂度为:
T(n)=O(√n)
相关文章推荐
- 数据结构--算法(时间复杂度和空间复杂度)
- 时间复杂度和空间复杂度详解
- 时间复杂度和空间复杂度1 – 数据结构和算法03
- 现有1,2……一直到n的无序数组,求排序算法,并且要求时间复杂度为O(n),空间复杂度为O(1),使用交换,而且只能交换两个数
- 时间复杂度和空间复杂度详解
- 时间复杂度和空间复杂度详解
- 学习笔记3 时间复杂度和空间复杂度
- 时间复杂度为O(n),空间复杂度为O(1)
- 时间复杂度和空间复杂度的分析
- N个大小不等的自然数排序,时间复杂度为O(n),空间复杂度为O(1)
- 大 Θ记号、大 Ω记号、空间复杂度、时间复杂度
- 时间复杂度和空间复杂度[数据结构]
- 给定一个存放整数的数组,重新排列数组使得数组左边为奇数,右边为偶数。要求:空间复杂度O(1),时间复杂度为O(n)
- (学习笔记 2)时间复杂度和空间复杂度
- 时间复杂度和空间复杂度2 – 数据结构和算法04
- 时间复杂度和空间复杂度的概念
- 时间复杂度和空间复杂度详解
- 数据结构和算法-时间复杂度和空间复杂度
- 时间复杂度和空间复杂度
- {转载}——时间复杂度和空间复杂度详解
