算法 排序算法之交换排序--冒泡排序和快速排序

交换排序

利用交换数据元素的位置进行排序的方法称为交换排序

常用的交换排序方法有

冒泡排序

快速排序

其中快速排序是一种分区交换方法[分治]

冒泡排序[相邻交换 一次交换只能消除一个逆序]

基本思想

设数组a中存放了n个数据元素，循环进行n-1次排序

第一次，依次比较相邻两个元素a[i]和a[i+1]，若为逆序，则交换两个元素，这样进行n-1次排序后数值最大的数据放在数组的末尾

第二次时，数据元素个数减1，操作方法与第一次类似，进行n-2次比较

排序过程

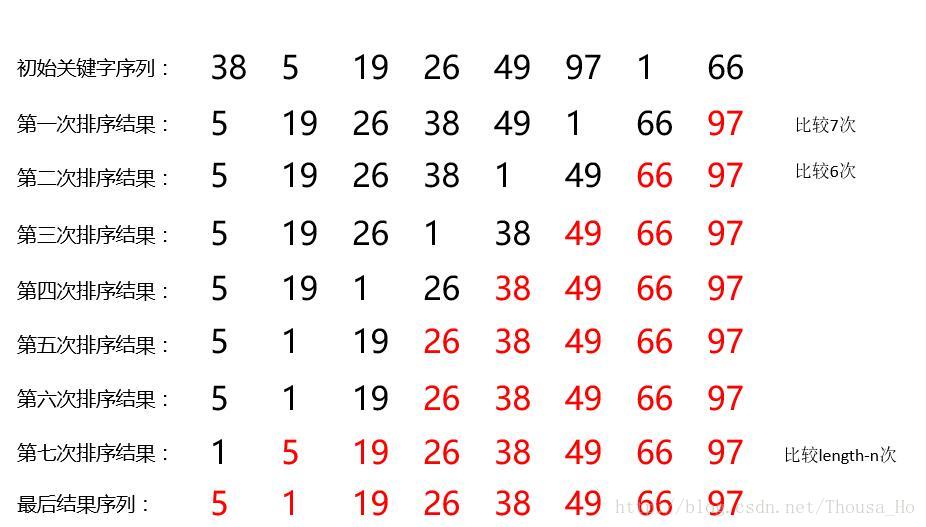
代码实现

有些待排序元素已经基本有 因此可以设置一个flag变量用于标记本次排序过程是否有交换动作，若没有则说明已经排好序，就可提前结束排序过程

Java代码

/**
* 冒泡排序
*/
public static void bubbleSort(int[] arr) {
int temp;
/*设置一个flag变量用于标记本次排序过程是否有交换动作，若没有则说明已经排好序，就可提前结束排序过程*/
boolean flag = false;
for (int i = 1; i < arr.length && !flag; i++) {
flag = true;
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
flag = false;
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}

C代码实现

void BubbleSort(Datatype a[],int n){
int i,j,flag=1;
DataType temp;

for (i=1;i<n&&flag==1;i++){
flag = 0;
for (j=0;j<n-1;j++){
if (a[j+1]<a[j]){
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
flag = 1;
}
}
}
}

算法分析

最好情况时间复杂度：

集合全部有序，每次都因无交换而退出，此时循环n-1次，时间复杂度为O(n);

最坏情况：

集合全部逆序存放，第一次比较n-1次，第二次比较n-2…最后比较1次，总的比较次数按照求和运算是n*(n-1)/2

移动次数是3n*(n-1)/2

平均时间复杂度

时间复杂度是O(n^2);

空间复杂度

没有使用额外的空间 因此空间复杂度是O(1)

稳定性

显然冒泡排序是一种稳定的排序算法

快速排序[不相邻交换 一次交换可能消除多个逆序]

快速排序是一种二叉树结构的交换排序方法

基本思想

设数组a中存放了n个数据元素，low为低端下标，high为高端下标

从数组中任取一个元素作为标准（一般取a[low]） 调整各个元素的位置，使排在标准元素之前的元素小于标准元素，排在后面的大于标准元素

一趟排序后，标准元素位置确定，且数组分为两个子数组，再分别最两个子数组进行方法类同的递归排序

递归的出口是high>low

排序过程

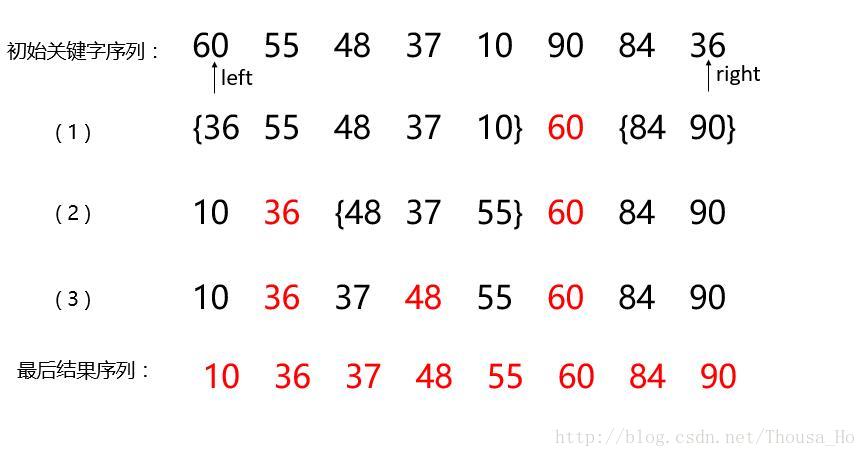
算法实现

C代码

void QuickSort(DataType a[],int low,int high){
int i=low,j=high;
DataType temp = a[low];

while (i<j){
while (i<j&&temp<=a[j]){//在数组右端扫描
j--;
}
if (i<j){
a[i++]=a[j];
}

while (i<j&&a[i]<temp){//在数组左端扫描
i++;
}
if (i<j){
a[j--]=a[i];
}
}
a[i] = temp;
if (low<i){//对左端子集合进行递归
QuickSort(a,low,i-1);
}
if (i<high){//对右端子集合进行递归
QuickSort(a,i+1,high);
}
}

Java代码实现

public static void quickSort(int[] arr, int head, int tail) {
if (head < tail) {
int left = head, right = tail;
int key = arr[head];
while (left < right) {
/*从右往左找出比key小的数*/
while (left < right && arr[right] >= key) {
right--;
}
if (left < right) {
/*找到的数放在left位置*/
arr[left++] = arr[right];
}

/*此时从左往右遍历出比key大的数*/
while (left < right && arr[left] < key) {
left++;
}
if (left < right) {
/*找到的数放在right位置*/
arr[right--] = arr[left];
}
}
arr[left] = key;
//递归遍历
quickSort(arr, head, left - 1);
quickSort(arr, left + 1, tail);
}
}

算法分析

最好情况时间复杂度

每次选取的标注元素都可以均分成两个子数组，此时是一个完全二叉树结构，每次比较的次数都接近n-1 因此时间复杂度是O（nlog2n）

最坏情况时间复杂度

当数组全部有序时，每次都分解成二叉退化树[单分支二叉树]，时间复杂度O(n^2)

平均时间复杂度

平均时间复杂度O（nlog2n）

空间复杂度

需要堆栈空间临时保存递归调用函数 堆栈空间的使用个数和递归调用的次数有关。最好情况是O（nlog2n），最坏情况是O(n)，平均空间复杂度O（log2n）

稳定性

快速排序是不稳定的排序算法