面试题50 树中两个节点的最低公共祖先LCA(Lowest Common Ancestor )
2015-05-20 09:58
267 查看
题目是树的最低公共祖先,我们先来考虑树是什么树?
我们从最简单的情况开始分析。
情况一:是二叉树,且是二叉搜索树(二叉排序树,二叉查找树)
分析:由于二叉排序树具有这样的特点:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉排序树。
所以我们只需要从树的根节点开始和输入的两个节点进行比较。如果当前节点的值比两个节点都大,那么最低公共父节点一定在当前节点的左子树中,于是下一步遍历当前节点的左子节点。如果当前节点比两个节点都大,那么最低公共父节点一定在当前节点的右子树中,于是下一步遍历当前节点的右子节点。这样从树中从上到下找到的第一个在输入节点的值之间的节点就是最低公共祖先。
struct
node //二叉树节点数据结构
{
int data;
struct node*
left;
struct node*
right;
};
struct node*
newNode(int );
Node*
findLowerstCommonAncestor(Node* root,int
value1,int value2)
{
while ( root!=
NULL )
{
int value=
root->getValue(); //获取当前节点的值
if ( value>
value1&& value>
value2 ) //当前节点的值大于两输入值
root = root->getLeft();
elseif
(value< value1&&
value< value2) //当前节点的值校园两输入值
root = root->getRight();
else
return root;
}
return NULL;
}
情况二:是二叉树,但是普通的二叉树


方法一:一个简单的复杂度为
O(n) 的算法,解决LCA问题
1) 找到从根到n1的路径,并存储在一个向量或数组中。
2)找到从根到n2的路径,并存储在一个向量或数组中。
3) 遍历这两条路径,直到遇到一个不同的节点,则前面的那个即为最低公共祖先.(相当于寻找两个链表上的最后一个公共节点)
时间复杂度: O(n),
树被遍历了两次,每次遍历复杂度不超过n,然后比较路径。
方法二:从root开始遍历,如果n1和n2中的任一个和root匹配,那么root就是LCA。
如果都不匹配,则分别递归左、右子树,如果有一个 key(n1或n2)出现在左子树,并且另一个key(n1或n2)出现在右子树,则root就是LCA. 如果两个key都出现在左子树,则说明LCA在左子树中,否则在右子树。
时间复杂度为O(n),但是上面的方法还是有所局限的,必须保证两个要查找的节点n1和n2都出现在树中。如果n1不在树中,则会返回n2为LCA,理想答案应该为NULL。要解决这个问题,可以先查找下 n1和n2是否出现在树中,然后加几个判断即可。
情况三:含有指向父节点指针的任意树
思想一:将一个结点回退到父结点,每退一步,另一个结点指针将回退到不能退为止。此过程来判断它们两结点是否有共同的父母。
也可将节点保存在两个数组或链表里,将问题转化为求两个链表的第一个公共节点问题。
Node * NearestCommonAncestor(Node * root,Node * p,Node * q)
{
Node * temp;
while(p!=NULL)
{
p=p->parent;
temp=q;
while(temp!=NULL)
{
if(p==temp->parent)
return p;
temp=temp->parent;
}
}
}
思想二:活用Hash表,因为二重循环中很多都是重复的查询操作:
可以将q到头结点建立一张Hash表,然后从p到头结点,边遍历边查找Hash表,直到第一次在hash表在哦个查找到节点值存在。
(其实我们可以简单的过程来看思想二的算法:我们可以开辟指向节点的指针数组,先从一个节点下手,让它一直回退,每退一步,数组新的位置记录下它,即指向该节点,直到第一个节点回退完,再进行第二个节点的回退,每退一步就检查一下它在数组中有没有,这样和思想一是一样的,故为了加速,这里应该将每一个节点的回退过程的地址扔进hashset里去,在回退第二个节点时,查一下hashset里有没有此节点,有则找到所以的祖先节点,没有就继续找)
情况四:就是一颗普通的树
方法一:从根节点开始遍历一颗树,没遍历一个节点就判断两个输入点是否在它的子树中,如果在子树中,则分别遍历它的所有子节点,并判断两个输入节点是否在他们的子树中,直到找到第一个这样的节点:他的子树中同时包含这两个节点,他所有子节点的子树都不能同时包含这两个输入节点。
这里存在大量的重复遍历,效率不高。
方法二:用两个链表分别保存从根节点到输入的两个结点的路径,然后把问题转换成两个链表的最后公共节点。
方法三:改进方法二
方案二中,观察到两次树结点查找的遍历中,其中一个结点的遍历过的树结点序列将完全覆盖查找另一结点时所遍历的树结点序列。由此入手,本文提出了如下的改进解决方案。
【改进方案】:
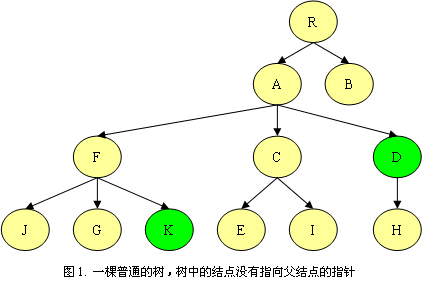
深度优先遍历树,并记录路径,当找到第一个结点后,在当前基础上继续遍历搜索第二个结点,并记录第一个结点路径的变化程度,直到找到第二个结点。最后,根据栈信息和记录的结点路径变化程度得到最低公共祖先。如图1,假设输入的两个树结点为D和K,树的根节点为R,则求D和K的最低公共结点的过程如下表:
从中,可以看到,改进后的方案,只需对树执行一次遍历。而在辅助空间的需求上, 只需使用一个栈(外加少量结点指针变量和1个表示路径变化程度的整型变量)。而且,如果采用递归的方式实现,该栈所需保存的信息,还可以通过递归时的函数调用栈得以保存。
我们从最简单的情况开始分析。
情况一:是二叉树,且是二叉搜索树(二叉排序树,二叉查找树)
分析:由于二叉排序树具有这样的特点:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉排序树。
所以我们只需要从树的根节点开始和输入的两个节点进行比较。如果当前节点的值比两个节点都大,那么最低公共父节点一定在当前节点的左子树中,于是下一步遍历当前节点的左子节点。如果当前节点比两个节点都大,那么最低公共父节点一定在当前节点的右子树中,于是下一步遍历当前节点的右子节点。这样从树中从上到下找到的第一个在输入节点的值之间的节点就是最低公共祖先。
struct
node //二叉树节点数据结构
{
int data;
struct node*
left;
struct node*
right;
};
struct node*
newNode(int );
Node*
findLowerstCommonAncestor(Node* root,int
value1,int value2)
{
while ( root!=
NULL )
{
int value=
root->getValue(); //获取当前节点的值
if ( value>
value1&& value>
value2 ) //当前节点的值大于两输入值
root = root->getLeft();
elseif
(value< value1&&
value< value2) //当前节点的值校园两输入值
root = root->getRight();
else
return root;
}
return NULL;
}
时间复杂度是树的深度,空间复杂度是O(1)。
情况二:是二叉树,但是普通的二叉树


方法一:一个简单的复杂度为
O(n) 的算法,解决LCA问题
1) 找到从根到n1的路径,并存储在一个向量或数组中。
2)找到从根到n2的路径,并存储在一个向量或数组中。
3) 遍历这两条路径,直到遇到一个不同的节点,则前面的那个即为最低公共祖先.(相当于寻找两个链表上的最后一个公共节点)
// O(n) 解决 LCA |
02 | #include <iostream> |
03 | #include <vector> |
04 | using namespace std; |
05 |
06 | //二叉树节点 |
07 | struct Node |
08 | { |
09 | int key; |
10 | struct Node *left, *right; |
11 | }; |
12 | //公用函数,生成一个节点 |
13 | Node * newNode( int k) |
14 | { |
15 | Node *temp = new Node; |
16 | temp->key = k; |
17 | temp->left = temp->right = NULL; |
18 | return temp; |
19 | } |
20 | //找到从root到 节点值为key的路径,存储在path中。没有的话返回-1 |
21 | bool findpath(Node * root,vector< int > &path, int key){ |
22 | if (root == NULL) return false ; |
23 | path.push_back(root->key); |
24 | if (root->key == key) return true ; |
25 | //左子树或右子树 是否找到,找到的话当前节点就在路径中了 |
26 | bool find = ( findpath(root->left, path, key) || findpath(root->right,path ,key) ); |
27 | if (find) return true ; |
28 | //该节点下未找到就弹出 |
29 | path.pop_back(); |
30 | return false ; |
31 | } |
32 |
33 | int findLCA(Node * root, int key1, int key2){ |
34 | vector< int > path1,path2; |
35 | bool find1 = findpath(root, path1, key1); |
36 | bool find2 = findpath(root, path2, key2); |
37 | if (find1
&& find2){ |
38 | int ans ; |
39 | for ( int i=0;
i<path1.size(); i++){ |
40 | if (path1[i]
!= path2[i]){ |
41 | break ; |
42 | } else |
43 | ans = path1[i]; |
44 | } |
45 | return ans; |
46 | } |
47 | return -1; |
48 | } |
49 |
50 | // Driver program to test above functions |
51 | int main() |
52 | { |
53 | // 按照上面的图来创创建树 |
54 | Node * root = newNode(1); |
55 | root->left = newNode(2); |
56 | root->right = newNode(3); |
57 | root->left->left = newNode(4); |
58 | root->left->right = newNode(5); |
59 | root->right->left = newNode(6); |
60 | root->right->right = newNode(7); |
61 | cout << "LCA(4, 5) = " << findLCA(root, 4, 5); |
62 | cout << "\nLCA(4, 6) = " << findLCA(root, 4, 6); |
63 | cout << "\nLCA(3, 4) = " << findLCA(root, 3, 4); |
64 | cout << "\nLCA(2, 4) = " << findLCA(root, 2, 4); |
65 | return 0; |
66 | } |
树被遍历了两次,每次遍历复杂度不超过n,然后比较路径。
方法二:从root开始遍历,如果n1和n2中的任一个和root匹配,那么root就是LCA。
如果都不匹配,则分别递归左、右子树,如果有一个 key(n1或n2)出现在左子树,并且另一个key(n1或n2)出现在右子树,则root就是LCA. 如果两个key都出现在左子树,则说明LCA在左子树中,否则在右子树。
/* 只用一次遍历解决LCA */ |
02 | #include <iostream> |
03 | using namespace std; |
04 | struct Node |
05 | { |
06 | struct Node *left, *right; |
07 | int key; |
08 | }; |
09 | Node* newNode( int key) |
10 | { |
11 | Node *temp = new Node; |
12 | temp->key = key; |
13 | temp->left = temp->right = NULL; |
14 | return temp; |
15 | } |
16 |
17 | // 返回n1和n2的 LCA的指针 |
18 | // 假设n1和n2都出现在树中 |
19 | struct Node *findLCA( struct Node* root, int n1, int n2) |
20 | { |
21 | if (root == NULL) return NULL; |
22 |
23 | // 只要n1 或 n2 的任一个匹配即可 |
24 | // (注意:如果 一个节点是另一个祖先,则返回的是祖先节点。因为递归是要返回到祖先的 ) |
25 | if (root->key == n1 || root->key == n2) |
26 | return root; |
27 | // 分别在左右子树查找 |
28 | Node |
29 | Node |
30 | // 如果都返回非空指针 Non-NULL, 则说明两个节点分别出现了在两个子树中,则当前节点肯定为LCA |
31 | if (left_lca && right_lca) return root; |
32 | // 如果一个为空,在说明LCA在另一个子树 |
33 | return (left_lca != NULL)? left_lca: right_lca; |
34 | } |
35 |
36 | //测试 |
37 | int main() |
38 | { |
39 | // 构造上面图中的树 |
40 | Node * root = newNode(1); |
41 | root->left = newNode(2); |
42 | root->right = newNode(3); |
43 | root->left->left = newNode(4); |
44 | root->left->right = newNode(5); |
45 | root->right->left = newNode(6); |
46 | root->right->right = newNode(7); |
47 | cout << "LCA(4, 5) = " << findLCA(root, 4, 5)->key; |
48 | cout << "\nLCA(4, 6) = " << findLCA(root, 4, 6)->key; |
49 | cout << "\nLCA(3, 4) = " << findLCA(root, 3, 4)->key; |
50 | cout << "\nLCA(2, 4) = " << findLCA(root, 2, 4)->key; |
51 | return 0; |
52 | } |
情况三:含有指向父节点指针的任意树
思想一:将一个结点回退到父结点,每退一步,另一个结点指针将回退到不能退为止。此过程来判断它们两结点是否有共同的父母。
也可将节点保存在两个数组或链表里,将问题转化为求两个链表的第一个公共节点问题。
Node * NearestCommonAncestor(Node * root,Node * p,Node * q)
{
Node * temp;
while(p!=NULL)
{
p=p->parent;
temp=q;
while(temp!=NULL)
{
if(p==temp->parent)
return p;
temp=temp->parent;
}
}
}
思想二:活用Hash表,因为二重循环中很多都是重复的查询操作:
如果每个节点有指向父节点的指针,那么逆向遍历两个节点的所有祖先节点,找第一个一样的祖先,可用hash表存储,
时间复杂度是树的深度,空间复杂度也是数的深度。
可以将q到头结点建立一张Hash表,然后从p到头结点,边遍历边查找Hash表,直到第一次在hash表在哦个查找到节点值存在。
(其实我们可以简单的过程来看思想二的算法:我们可以开辟指向节点的指针数组,先从一个节点下手,让它一直回退,每退一步,数组新的位置记录下它,即指向该节点,直到第一个节点回退完,再进行第二个节点的回退,每退一步就检查一下它在数组中有没有,这样和思想一是一样的,故为了加速,这里应该将每一个节点的回退过程的地址扔进hashset里去,在回退第二个节点时,查一下hashset里有没有此节点,有则找到所以的祖先节点,没有就继续找)
情况四:就是一颗普通的树
方法一:从根节点开始遍历一颗树,没遍历一个节点就判断两个输入点是否在它的子树中,如果在子树中,则分别遍历它的所有子节点,并判断两个输入节点是否在他们的子树中,直到找到第一个这样的节点:他的子树中同时包含这两个节点,他所有子节点的子树都不能同时包含这两个输入节点。
这里存在大量的重复遍历,效率不高。
方法二:用两个链表分别保存从根节点到输入的两个结点的路径,然后把问题转换成两个链表的最后公共节点。
方法三:改进方法二
方案二中,观察到两次树结点查找的遍历中,其中一个结点的遍历过的树结点序列将完全覆盖查找另一结点时所遍历的树结点序列。由此入手,本文提出了如下的改进解决方案。

【改进方案】:
深度优先遍历树,并记录路径,当找到第一个结点后,在当前基础上继续遍历搜索第二个结点,并记录第一个结点路径的变化程度,直到找到第二个结点。最后,根据栈信息和记录的结点路径变化程度得到最低公共祖先。如图1,假设输入的两个树结点为D和K,树的根节点为R,则求D和K的最低公共结点的过程如下表:
| 步骤 | 栈 | 第一个结点 | 第二个结点 | 路径变化程度 |
| 1 | R | — | — | — |
| 2 | R,A | — | — | — |
| 3 | R,A,F | — | — | — |
| 4 | R,A,F,J | — | — | — |
| 5 | R,A,F,G | — | — | — |
| 6 | R,A,F,K | K | — | 0(或K) |
| 7 | R,A,C | K | — | 1(或A) |
| 8 | R,A,C,E | K | — | 2(或A) |
| 9 | R,A,C,I | K | — | 2(或A) |
| 10 | R,A,D | K | D | 1(或A) |
| è 得出结果,最低公共祖先结点为A |
相关文章推荐
- 剑指offer 面试题50—树中两个节点的最低公共祖先
- 面试题50:二叉树中两个节点的最低公共祖先
- 面试题50:树中两个节点的最低公共祖先
- 235. Lowest Common Ancestor of a Binary Search Tree (求二叉树中两个节点的最近公共祖先)
- Lowest Common Ancestor of a Binary Search Tree(树中两个结点的最低公共祖先)
- 235. Lowest Common Ancestor of a Binary Search Tree | 二叉查找树两个节点的最低共同祖先
- 剑指offer 面试题50 树中两个节点的最低公共祖先
- 面试题50_树中两个节点的最低公共祖先
- 面试题50:树中两个节点最低公共祖先
- 寻找二叉树中的最低公共祖先结点----LCA(Lowest Common Ancestor )问题(递归)
- 235. Lowest Common Ancestor of a Binary Search Tree(LCA最低公共祖先)
- 面试题50—树中两个节点的最低公共祖先
- [剑指offer][面试题50]树中两个节点的最低公共祖先
- Tree_Graph LCA(Lowest Common Ancestor) 最低公共节点 (BST或者一般树) @CareerCup
- 剑指Offer:面试题50 树中两个节点的最低公共祖先
- 第19题 在二叉查找树中找到两个结点的最低公共祖先 Lowest Common Ancestor
- 面试题50:树中两个节点的最低公共祖先
- 面试题50 树中两个结点的最低公共祖先
- 【剑指offer】 面试题50: 树中两个结点的最低公共祖先
- 在二叉树中查找两个节点的最近的公共祖先节点(有回溯指针)(NCA--nearest common ancestor)
