斯坦福大学公开课 :机器学习课程(Andrew Ng)——6、监督学习:Support Vector Machine,破
2015-01-04 11:51
399 查看
[b]6)拉格朗日对偶(Lagrange duality)[/b]
[b]7)最优间隔分类器(optimal margin classifier)[/b]
[b]8)核函数(Kernel)[/b]
[b][b]9)核函数的有效性[/b]
[/b]
6)拉格朗日对偶(Lagrange duality)
先抛开上一节的二次规划(最小值)问题。
对于存在等式约束的极值问题求解,通过引入拉格朗日算子构造拉格朗日公式就可以完美解决。
对于存在不等式约束的极值问题求解,如下:

我们定义更一般化的拉格朗日公式:

因为我们求解的是最小值,而这里的
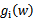
已经不严格等于0,而是小于等于0,我们虽然可以将

调整成很大的正值以使函数的结果是负无穷,但这种“虚假最小值”并不是我们想要的,因此我们为了排除这种情况定义下面的函数:
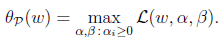
这里的P代表primal。
进一步分析(假设
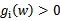
或者
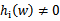
,那么我们总是可以调整
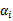
和
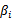
来使得
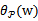
有最大值为正无穷。而只有g和h同时满足约束时,
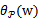
才有最小值f(w),这时gi和hi都等于0。)可知:

这样我们原来要求解的二次规划(最小值)问题min f(w)可以转换成求
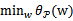
了。而
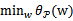
可以进一步转换为:

如果直接求解上式,首先要面对两个参数,且
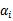
是不等式约束,然后还要在w上求最小值。这个过程不容易做,所以我们引入该问题的对偶形式:

相对于原问题,对偶问题只是更换了min和max的顺序,而一般更换顺序的结果是Max Min(X) <= MinMax(X),即:
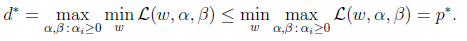
通过引入的对偶形式,我们只要找到
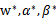
使d*=p*,那么这组
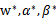
中的W*肯定就是我们原来要求解的二次规划(最小值)问题min
f(w)的解了,那么怎么找这组
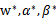
?根据当前知识,我们只知道:假设存在
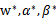
使得
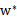
是原问题的解,
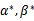
是对偶问题的解,如果
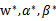
满足了库恩-塔克条件(Karush-Kuhn-Tucker,
KKT condition),那么他们就是原问题和对偶问题的解(即,使原问题和对偶问题等价)。下面给出库恩-塔克条件(Karush-Kuhn-Tucker, KKT condition):
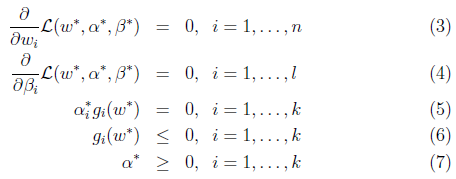
公式(5)称为KKT dual complementarity(KKT对偶互补)条件。这个条件隐含了如果
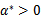
,那么
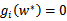
,此时的w*正处于可行域的边界上(正好取到“=0”),之后我们会明白,gi(w)=0才是真正起作用的约束;而其他位于可行域内部(
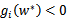
)的点对应的

,之后我们会明白,gi(w)<0都是不起作用的约束。这个KKT双重补足条件会用来解释支持向量和SMO的收敛测试。
KKT的总体思想是:极值会在可行域边界上取得,也就是在不等式等于0的gi(w)约束或等式hi(w)约束里取得,而最优下降方向一般是这些“不等式等于0的gi(w)约束或等式hi(w)约束”的线性组合。对于在可行域边界内(
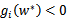
)的点,对最优解不起作用,因此前面的系数

。
7)最优间隔分类器(optimal margin classifier)
上一节中我们只是给出了
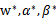
满足KKT条件就是原问题和对偶问题的解的结论,但实际上并没有告诉我们具体怎么求
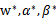
。这里我们仍然不给出具体求解
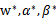
的方法,但只是告诉我们,如果求出了α*(对于α*的具体求解方法,我们交给下一节的SMO算法),那么就可以求出β*,进而求出w*,下面我们看一下这些结论是怎么得到的。
从KKT条件得知只有函数间隔是1(离超平面最近的点)的线性约束式前面的系数
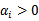
,对应的约束式为
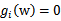
,对于其他的不在线上的点(
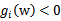
),极值不会在他们所在的范围内取得,因此前面的系数
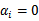
。看下面的图:
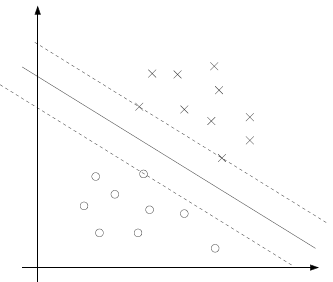
实线是最大间隔超平面,假设×号的是正例,圆圈的是负例。在虚线上的点就是函数间隔是1的点,那么他们前面的系数
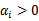
,其他点都是
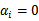
。这三个点称作支持向量。
重新回到SVM的最初优化问题:
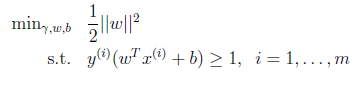
我们将约束条件改写为:
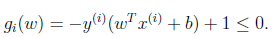
构造拉格朗日函数如下:
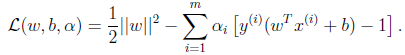
这里只有
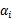
没有
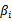
是因为原问题中没有等式约束,只有不等式约束。
下面我们按照对偶问题的求解步骤来一步步进行:
对于对偶问题
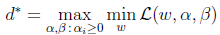
,我们分为最小化

和最大化min
L(w,b,α)两步。
首先求解

的最小值,我们先固定

,那么
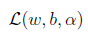
的最小值只与w和b有关,对w和b分别求偏导数:
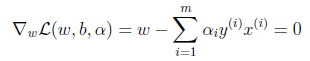
(d1)
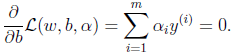
(d2)
化简(d1)得到:
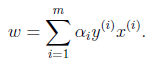
,将该式带回到构造的拉格朗日函数中,化简(化简过程参考:http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982684.html)得到:
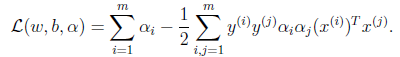
。注意虽然写的是L(w,b,α),实际上却是L(w,b,α)关于自变量w的最小值(目标函数是凸函数)。
接着是极大化上面求得关于自变量w的最小值函数
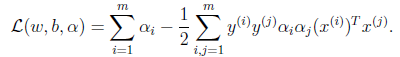
,
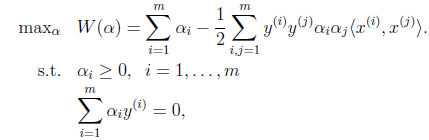
这里我们将向量内积
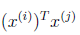
表示为
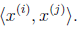
。
其实它是满足KKT条件的,所以,一定存在
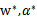
使得
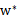
是原问题的解,
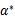
是对偶问题的解。
同样的,
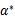
的求解留给下一节的SMO算法。这里仅仅假设已经求出了
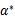
,那么根据
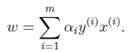
即可求出
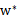
(原问题的解),进而求出
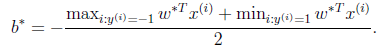
即离超平面最近的正的函数间隔要等于离超平面最近的负的函数间隔。
最后考虑一个“题外话”,将前面求解中得到的
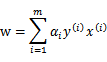
带入
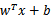
得:
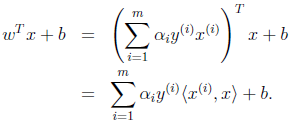
也就是说,以前新来的要分类的样本首先根据w和b做一次线性运算,然后看求的结果是大于0还是小于0来判断是正例还是负例。现在有了
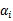
,我们不需要求出w,只需将新来的样本和训练数据中的所有样本做内积和即可。那有人会说,与前面所有的样本都做运算是不是太耗时了?其实不然,我们从KKT条件中得到,只有支持向量的
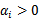
,其他情况
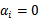
。因此,我们只需求新来的样本和支持向量的内积,然后运算即可。这种写法为下面要提到的核函数(kernel)做了很好的铺垫。
8)核函数(Kernel)
考虑“线性回归”问题,假设我们从样本点的分布中看到x和y符合3次曲线,那么我们希望使用x的三次多项式来逼近这些样本点。那么首先需要将特征x扩展到三维

,然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射(feature
mapping)。映射函数称作

,在这个例子中

我们希望将得到的映射后的特征应用于SVM分类,而不是最初的属性。这样,我们需要将前面

公式中的内积从
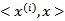
,映射到
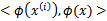
。将核函数形式化定义,如果原始属性内积是
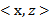
,映射后的特征内积为
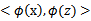
,那么定义核函数(Kernel)为
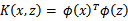
。
除了从属性向特征的映射的角度理解核函数外,领悟核函数的另一种视角是:由于计算的是内积,我们可以想到余弦相似度,如果x和z向量夹角越小,那么核函数值越大,反之,越小。因此,核函数
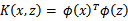
的值可以看做是

和
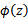
相似度的度量。
到这里,我们可以得出结论,要使用核函数,只需先计算
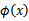
,然后计算
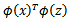
即可,然而这种计算方式是非常低效的,那么我们能不能想办法减少计算时间呢?为了回答这个问题,我们先看一个核函数:
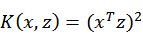
,假设x和z都是n维的,那么展开后得:
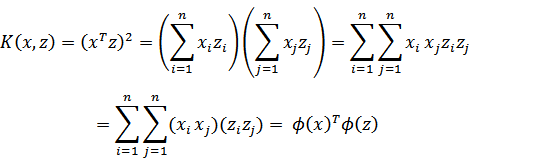
,这个时候发现我们可以只计算原始特征x和z内积的平方(时间复杂度是O(n)),就等价与计算映射后特征的内积,也就是说我们不需要花
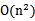
时间了。
另一个经典核函数是:
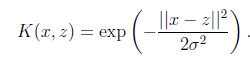
,如果x和z很相近(
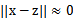
),那么核函数值为1,如果x和z相差很大(
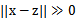
),那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial
Basis Function 简称RBF)。它能够把原始特征映射到无穷维。既然高斯核函数能够比较x和z的相似度,并映射到0到1,回想logistic回归,sigmoid函数可以,因此还有sigmoid核函数等等。
至于为什么需要映射后的特征而不是最初的属性面提到的(从样本点的分布中看到x和y符合3次曲线,能更好拟合)是其中一个原因,另外的一个重要原因是样例可能存在线性不可分的情况,而将属性映射到高维空间后,特征往往就可分了。(在《数据挖掘导论》Pang-Ning Tan等人著的《支持向量机》那一章有个很好的例子说明)。下面有张图说明在低维线性不可分时,映射到高维后就可分了,使用高斯核函数。
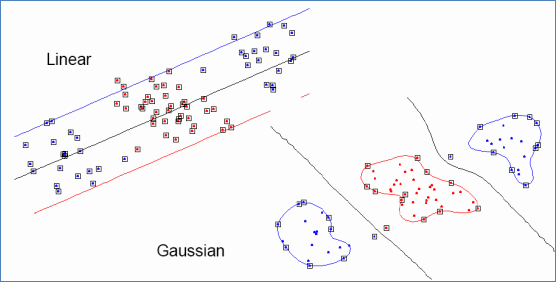
来自Eric Xing的slides
注意,使用核函数后,怎么分类新来的样本呢?线性的时候我们使用SVM学习出w和b,新来样本x的话,我们使用
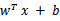
来判断,如果值大于等于1,那么是正类,小于等于1是负类。在两者之间,认为无法确定。如果使用了核函数后,
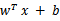
就变成了
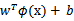
,是否先要找到
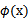
,然后再预测?答案肯定不是了,找
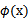
很麻烦,回想上一节说过的
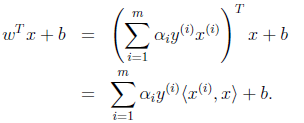
,只需将

替换成
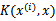
,然后值的判断同上。
9)核函数的有效性
问题:给定一个函数K,我们能否使用K来替代计算
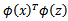
?也就说,对于某个给定的核函数例如
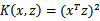
,是否能够找出一个函数映射
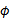
,使得对于所有的x和z,都有
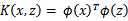
?也可以说,怎样判断给出的核函数K是不是一个有效的核函数(为什么要判断某个核函数是不是有效地呢?因为核函数是我们根据经验和所要处理的问题自己定义的,这就需要我们检验定义的正确性!)。
解决这个问题前,先给出核函数矩阵(Kernel Matrix)的定义:给定m个训练样本
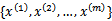
,每一个
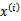
对应一个特征向量,我们将任意两个
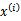
和
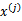
带入核函数K中得到
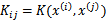
。i可以从1到m,j可以从1到m,这样可以计算出m*m的矩阵K称为核函数矩阵(Kernel
Matrix)。这里,我们将核函数矩阵和核函数都使用K来表示。经过一些列推导我们可以得到:如果K是个有效的核函数(即
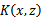
和
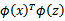
等价),那么,在训练集上得到的核函数矩阵K应该是半正定的(
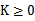
)。
这样我们得到一个核函数的必要条件:K是有效的核函数 ==> 核函数矩阵K是对称半正定的。 其实这个条件也是充分的,由Mercer定理给出:
Mercer定理表明:为了证明K是有效的核函数,那么我们不用去寻找
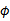
,而只需要在训练集上求出各个
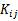
,然后判断矩阵K是否是半正定(使用左上角主子式大于等于零等方法)即可。
最后说明一点,核函数不仅仅用在SVM上,但凡在一个模型后算法中出现了
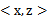
,我们都可以常使用
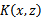
去替换,这可能能够很好地改善我们的算法。
参考:
http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982684.html http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html
[b]7)最优间隔分类器(optimal margin classifier)[/b]
[b]8)核函数(Kernel)[/b]
[b][b]9)核函数的有效性[/b]
[/b]
6)拉格朗日对偶(Lagrange duality)
先抛开上一节的二次规划(最小值)问题。
对于存在等式约束的极值问题求解,通过引入拉格朗日算子构造拉格朗日公式就可以完美解决。
对于存在不等式约束的极值问题求解,如下:

我们定义更一般化的拉格朗日公式:

因为我们求解的是最小值,而这里的
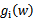
已经不严格等于0,而是小于等于0,我们虽然可以将

调整成很大的正值以使函数的结果是负无穷,但这种“虚假最小值”并不是我们想要的,因此我们为了排除这种情况定义下面的函数:
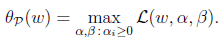
这里的P代表primal。
进一步分析(假设
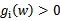
或者
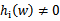
,那么我们总是可以调整
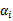
和
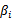
来使得
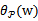
有最大值为正无穷。而只有g和h同时满足约束时,
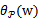
才有最小值f(w),这时gi和hi都等于0。)可知:

这样我们原来要求解的二次规划(最小值)问题min f(w)可以转换成求
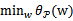
了。而
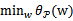
可以进一步转换为:

如果直接求解上式,首先要面对两个参数,且
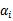
是不等式约束,然后还要在w上求最小值。这个过程不容易做,所以我们引入该问题的对偶形式:

相对于原问题,对偶问题只是更换了min和max的顺序,而一般更换顺序的结果是Max Min(X) <= MinMax(X),即:
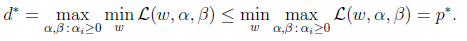
通过引入的对偶形式,我们只要找到
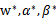
使d*=p*,那么这组
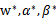
中的W*肯定就是我们原来要求解的二次规划(最小值)问题min
f(w)的解了,那么怎么找这组
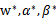
?根据当前知识,我们只知道:假设存在
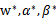
使得
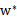
是原问题的解,
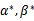
是对偶问题的解,如果
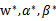
满足了库恩-塔克条件(Karush-Kuhn-Tucker,
KKT condition),那么他们就是原问题和对偶问题的解(即,使原问题和对偶问题等价)。下面给出库恩-塔克条件(Karush-Kuhn-Tucker, KKT condition):
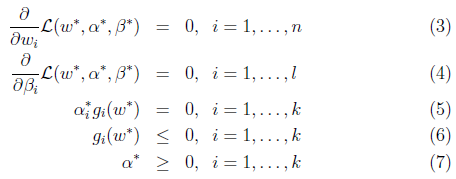
公式(5)称为KKT dual complementarity(KKT对偶互补)条件。这个条件隐含了如果
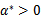
,那么
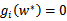
,此时的w*正处于可行域的边界上(正好取到“=0”),之后我们会明白,gi(w)=0才是真正起作用的约束;而其他位于可行域内部(
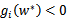
)的点对应的

,之后我们会明白,gi(w)<0都是不起作用的约束。这个KKT双重补足条件会用来解释支持向量和SMO的收敛测试。
KKT的总体思想是:极值会在可行域边界上取得,也就是在不等式等于0的gi(w)约束或等式hi(w)约束里取得,而最优下降方向一般是这些“不等式等于0的gi(w)约束或等式hi(w)约束”的线性组合。对于在可行域边界内(
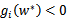
)的点,对最优解不起作用,因此前面的系数

。
7)最优间隔分类器(optimal margin classifier)
上一节中我们只是给出了
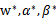
满足KKT条件就是原问题和对偶问题的解的结论,但实际上并没有告诉我们具体怎么求
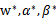
。这里我们仍然不给出具体求解
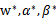
的方法,但只是告诉我们,如果求出了α*(对于α*的具体求解方法,我们交给下一节的SMO算法),那么就可以求出β*,进而求出w*,下面我们看一下这些结论是怎么得到的。
从KKT条件得知只有函数间隔是1(离超平面最近的点)的线性约束式前面的系数
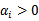
,对应的约束式为
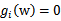
,对于其他的不在线上的点(
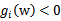
),极值不会在他们所在的范围内取得,因此前面的系数
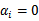
。看下面的图:

实线是最大间隔超平面,假设×号的是正例,圆圈的是负例。在虚线上的点就是函数间隔是1的点,那么他们前面的系数
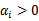
,其他点都是
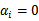
。这三个点称作支持向量。
重新回到SVM的最初优化问题:
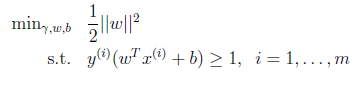
我们将约束条件改写为:
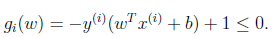
构造拉格朗日函数如下:
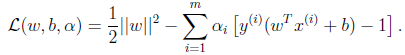
这里只有
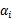
没有
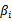
是因为原问题中没有等式约束,只有不等式约束。
下面我们按照对偶问题的求解步骤来一步步进行:
对于对偶问题
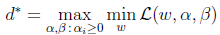
,我们分为最小化

和最大化min
L(w,b,α)两步。
首先求解

的最小值,我们先固定

,那么
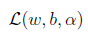
的最小值只与w和b有关,对w和b分别求偏导数:
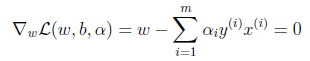
(d1)
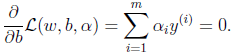
(d2)
化简(d1)得到:
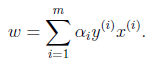
,将该式带回到构造的拉格朗日函数中,化简(化简过程参考:http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982684.html)得到:
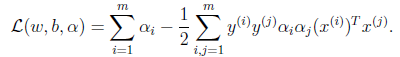
。注意虽然写的是L(w,b,α),实际上却是L(w,b,α)关于自变量w的最小值(目标函数是凸函数)。
接着是极大化上面求得关于自变量w的最小值函数
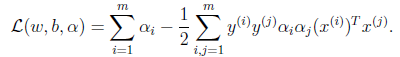
,
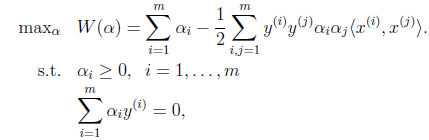
这里我们将向量内积
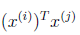
表示为
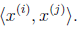
。
其实它是满足KKT条件的,所以,一定存在
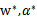
使得
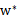
是原问题的解,
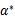
是对偶问题的解。
同样的,
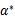
的求解留给下一节的SMO算法。这里仅仅假设已经求出了
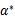
,那么根据
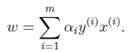
即可求出
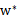
(原问题的解),进而求出
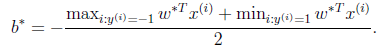
即离超平面最近的正的函数间隔要等于离超平面最近的负的函数间隔。
最后考虑一个“题外话”,将前面求解中得到的
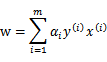
带入
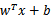
得:
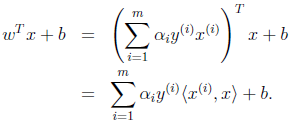
也就是说,以前新来的要分类的样本首先根据w和b做一次线性运算,然后看求的结果是大于0还是小于0来判断是正例还是负例。现在有了
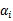
,我们不需要求出w,只需将新来的样本和训练数据中的所有样本做内积和即可。那有人会说,与前面所有的样本都做运算是不是太耗时了?其实不然,我们从KKT条件中得到,只有支持向量的
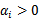
,其他情况
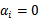
。因此,我们只需求新来的样本和支持向量的内积,然后运算即可。这种写法为下面要提到的核函数(kernel)做了很好的铺垫。
8)核函数(Kernel)
考虑“线性回归”问题,假设我们从样本点的分布中看到x和y符合3次曲线,那么我们希望使用x的三次多项式来逼近这些样本点。那么首先需要将特征x扩展到三维

,然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射(feature
mapping)。映射函数称作

,在这个例子中

我们希望将得到的映射后的特征应用于SVM分类,而不是最初的属性。这样,我们需要将前面

公式中的内积从
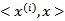
,映射到
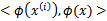
。将核函数形式化定义,如果原始属性内积是
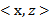
,映射后的特征内积为
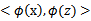
,那么定义核函数(Kernel)为
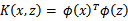
。
除了从属性向特征的映射的角度理解核函数外,领悟核函数的另一种视角是:由于计算的是内积,我们可以想到余弦相似度,如果x和z向量夹角越小,那么核函数值越大,反之,越小。因此,核函数
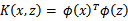
的值可以看做是

和
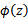
相似度的度量。
到这里,我们可以得出结论,要使用核函数,只需先计算
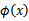
,然后计算
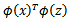
即可,然而这种计算方式是非常低效的,那么我们能不能想办法减少计算时间呢?为了回答这个问题,我们先看一个核函数:
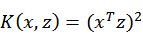
,假设x和z都是n维的,那么展开后得:
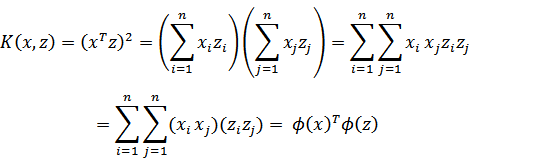
,这个时候发现我们可以只计算原始特征x和z内积的平方(时间复杂度是O(n)),就等价与计算映射后特征的内积,也就是说我们不需要花
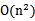
时间了。
另一个经典核函数是:
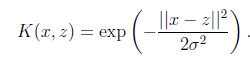
,如果x和z很相近(
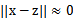
),那么核函数值为1,如果x和z相差很大(
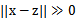
),那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial
Basis Function 简称RBF)。它能够把原始特征映射到无穷维。既然高斯核函数能够比较x和z的相似度,并映射到0到1,回想logistic回归,sigmoid函数可以,因此还有sigmoid核函数等等。
至于为什么需要映射后的特征而不是最初的属性面提到的(从样本点的分布中看到x和y符合3次曲线,能更好拟合)是其中一个原因,另外的一个重要原因是样例可能存在线性不可分的情况,而将属性映射到高维空间后,特征往往就可分了。(在《数据挖掘导论》Pang-Ning Tan等人著的《支持向量机》那一章有个很好的例子说明)。下面有张图说明在低维线性不可分时,映射到高维后就可分了,使用高斯核函数。

来自Eric Xing的slides
注意,使用核函数后,怎么分类新来的样本呢?线性的时候我们使用SVM学习出w和b,新来样本x的话,我们使用
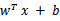
来判断,如果值大于等于1,那么是正类,小于等于1是负类。在两者之间,认为无法确定。如果使用了核函数后,
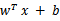
就变成了
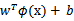
,是否先要找到
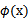
,然后再预测?答案肯定不是了,找
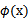
很麻烦,回想上一节说过的
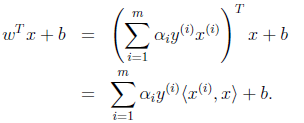
,只需将

替换成
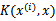
,然后值的判断同上。
9)核函数的有效性
问题:给定一个函数K,我们能否使用K来替代计算
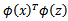
?也就说,对于某个给定的核函数例如
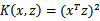
,是否能够找出一个函数映射
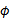
,使得对于所有的x和z,都有
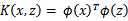
?也可以说,怎样判断给出的核函数K是不是一个有效的核函数(为什么要判断某个核函数是不是有效地呢?因为核函数是我们根据经验和所要处理的问题自己定义的,这就需要我们检验定义的正确性!)。
解决这个问题前,先给出核函数矩阵(Kernel Matrix)的定义:给定m个训练样本
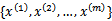
,每一个
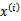
对应一个特征向量,我们将任意两个
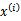
和
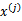
带入核函数K中得到
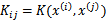
。i可以从1到m,j可以从1到m,这样可以计算出m*m的矩阵K称为核函数矩阵(Kernel
Matrix)。这里,我们将核函数矩阵和核函数都使用K来表示。经过一些列推导我们可以得到:如果K是个有效的核函数(即
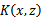
和
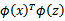
等价),那么,在训练集上得到的核函数矩阵K应该是半正定的(
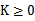
)。
这样我们得到一个核函数的必要条件:K是有效的核函数 ==> 核函数矩阵K是对称半正定的。 其实这个条件也是充分的,由Mercer定理给出:
| Mercer定理: 如果函数K是 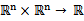 上的映射(也就是从两个n维向量映射到实数域)。那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例 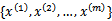 ,其相应的核函数矩阵是对称半正定的。 |
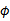
,而只需要在训练集上求出各个
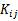
,然后判断矩阵K是否是半正定(使用左上角主子式大于等于零等方法)即可。
最后说明一点,核函数不仅仅用在SVM上,但凡在一个模型后算法中出现了
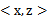
,我们都可以常使用
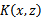
去替换,这可能能够很好地改善我们的算法。
参考:
http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982684.html http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html
相关文章推荐
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——5、监督学习:Support Vector Machine,引
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——7、监督学习:Support Vector Machine,立
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——10、无监督学习:Mixture of Gaussians and the EM Algorithm
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——3、监督学习:Gaussian Discriminant Analysis (GDA)
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——12、无监督学习:Factor Analysis
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——8、监督学习:Learning Theory
- 斯坦福大学公开课机器学习课程(Andrew Ng)二监督学习应用 梯度下降
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——4、监督学习:Naive Bayes
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——11、无监督学习:the derivation of EM Algorithm
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——14、无监督学习:Independent Component Analysis(ICA)
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——2、监督学习:Regression and Classification
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——9、无监督学习:K-means Clustering Algorithm
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——15、无监督学习:Reinforcement Learning and Control
- 机器学习技法课程学习笔记3 -- Kernel Support Vector Machine
- 台湾大学林轩田机器学习技法课程学习笔记2 -- Dual Support Vector Machine
- 机器学习技法课程学习笔记1 -- Linear Support Vector Machine
- 机器学习技法课程学习笔记2 -- Dual Support Vector Machine
- 台湾大学林轩田机器学习技法课程学习笔记1 -- Linear Support Vector Machine
- 机器学习第五篇(stanford大学公开课学习笔记) —支持向量机(Support Vector Machine)
