斯坦福大学公开课 :机器学习课程(Andrew Ng)——5、监督学习:Support Vector Machine,引
2015-01-03 21:40
381 查看
[b]1)简单说明[/b]
[b]2)再说logistic回归[/b]
[b][b]3)支持向量机的假设表示[/b][/b]
4)函数间隔(functional margin)和几何间隔(geometric margin)
4.1)函数间隔
4.2)几何间隔
5)最优间隔分类器(optimal margin classifier)
6)简单总结
1)简单说明
支持向量机基本上是最好的有监督学习算法了。Andrew Ng老师从前几节讲的logistic回归出发,引出了SVM,既揭示了模型间的联系,也让人觉得过渡更自然。
2)再说logistic回归
Logistic回归模型是将特性的线性组合作为自变量(该自变量的取值范围是负无穷到正无穷),并利用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
假设函数
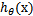
为:

,其中,logistic函数为:
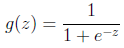
而假设函数就是特征属于y=1的概率:
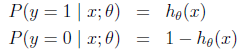
。
当我们要判别一个新来的特征属于哪个类时,只需求
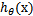
,若
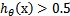
就是y=1的类,反之属于y=0类。对应到g(z),我们发现g(z)只不过是用来映射,真实的类别决定权还在

。还有当
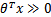
时,
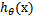
=1,反之
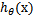
=0。Logistic回归就是要学习得到
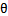
,使训练数据中y=1的特征
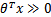
,而是y=0的特征
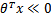
,但是强调在全部训练实例上达到这个目标。
图形化表示如下:
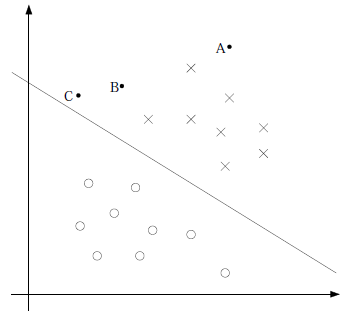
中间那条线是
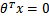
,logistic回顾强调所有点尽可能地远离中间那条线,学习出的结果也就中间那条线。
从图中我们可以确定A是×类别的,然而C我们是不太确定的,B还算能够确定;这间接地告诉我们:我们更应该关心靠近中间分割线的点,让他们尽可能地远离中间线,而不是在所有点上达到最优。考虑针对所有点的最优解(即学习到的分割线)会使一部分点(这些点往往更类似于C的位置)靠近中间线来换取另外一部分点(这些点往往更类似于A的位置)更加远离中间线,但就像刚才说的,我们实际不关心A离分割线有多远,而更关心C离分界线有多远,这样一想就知道logistic回归考虑针对所有点的最优解(即学习到的分割线)其实还是有一点点缺点的,这就是支持向量机要弥补的地方!即,支持向量机考虑局部最优解(只关心离分割线最近的某些点,不关心已经有明确分类的远离分割线的点),logistic回归考虑全局最优解(通过调整中间线,往往会使已经远离的点使其更加远离,造成“虚假最优”,但没考虑到调整中间线会使很多分类不明确的靠近点更加靠近)。这是我的个人直观理解。
3)支持向量机的假设表示
a)结果标签由logistic回归中的y=0,y=1改为y=-1,y=1。
b)同时将
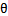
替换成w和b。以前的
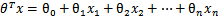
,其中认为
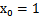
。现在我们替换
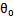
为b,替换
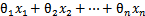
为

(即
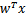
)。即,
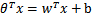
。
所以,新的假设函数
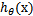
为:
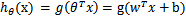
。也就是说除了a)b)中提到的标记不同外,与logistic回归没有任何区别。将假设函数表示为w和b的函数即:
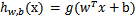
上一节提到只需考虑
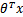
的正负问题,而不用关心g(z)的具体形式,因此我们在这里将
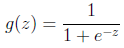
做一个简化,从原来将自变量z映射到(0,1)上改为直接映射到y=-1和y=1上。即,映射关系如下(此时的类别决定权仍然是在z,即
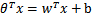
,而不是g(z)函数):
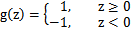
4)函数间隔(functional margin)和几何间隔(geometric margin)
4.1)函数间隔
定义针对某一个样本的函数间隔如下:
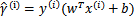
。
可想而知,当

时,根据上节g(z)的定义,
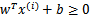
,

的值实际上就是
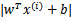
。反之亦然。为了使函数间隔最大(更大的信心确定该例是正例还是反例),当
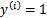
时,
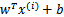
应该是个大正数,反之是个大负数。因此函数间隔代表了我们认为特征是正例还是反例的确信度。
但是,如果同时加大w和b,比如在
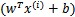
前面乘个系数2,那么所有点的函数间隔都会增大二倍,然而我们要求的解(即直线

)并没有因为函数间隔的增大增强分类效果,而是毫无变化。这就要求我们通过归一化条件防止函数间隔的这种“虚假增大”,因为我们的目标是确定唯一一个w和b,而不是多组线性相关的向量。
我们同时定义针对全局样本的函数间隔如下:
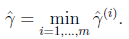
。
4.2)几何间隔
先看图
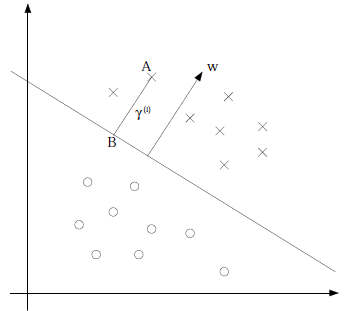
假设我们有了B点所在的
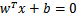
分割面。任何其他一点,比如A到该面的距离以
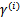
表示,假设B就是A在分割面上的投影。我们知道向量BA的方向是
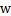
(分割面的梯度),单位向量是
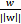
。A点是
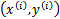
,所以B点是x=
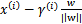
(利用初中的几何知识),带入B点所在的分割面
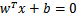
得:
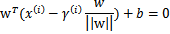
化简得:
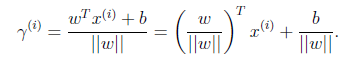
再换种更加优雅的写法:
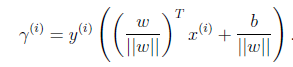
。
当

时,就是函数间隔!也就是说,前面提到的函数间隔归一化结果就是几何间隔:
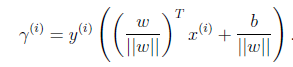
。
他们为什么会一样呢?因为函数间隔是我们定义(认为规定)的,在定义的时候就有几何间隔的色彩。几何间隔的好处是:只要w和b不同时扩大或缩小某个因子,几何间隔能够完成像函数间隔那样的调整分界线

的功能;若w和b同时扩大或缩小某个因子,几何间隔也不会出现像函数间隔那样的“虚假增大”(因为w扩大几倍,
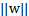
跟着扩大几倍,
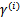
结果无影响),这就解决了函数间隔的问题!
我们同时定义针对全局样本的几何间隔如下:
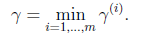
5)最优间隔分类器(optimal margin classifier)
我们的目标是寻找一个超平面,使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面,我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。由上一节我们知道,几何间隔比函数间隔更实用,所以我们希望用几何间隔gama来表示我们的目标,即最大化gama:
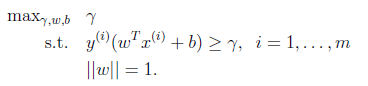
,这里用
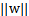
=1规约w,正是为了让
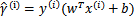
是几何间隔。
由于
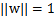
不是凸函数,求解w和b会比较困难,我们想先处理转化一下,考虑几何间隔和函数间隔的关系,
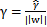
,我们改写一下上面的式子为:
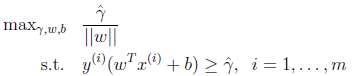
,这时候其实我们求的最大值仍然是几何间隔,只不过此时的w不受
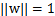
的约束了。
然而这个时候目标函数仍然不是凸函数,我们还要改写。前面说到同时扩大w和b对结果没有影响,但我们最后要求的仍然是w和b的确定值,不是他们的一组倍数值,因此,我们需要对
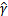
做一些限制,以保证我们解是唯一的。这里为了简便我们取
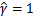
,即将全局的函数间隔定义为1,也就是将离超平面最近的点的距离定义为
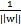
(根据上式中的“>=号”想一想为什么是最近的点!)。由于求
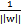
的最大值相当于求

的最小值,因此改写后结果为:
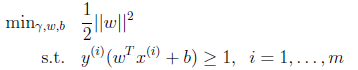
,这下只有线性约束了,而且是个典型的二次规划问题(目标函数是自变量的二次函数),很易求解。
6)简单总结
到这里发现,这个讲义虽然没有像其他讲义一样先画好图,画好分类超平面,在图上标示出间隔那么直观,但每一步推导有理有据,依靠思路的流畅性来推导出目标函数和约束。
到此,我们已经将模型定义出来了。如果求得了w和b,那么来一个特征x,我们就能够分类了,称为最优间隔分类器。接下的问题就是如何求解w和b的问题了。
参考:http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982684.html
[b]2)再说logistic回归[/b]
[b][b]3)支持向量机的假设表示[/b][/b]
4)函数间隔(functional margin)和几何间隔(geometric margin)
4.1)函数间隔
4.2)几何间隔
5)最优间隔分类器(optimal margin classifier)
6)简单总结
1)简单说明
支持向量机基本上是最好的有监督学习算法了。Andrew Ng老师从前几节讲的logistic回归出发,引出了SVM,既揭示了模型间的联系,也让人觉得过渡更自然。
2)再说logistic回归
Logistic回归模型是将特性的线性组合作为自变量(该自变量的取值范围是负无穷到正无穷),并利用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
假设函数
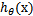
为:

,其中,logistic函数为:
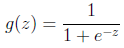
而假设函数就是特征属于y=1的概率:
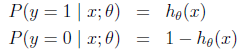
。
当我们要判别一个新来的特征属于哪个类时,只需求
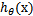
,若
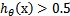
就是y=1的类,反之属于y=0类。对应到g(z),我们发现g(z)只不过是用来映射,真实的类别决定权还在

。还有当
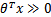
时,
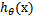
=1,反之
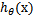
=0。Logistic回归就是要学习得到
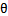
,使训练数据中y=1的特征
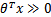
,而是y=0的特征
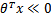
,但是强调在全部训练实例上达到这个目标。
图形化表示如下:

中间那条线是
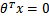
,logistic回顾强调所有点尽可能地远离中间那条线,学习出的结果也就中间那条线。
从图中我们可以确定A是×类别的,然而C我们是不太确定的,B还算能够确定;这间接地告诉我们:我们更应该关心靠近中间分割线的点,让他们尽可能地远离中间线,而不是在所有点上达到最优。考虑针对所有点的最优解(即学习到的分割线)会使一部分点(这些点往往更类似于C的位置)靠近中间线来换取另外一部分点(这些点往往更类似于A的位置)更加远离中间线,但就像刚才说的,我们实际不关心A离分割线有多远,而更关心C离分界线有多远,这样一想就知道logistic回归考虑针对所有点的最优解(即学习到的分割线)其实还是有一点点缺点的,这就是支持向量机要弥补的地方!即,支持向量机考虑局部最优解(只关心离分割线最近的某些点,不关心已经有明确分类的远离分割线的点),logistic回归考虑全局最优解(通过调整中间线,往往会使已经远离的点使其更加远离,造成“虚假最优”,但没考虑到调整中间线会使很多分类不明确的靠近点更加靠近)。这是我的个人直观理解。
3)支持向量机的假设表示
a)结果标签由logistic回归中的y=0,y=1改为y=-1,y=1。
b)同时将
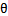
替换成w和b。以前的
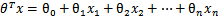
,其中认为
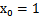
。现在我们替换
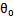
为b,替换
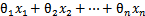
为

(即
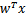
)。即,
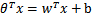
。
所以,新的假设函数
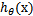
为:
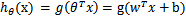
。也就是说除了a)b)中提到的标记不同外,与logistic回归没有任何区别。将假设函数表示为w和b的函数即:
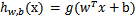
上一节提到只需考虑
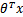
的正负问题,而不用关心g(z)的具体形式,因此我们在这里将
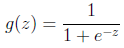
做一个简化,从原来将自变量z映射到(0,1)上改为直接映射到y=-1和y=1上。即,映射关系如下(此时的类别决定权仍然是在z,即
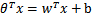
,而不是g(z)函数):
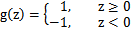
4)函数间隔(functional margin)和几何间隔(geometric margin)
4.1)函数间隔
定义针对某一个样本的函数间隔如下:
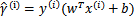
。
可想而知,当

时,根据上节g(z)的定义,
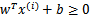
,

的值实际上就是
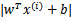
。反之亦然。为了使函数间隔最大(更大的信心确定该例是正例还是反例),当
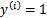
时,
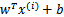
应该是个大正数,反之是个大负数。因此函数间隔代表了我们认为特征是正例还是反例的确信度。
但是,如果同时加大w和b,比如在
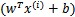
前面乘个系数2,那么所有点的函数间隔都会增大二倍,然而我们要求的解(即直线

)并没有因为函数间隔的增大增强分类效果,而是毫无变化。这就要求我们通过归一化条件防止函数间隔的这种“虚假增大”,因为我们的目标是确定唯一一个w和b,而不是多组线性相关的向量。
我们同时定义针对全局样本的函数间隔如下:
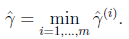
。
4.2)几何间隔
先看图

假设我们有了B点所在的
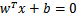
分割面。任何其他一点,比如A到该面的距离以
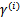
表示,假设B就是A在分割面上的投影。我们知道向量BA的方向是
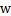
(分割面的梯度),单位向量是
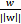
。A点是
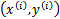
,所以B点是x=
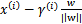
(利用初中的几何知识),带入B点所在的分割面
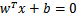
得:
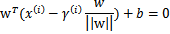
化简得:
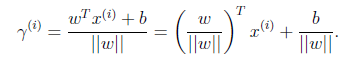
再换种更加优雅的写法:
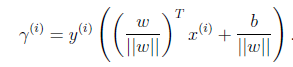
。
当

时,就是函数间隔!也就是说,前面提到的函数间隔归一化结果就是几何间隔:
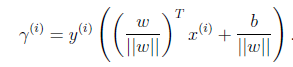
。
他们为什么会一样呢?因为函数间隔是我们定义(认为规定)的,在定义的时候就有几何间隔的色彩。几何间隔的好处是:只要w和b不同时扩大或缩小某个因子,几何间隔能够完成像函数间隔那样的调整分界线

的功能;若w和b同时扩大或缩小某个因子,几何间隔也不会出现像函数间隔那样的“虚假增大”(因为w扩大几倍,
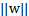
跟着扩大几倍,
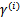
结果无影响),这就解决了函数间隔的问题!
我们同时定义针对全局样本的几何间隔如下:
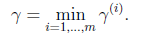
5)最优间隔分类器(optimal margin classifier)
我们的目标是寻找一个超平面,使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面,我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。由上一节我们知道,几何间隔比函数间隔更实用,所以我们希望用几何间隔gama来表示我们的目标,即最大化gama:
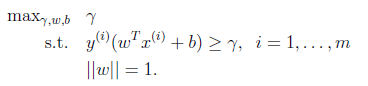
,这里用
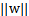
=1规约w,正是为了让
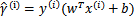
是几何间隔。
由于
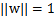
不是凸函数,求解w和b会比较困难,我们想先处理转化一下,考虑几何间隔和函数间隔的关系,
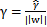
,我们改写一下上面的式子为:
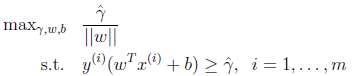
,这时候其实我们求的最大值仍然是几何间隔,只不过此时的w不受
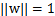
的约束了。
然而这个时候目标函数仍然不是凸函数,我们还要改写。前面说到同时扩大w和b对结果没有影响,但我们最后要求的仍然是w和b的确定值,不是他们的一组倍数值,因此,我们需要对
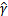
做一些限制,以保证我们解是唯一的。这里为了简便我们取
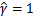
,即将全局的函数间隔定义为1,也就是将离超平面最近的点的距离定义为
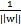
(根据上式中的“>=号”想一想为什么是最近的点!)。由于求
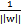
的最大值相当于求

的最小值,因此改写后结果为:
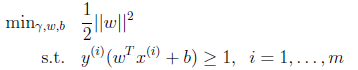
,这下只有线性约束了,而且是个典型的二次规划问题(目标函数是自变量的二次函数),很易求解。
6)简单总结
到这里发现,这个讲义虽然没有像其他讲义一样先画好图,画好分类超平面,在图上标示出间隔那么直观,但每一步推导有理有据,依靠思路的流畅性来推导出目标函数和约束。
到此,我们已经将模型定义出来了。如果求得了w和b,那么来一个特征x,我们就能够分类了,称为最优间隔分类器。接下的问题就是如何求解w和b的问题了。
参考:http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982684.html
相关文章推荐
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——6、监督学习:Support Vector Machine,破
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——7、监督学习:Support Vector Machine,立
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——10、无监督学习:Mixture of Gaussians and the EM Algorithm
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——3、监督学习:Gaussian Discriminant Analysis (GDA)
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——12、无监督学习:Factor Analysis
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——8、监督学习:Learning Theory
- 斯坦福大学公开课机器学习课程(Andrew Ng)二监督学习应用 梯度下降
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——4、监督学习:Naive Bayes
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——11、无监督学习:the derivation of EM Algorithm
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——14、无监督学习:Independent Component Analysis(ICA)
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——2、监督学习:Regression and Classification
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——9、无监督学习:K-means Clustering Algorithm
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)
- 斯坦福大学公开课 :机器学习课程(Andrew Ng)——15、无监督学习:Reinforcement Learning and Control
- 机器学习技法课程学习笔记3 -- Kernel Support Vector Machine
- 台湾大学林轩田机器学习技法课程学习笔记2 -- Dual Support Vector Machine
- 机器学习技法课程学习笔记1 -- Linear Support Vector Machine
- 机器学习技法课程学习笔记2 -- Dual Support Vector Machine
- 台湾大学林轩田机器学习技法课程学习笔记1 -- Linear Support Vector Machine
- 机器学习第五篇(stanford大学公开课学习笔记) —支持向量机(Support Vector Machine)
