关于堆
2022-05-27 16:18
1301 查看
今天讲的堆,简单记录一下:
堆,是一棵完全二叉树,因此设当前节点编号为 i,则其父结点编号为 i/2,左儿子编号为 2*i,右儿子编号为 2i+1
堆有两种比较特别:
一种是大根堆,一种是小根堆
由他们朴实的名字可知,大根堆就是每个节点都小于父亲节点的堆,小根堆反之。
关于堆的操作有两个比较常用的,一个是put(),另一个是get()。
put()算法介绍:
put操作就是往堆里插入一个元素,我们如果硬插的话会有悖于堆的性质,所以要用能够维护堆的方法:
拿小根堆举例:在堆的末尾加入元素,并将该节点当成当前节点。然后比较当前节点与他的父亲的大小,如果当前节点小于其父节点。就将这两个节点位置互换,并持续此操作,直到当前节点不小于其父节点(等于不等于的都可以),以维护小根堆的性质,大根堆亦然。
代码如下:
void put(int d)//展示的是小根堆的操作,大根堆亦然
{
int son,pa;
heap[++heap_size]=d;
son=heap_size;
while(son>1)//到头了就不能继续了
{
pa=son>>2;
if(heap[son]>=heap[pa])//如果儿子本来就比他爹大,满足性质,直接break;
{
break;
}
swap(heap[son],heap[pa]);//将爹与儿子进行交换
son=pa;//让儿子的编号变成他爹的,再进行下一步操作
}
}
当然,使用C++的标准模板库STL也是可以的:
#include<algorithm>//别忘了加STL的头文件
void put(int d)
{
heap[++heap_size]=d;
push_heap(heap+1,heap+heap_size+1,greater<int>());//小根堆
push_heap(heap+1,heap+heap_size+1);//大根堆
}
get()算法介绍:
put就是从堆中取出并删除元素的操作:
拿小根堆举例:
先将堆的根节点与堆尾元素互换,接着将对堆中元素的个数减1.
接着将当前的根节点视作pa比较他的两个儿子的大小(如果他有两个儿子)并选出较小的那个与父亲互换,一直持续此操作,直到又变成一个新的小根堆。大根堆亦然。
代码如下:
int get()//This is 小根堆
{
int pa,son,res;
res=heap[1];//堆顶马上就要离开了,赶紧记录一下
heap[1]=heap[heap_size--];//先将堆顶的元素与堆尾的元素进行交换,再将堆中元素个数减一
pa=1;
while(pa*2<=heap_size)//父亲是不能变成叶节点的欧
{
son=pa*2;
if(son<heap_size && heap[son+1]<heap[son])//为了取最小的孩子
{
son++;
}
if(heap[pa]<=heap[son]) break;
swap(heap[pa],heap[son]);
pa=son;
}
return res;
}
还有就是C++标准模板库的STL:
#include<algorithm>
int get()
{
pop_heap(heap+1,heap+heap_size+1,greater<int>());//小根堆
pop_heap(heap+1,heap+heap_size+1);//大根堆
return heap[heap_size--];
}
我们由此可以将其运用起来:
1、堆排序:
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int heap_size,n;
int heap[100001];
void swap(int &a,int &b)
{
int t=a;
a=b;
b=t;
}
void put(int d)
{
heap[++heap_size]=d;
push_heap(heap+1,heap+heap_size+1,greater<int>());
}
int get()
{
pop_heap(heap+1,heap+heap_size+1,greater<int>());//小根堆
return heap[heap_size--];
}
int ans;
void work()
{
int x,y;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x;
put(x);
}
for(int i=1;i<=n;i++)
{
cout<<get()<<' ';
}
}
int main()
{
work();
return 0;
}
2、合并果子
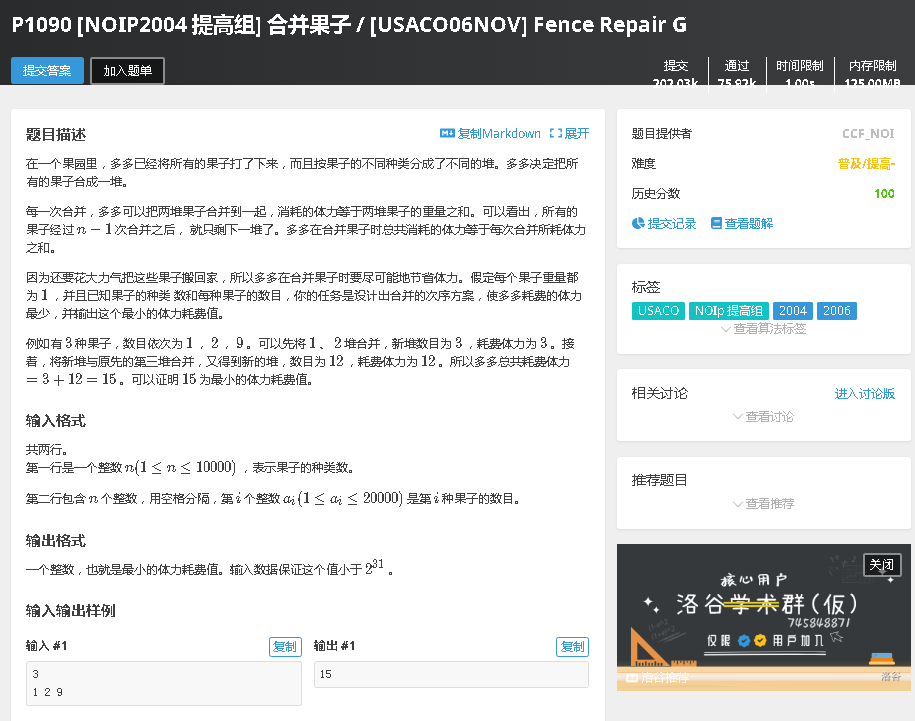
其实就是将堆进行排序,将头两个元素相加成一个元素并放在堆尾,ans+=两数之和:
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int heap_size,n;
int heap[100001];
void swap(int &a,int &b)
{
int t=a;
a=b;
b=t;
}
void put(int d)
{
heap[++heap_size]=d;
push_heap(heap+1,heap+heap_size+1,greater<int>());
}
int get()
{
pop_heap(heap+1,heap+heap_size+1,greater<int>());//小根堆
return heap[heap_size--];
}
int ans;
void work()
{
int x,y;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x;
put(x);
}
for(int i=1;i<n;i++)
{
x=get();
y=get();
ans+=x+y;
put(x+y);
}
cout<<ans;
}
int main()
{
ios::sync_with_stdio(false);
work();
return 0;
}
就先到这吧,再见啦!
相关文章推荐
- 关于java的集合类,以及HashMap中Set的用法!
- 关于char, wchar_t, TCHAR, _T(),L,宏 _T、TEXT,_TEXT、L
- php 关于时间范围的一些封装
- 关于为什么类的静态成员变量不能立即初始化
- 关于vim编辑器
- 假期关于产品-设计-逻辑-市场-团队思考节选30篇
- [转]关于oracle with as用法
- Android关于View的MeasureSpec详解
- 关于编程语言
- 关于C#中的DateTime类型的细节问题
- [转]关于java的内部类。
- 关于Java中Exception类的一些方法
- 你认为人类最大 的缺点是什么?--关于知乎上回答的思考
- 20161018phpmyadmin关于登录的设置
- 关于Qt 5-MSVC 2015 64位在 win7 64位系统debug程序崩溃的问题
- 关于HTTP请求报文和响应报文学习笔记
- 关于mysql数据库中,连续签到等连续日期的处理
- 关于oracle 定时JOB
- 关于简单自定义view的View的理解(制作上面是图片下面是文字的控件)
- 关于一个App的架构思考
