信号种类	参数取值	时间函数
直流信号	σ=0, ω=0	x(t)=1x(t)=1x(t)=1
实指数信号	σ≠0, ω=0	x(t)=eσtx(t)=e^{σt}x(t)=eσt
虚指数信号	σ=0, ω≠0	x(t)=cos(ωt)+jsin(ωt)x(t)=cos(ωt)+jsin(ωt)x(t)=cos(ωt)+jsin(ωt)
复指数信号	σ≠0, ω≠0	x(t)=eσtcos(ωt)+jeσtsin(ωt)x(t)=e^{σt}cos(ωt)+je^{σt}sin(ωt)x(t)=eσtcos(ωt)+jeσtsin(ωt)

根据上表可知，σ和ω的取值（s的取值）直接决定了复指数信号的种类，在数学上，将σOω坐标面称为s平面，因此有序数对(σ,ω)在s平面中所处的位置决定了复指数信号的类型，具体情况如下：

位置(σ,ω) (σ>0,ω>0)	信号种类
原点(0,0)	直流信号
σ轴正半轴(σ,0)	指数信号(单调递增）
第二象限(-σ,ω)	衰减振荡信号
σ轴负半轴(-σ,0)	指数信号(单调递增）

二、离散时间复指数信号

而在时间离散的情况下，形如

x[n]=zn=(rejΩ)n=rnejΩn（z=rejΩ,−∞<n<+∞）x\left[ n\right] =z^{n}=\left( re^{j\Omega }\right) ^{n}=r^{n}e^{j\Omega n}（z=re^{j\Omega},-\infty <n <+\infty）x[n]=zn=(rejΩ)n=rnejΩn（z=rejΩ,−∞<n<+∞）

的信号，称为离散时间复指数信号或复指数序列，其中r为复数z的模，Ω为幅角

复指数序列中的z与连续复指数信号中的s性质较为类似，s常采用直角坐标系s=σ+jω的方法表示，而z则常使用极坐标的方式进行表示，二者均属于复常数，因此根据r和Ω的取值，复指数序列同样也可以分为多个种类：

信号种类	参数取值	时间函数
实指数序列（单调递增）	Ω=0	x[n]=rnx =r^nx[n]=rn
实指数序列（单调递减）	Ω=π	x[n]=(−r)nx =(-r)^nx[n]=(−r)n
虚指数序列	r=1	x[n]=ejΩn=cos[Ωn]+jsin[Ωn]x =e^{jΩn}=cos[Ωn]+jsin[Ωn]x[n]=ejΩn=cos[Ωn]+jsin[Ωn]
复指数序列		x[n]=rncos[Ωn]+jrnsin[Ωn]x =r^ncos[Ωn]+jr^nsin[Ωn]x[n]=rncos[Ωn]+jrnsin[Ωn]

以复数z的实部Re[z]为横轴，虚部j·Im[z]作为纵轴，建立z平面，可知：
|z|<1（单位圆内），对应指数衰减振荡序列；
|z|=1（单位圆上），对应正弦序列；
|z|>1（单位圆外），对应指数增长振荡序列。

2虚指数序列的实部是正弦序列，其数学表达式为：x[n]=cos⁡[Ω0⋅n+φ]x\left[ n\right] =\cos \left[ \Omega _{0}\cdot n+\varphi \right]x[n]=cos[Ω0⋅n+φ]，时间连续正弦信号可转化为正弦序列：x(t)=cos⁡(ω0⋅t+φ)⟶t=nTx[n]=cos[ω0nT+φ]x\left( t\right) =\cos \left( \omega_{0} \cdot t+\varphi \right)\stackrel{t=nT}{\longrightarrow}x
= cos[ \omega_{0}nT+\varphi]x(t)=cos(ω0⋅t+φ)⟶t=nTx[n]=cos[ω0nT+φ]，此处Ω0与ω0分别为离散时间和连续时间的基本角频率，此处的T为离散时间的采样间隔，通常采样间隔恒定不变。由此可得Ω0与ω0的关系为：

Ω0=ω0T=ω0fs=2πf0fs\Omega _{0}=\omega_{0}T=\dfrac{\omega_{0}}{f_{s}}=2\pi \dfrac{f_{0}}{f_{s}}Ω0=ω0T=fsω0=2πfsf0

其中
ω0——模拟角频率（rad/s）\qquad ω_{0}——模拟角频率（rad/s）ω0——模拟角频率（rad/s）
Ω0——数字域频率（rad）\qquad Ω_{0}——数字域频率（rad）Ω0——数字域频率（rad）
T——采样频率（s）\qquad T——采样频率（s）T——采样频率（s）
f0——模拟频率（Hz）\qquad f_{0}——模拟频率（Hz）f0——模拟频率（Hz）
fs——采样频率（Hz）\qquad f_{s}——采样频率（Hz）fs——采样频率（Hz）

因此，数字域频率Ω是模拟角频率ω对采样频率的归一化。

2.1.2 单位阶跃信号

一、连续时间单位阶跃信号

定义一个连续时间信号，该信号在t=0之前信号的数值均为0，在t=0之后均为1，则称该信号为连续时间单位阶跃信号，其定义的符号表达式如下：

u(t)={1，t>00，t<0u\left( t\right) =\begin{cases}1，t >0\\ 0，t <0\end{cases}u(t)={1，t>00，t<0

将该定义推广，得：

Au(t−t0)={A，t>t00，t<t0Au\left( t-t_{0}\right) =\begin{cases}A，t >t_{0}\\ 0，t <t_{0}\end{cases}Au(t−t0)={A，t>t00，t<t0

在实际应用中，单位阶跃信号常用于表示电源开关的接入状态，也常用于表示其他信号，比如：

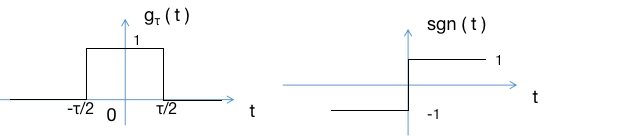
矩形脉冲：指阶跃时间远小于顶部持续时间的平顶脉冲，常用单位阶跃信号进行表示：

gτ(t)=u(t+τ2)−u(t−τ2)g_{\tau }\left( t\right) =u\left( t+\dfrac{\tau }{2}\right) -u\left( t-\dfrac{\tau }{2}\right)gτ(t)=u(t+2τ)−u(t−2τ)

符号函数：当t>0时数值为1，t<0时数值为-1的函数称为符号函数，对任意函数f(t)，都有f(t)=sgn(t)·|f(t)|，其符号表达式表示为：

sgn(t)={1,t>0−1,t<0=u(t)−u(−t)=2⋅u(t)−1sgn\left( t\right) =\begin{cases}1,t >0\\ -1,t <0\end{cases}=u(t)-u(-t)=2·u(t)-1sgn(t)={1,t>0−1,t<0=u(t)−u(−t)=2⋅u(t)−1

二、离散时间单位阶跃信号

与连续时间单位阶跃信号类似，离散时间单位阶跃信号（或称单位阶跃序列）在n=0之前信号的数值均为0，在n=0之后均为1，但是有所不同的是，连续时间单位阶跃信号在t=0上没有定义，而单位阶跃序列在n=0时取常数1，符号表达式为：

u[n]={1，n≥00，n<0u\left[ n\right] =\begin{cases}1，n ≥0\\ 0，n <0\end{cases}u[n]={1，n≥00，n<0

类似的，将单位阶跃序列推广，可得：

Au[n−k]={A，n≥k0，n<kAu\left[ n-k\right] =\begin{cases}A，n ≥ k\\ 0，n <k\end{cases}Au[n−k]={A，n≥k0，n<k

2.1.3 连续时间单位冲激信号

当矩阵脉冲从-τ/2到τ/2的积分为1，宽度τ无限趋近于0，高度1/τ趋近于无穷大时，该信号的作用时间极短，相应物理量极大。数学上称这一类信号为连续时间单位冲激信号，其数学定义为：

δ(t)={δ(t)=0，t≠0∫−∞∞δ(t)dt=1\delta \left( t\right) =\begin{cases}\delta \left( t\right) =0，t\neq 0\\\\ \int _{-\infty }^{\infty }\delta \left( t\right) dt=1\end{cases}δ(t)=⎩⎪⎨⎪⎧δ(t)=0，t=0∫−∞∞δ(t)dt=1

推广为：

Aδ(t)={Aδ(t)=0，t≠0∫−∞∞Aδ(t)dt=AA\delta \left( t\right) =\begin{cases}A\delta \left( t\right) =0，t\neq 0\\\\ \int _{-\infty }^{\infty }A\delta \left( t\right) dt=A\end{cases}Aδ(t)=⎩⎪⎨⎪⎧Aδ(t)=0，t=0∫−∞∞Aδ(t)dt=A

连续时间单位冲激信号主要有以下性质：

筛选性：设x(t)为在t0处连续的普通函数，则有：

x(t)δ(t−t0)=x(t0)δ(t−t0)x(t)\delta \left( t-t_{0}\right)=x(t_{0})\delta \left( t-t_{0}\right)x(t)δ(t−t0)=x(t0)δ(t−t0)

该式表明，通过信号x(t)与冲激函数δ(t-t0)相乘，可筛选出连续时间信号x(t)在t0处的函数值x(t0)，其相乘结果仍为冲激信号，在t0瞬间数值仍趋于无穷大，但冲激强度由 1 变为x(t0)。
取样性：设x(t)为在t0处连续的普通函数，则有：

∫−∞∞x(t)δ(t−t0)dt=x(t0)\int _{-\infty }^{\infty }x(t)\delta \left( t-t_{0}\right) dt=x(t_{0})∫−∞∞x(t)δ(t−t0)dt=x(t0)

该式表明，通过信号x(t)与冲激函数δ(t-t0)相乘，并在时间域 (-∞,+∞) 上积分，可得到x(t)在t0处的取值x(t0)。一个普通函数x(t)与冲激函数δ(t)乘积下的面积等于x(t)在冲激瞬间的值。
展缩性：δ(at+b)=1∣a∣δ(t+ba)\delta \left( at+b\right) =\dfrac{1}{\left| a\right| }\delta \left( t+\dfrac{b}{a}\right)δ(at+b)=∣a∣1δ(t+ab)

证明如下：

∫−∞∞δ(at+b)f(t)dt=τ=at+b1∣a∣∫−∞∞δ(τ)f(τ−ba)dτ=1∣a∣f(−ba)\quad\int _{-\infty }^{\infty }\delta \left( at+b\right) f\left( t\right) dt\xlongequal {\tau = at+b}\dfrac{1}{\left| a\right| }\int _{-\infty }^{\infty }\delta \left( \tau\right) f\left( \dfrac{\tau -b}{a}\right) d\tau =\dfrac{1}{\left| a\right| }f\left( -\dfrac{b}{a}\right)∫−∞∞δ(at+b)f(t)dtτ=at+b∣a∣1∫−∞∞δ(τ)f(aτ−b)dτ=∣a∣1f(−ab)

=∫−∞∞1∣a∣δ(t+ba)f(t)dt=1∣a∣f(−ba)=\int _{-\infty }^{\infty }\dfrac{1}{\left| a\right| }\delta \left( t+\dfrac{b}{a}\right) f\left( t\right) dt=\dfrac{1}{\left| a\right| }f\left( -\dfrac{b}{a}\right)=∫−∞∞∣a∣1δ(t+ab)f(t)dt=∣a∣1f(−ab)

∴δ(at+b)=1∣a∣δ(t+ba)\therefore \delta \left( at+b\right) =\dfrac{1}{\left| a\right| }\delta \left( t+\dfrac{b}{a}\right)∴δ(at+b)=∣a∣1δ(t+ab)

根据这一性质，令a=-1、b=0，可得δ(-t)=δ(t)，因此冲激信号δ(t)是偶函数。

连续时间单位冲激信号可由连续时间单位阶跃信号经微分得到：

δ(t)=ddtu(t)\delta \left( t\right)=\dfrac{d}{dt}u\left( t\right)δ(t)=dtdu(t)

也就是说通过对单位冲激信号积分为可得到单位阶跃信号：

∫−∞tδ(τ)dτ=u(t)\int _{-\infty }^{t}\delta \left( \tau \right) d\tau =u\left( t\right)∫−∞tδ(τ)dτ=u(t)

单位冲激信号的微分称为冲激偶信号，由微分的性质可以得出冲击偶信号属于奇函数，对冲击偶信号进一步求微分可得高阶冲激信号。

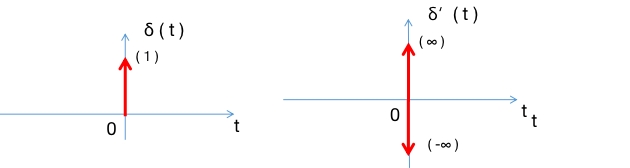
2.1.4 离散时间单位样值信号

定义一个离散时间信号，该信号仅在n=0时数值为1，在n≠0时数值均为0，则称该信号为离散时间单位样值信号，又称为单位样值序列，其定义的符号表达式如下：

δ[n]={1，n=00，n≠0\delta \left[ n\right] =\begin{cases}1，n =0\\ 0，n ≠ 0\end{cases}δ[n]={1，n=00，n=0

将该定义推广，得：

δ[n−k]={1，n=k0，n≠k\delta \left[ n-k\right] =\begin{cases}1，n =k\\ 0，n ≠ k\end{cases}δ[n−k]={1，n=k0，n=k

对于任意一个离散时间信号，都可以使用δ
及δ[n-k]的线性加权和表示

x[n]=∑k=−∞∞x[k]δ[n−k]x\left[ n\right] =\sum ^{\infty }_{k=-\infty }x\left[ k\right] \delta \left[ n-k\right]x[n]=k=−∞∑∞x[k]δ[n−k]

例如下图

可表示为：x
=x[-2]·δ[n+2] + x[-1]·δ[n+1] + x[0]·δ
+ x[1]·δ[n-1] + x[2]·δ[n-2]

对比单位阶跃序列，很容易发现单位样值序列可由单位阶跃序列的差分得到，其符号表达式为

δ[n]=u[n]−u[n−1]δ
=u
-u[n-1]δ[n]=u[n]−u[n−1]

2.2 信号的时域运算

2.2.1 信号的微积分运算

信号的微分：ddtx(t)=x′(t)\dfrac{d}{dt}x\left( t\right) =x'\left( t\right)dtdx(t)=x′(t)

信号的积分：x(−1)(t)=∫−∞tx(τ)dτx^{\left( -1\right) }\left( t\right) =\int _{-\infty }^{t}x\left( \tau \right) d\taux(−1)(t)=∫−∞tx(τ)dτ

2.2.2 信号的展缩、翻转、平移

一、连续时间信号的展缩、翻转、平移

平移： x(t) → x(t+b) b > 0 时，左移；b < 0 时，右移。
翻转： x(t) → x(-t) 波形以纵轴为轴左右翻转。
展缩：（尺度变换） x(t)→x(at)

a>0时，t∈[t1,t2]→t∈[t1a,t2a]\qquad a>0时，t\in \left[ t_{1},t_{2}\right] \rightarrow t\in \left[ \dfrac{t_{1}}{a},\dfrac{t_{2}}{a}\right]a>0时，t∈[t1,t2]→t∈[at1,at2]

若a>1，波形被压缩为原来的1a\\\qquad 若a>1，波形被压缩为原来的\dfrac{1}{a}若a>1，波形被压缩为原来的a1

若a<1，波形被扩展为原来的a倍\\\qquad 若a<1，波形被扩展为原来的a倍若a<1，波形被扩展为原来的a倍

展缩、翻转、平移：可将按照任意顺序进行上述计算，例如：

二、离散时间信号的展缩、翻转、平移

离散时间信号的展缩、翻转、平移： x
→x[an+b]，a、b为实常数，a≠0

离散时间信号波形的翻转和平移的方法与连续信号相同，而展缩变换有所不同，由于离散时间信号时间不连续的特性，导致该类信号在进行压缩时会导致部分信号的丢失；在进行扩展的时候会导致信号在部分时间上没有定义。

2.2.2 信号的分解

信号可以分解成以下几种形式：

信号分解为奇偶信号之和
信号分解为基本信号的有限项之和
信号的因子分解
信号分解为矩阵脉冲之和
信号分解为正交信号分量之和

这里着重介绍信号分解为矩形脉冲之和的方法

由上图，将连续时间信号x(t)分解为多个矩形脉冲之和，这些矩形脉冲的宽度均为τ，则

x(t)≈x(0)⋅g(t)+x(Δτ)⋅g(t−Δτ)+...+x(nΔτ)⋅g(t−nΔτ)x(t)≈x(0)·g(t)+x(Δτ)·g(t-Δτ)+...+x(nΔτ)·g(t-nΔτ)x(t)≈x(0)⋅g(t)+x(Δτ)⋅g(t−Δτ)+...+x(nΔτ)⋅g(t−nΔτ)

=∑k=−∞∞x(nΔτ)⋅g(t−nΔτ)=∑k=−∞∞x(nΔτ)⋅g(t−nΔτ)Δτ⋅Δτ=\sum ^{\infty }_{k=-\infty }x(nΔτ)·g(t-nΔτ)=\sum ^{\infty }_{k=-\infty }x(nΔτ)·\dfrac {g(t-nΔτ)}{Δτ}·Δτ=∑k=−∞∞x(nΔτ)⋅g(t−nΔτ)=∑k=−∞∞x(nΔτ)⋅Δτg(t−nΔτ)⋅Δτ

当Δτ → 0时，n Δ τ → τ ，g(t−nΔτ)Δτ\dfrac {g(t-nΔτ)}{Δτ}Δτg(t−nΔτ) → δ (t-τ )，Δ τ → d τ

x(t)=∫−∞∞x(τ)⋅δ(t−τ)dτx(t)=\int _{-\infty }^{\infty }x(\tau)·\delta \left( t-\tau\right) d\taux(t)=∫−∞∞x(τ)⋅δ(t−τ)dτ

类似地，任意离散时间信号可分解为：
x[n]=∑k=−∞∞x[k]⋅δ[n−k]x
=\sum ^{\infty }_{k=-\infty }x[k]·\delta[n-k]x[n]=k=−∞∑∞x[k]⋅δ[n−k]

2.3 卷积积分、卷积和

2.3.1 卷积的定义

卷积积分：x1(t)∗x2(t)=∫−∞∞x1(τ)x2(t−τ)dτx_{1}(t)*x_{2}(t)=\int _{-\infty }^{\infty}x_{1} \left( \tau \right)x_{2}(t-\tau) d\taux1(t)∗x2(t)=∫−∞∞x1(τ)x2(t−τ)dτ

卷积和：x1[n]∗x2[n]=∑k=−∞∞x1[k]⋅x2[n−k]x_{1}
*x_{2}
=\sum ^{\infty }_{k=-\infty }x_{1}[k]·x_{2}[n-k]x1[n]∗x2[n]=∑k=−∞∞x1[k]⋅x2[n−k]

卷积的物理意义：揭示了LTI系统的零状态响应与输入信号、系统单位冲激响应之间的关系。

2.3.2 卷积的图解法

卷积积分运算：x1(t)∗x2(t)=∫−∞∞x1(τ)x2(t−τ)dτx_{1}(t)*x_{2}(t)=\int _{-\infty }^{\infty}x_{1} \left( \tau \right)x_{2}(t-\tau) d\tau\quadx1(t)∗x2(t)=∫−∞∞x1(τ)x2(t−τ)dτ实际上包含了四个步骤：

换元 t→τ
翻转 x2(τ)→x2(-τ)
移位 x2(-τ)→x2(t-τ)
相乘积分

p1(t)p_{1}(t)p1(t)与p2(t)p_{2}(t)p2(t)的卷积运算 p1(t)∗p2(t)p_{1}(t)*p_{2}(t)p1(t)∗p2(t) 具体图解如下：

可以看出，两个有限长信号卷积，卷积后信号的长度为原两信号长度之和，起始时刻为原信号起始时刻之和。

卷积和运算：x1[n]∗x2[n]=∑k=−∞∞x1[k]⋅x2[n−k]x_{1}
*x_{2}
=\sum ^{\infty }_{k=-\infty }x_{1}[k]·x_{2}[n-k]x1[n]∗x2[n]=∑k=−∞∞x1[k]⋅x2[n−k]同样包含了四个步骤：

换元 n→k
翻转 x2[k]→x2[-k]
移位 x2[-k]→x2[n-k]
相乘求和

x1[n]x_{1}
x1[n]与x2[n]x_{2}
x2[n]的卷积运算 x1[n]∗x2[n]x_{1}
*x_{2}
x1[n]∗x2[n] 具体图解如下：

可以看出，两个有限长序列卷积，卷积后序列的长度为原两序列长度和-1，起始时刻为原序列起始时间之和。

对于卷积和，还可以使用下图所示的竖式法

遵循的规则：

右端对齐
各点分别相乘相加，不进位
起始序号为两序列起始序号之和

2.3.3 卷积的性质

1. 卷积代数

交换律：x1(t)∗x2(t)=x2(t)∗x1(t)x_{1}(t) * x_{2}(t) = x_{2}(t) * x_{1}(t)x1(t)∗x2(t)=x2(t)∗x1(t)
分配律：x1(t)∗[x2(t)+x3(t)]=x1(t)∗x2(t)+x1(t)∗x3(t)x_{1}(t)*[x_{2}(t)+ x_{3}(t)]= x_{1}(t)*x_{2}(t)+ x_{1}(t)*x_{3}(t)x1(t)∗[x2(t)+x3(t)]=x1(t)∗x2(t)+x1(t)∗x3(t)
结合律：[x1(t)∗x2(t)]∗x3(t)=x1(t)∗[x2(t)∗x3(t)][x_{1}(t)*x_{2}(t)]*x_{3}(t) = x_{1}(t)*[x_{2}(t)*x_{3}(t)][x1(t)∗x2(t)]∗x3(t)=x1(t)∗[x2(t)∗x3(t)]

2. 冲激信号的卷积特性

δ(t)∗x(t)=x(t)\delta(t)*x(t)=x(t)δ(t)∗x(t)=x(t)，称δ(t)是卷积积分的单位元。
证明：δ(t)∗x(t)=∫−∞∞δ(τ)x(t−τ)dτ=x(t)\delta(t)*x(t)=\int_{-\infty}^{\infty}\delta(\tau)x(t-\tau)d\tau=x(t)δ(t)∗x(t)=∫−∞∞δ(τ)x(t−τ)dτ=x(t)
δ(t−t0)∗x(t)=x(t−t0)\delta(t-t_{0})*x(t)=x(t-t_{0})δ(t−t0)∗x(t)=x(t−t0)，称δ(t−t0)\delta(t-t_{0})δ(t−t0)为延时器。
推论：如果x1(t)∗x2(t)=y(t)x_{1}(t)*x_{2}(t)=y(t)x1(t)∗x2(t)=y(t)，那么x1(t)∗x2(t−t0)=y(t−t0)x_{1}(t)*x_{2}(t-t_{0})=y(t-t_{0})x1(t)∗x2(t−t0)=y(t−t0)
x1(t−t1)∗x2(t−t2)=y(t−t1−t2)\qquad \qquad \qquad x_{1}(t-t_{1})*x_{2}(t-t_{2})=y(t-t_{1}-t_{2})x1(t−t1)∗x2(t−t2)=y(t−t1−t2)
该性质称为卷积的时不变性，该性质对于离散样值信号同样有效：
δ[n]∗x[n]=x[n]δ[n−n0]∗x[n]=x[n−n0]\delta
*x
=x
\quad \delta[n-n_{0}]*x
=x[n-n_{0}]δ[n]∗x[n]=x[n]δ[n−n0]∗x[n]=x[n−n0]

3.卷积的微分特性

δ′(t)∗x(t)=x′(t)\delta'(t)*x(t)=x'(t)δ′(t)∗x(t)=x′(t)，称δ’(t)是微分器。
推论：δ(n)(t)∗x(t)=x(n)(t)\delta^{(n)}(t)*x(t)=x^{(n)}(t)δ(n)(t)∗x(t)=x(n)(t)

dx1(t)dt∗x2(t)=x1(t)∗dx2(t)dt=ddt[x1(t)∗x2(t)]\qquad\dfrac{dx_{1}(t)}{dt}*x_{2}(t)=x_{1}(t)*\dfrac{dx_{2}(t)}{dt}=\dfrac{d}{dt}[x_{1}(t)*x_{2}(t)]dtdx1(t)∗x2(t)=x1(t)∗dtdx2(t)=dtd[x1(t)∗x2(t)]

4.卷积的积分特性

x(t)∗u(t)=∫−∞tx(τ)dτx(t)*u(t)=\int_{-\infty}^{t}x(\tau)d\taux(t)∗u(t)=∫−∞tx(τ)dτ，称u(t)是模拟积分器。

证明：x(t)∗u(t)=∫−∞∞x(τ)u(t−τ)dτ=∫−∞tx(τ)dτx(t)*u(t)=\int_{-\infty}^{\infty}x(\tau)u(t-\tau)d\tau=\int_{-\infty}^{t}x(\tau)d\taux(t)∗u(t)=∫−∞∞x(τ)u(t−τ)dτ=∫−∞tx(τ)dτ

推论：[∫−∞tx1(τ)dτ]∗x2(t)\left[ \int _{-\infty }^{t}x_{1}\left( \tau \right) d\tau \right] \ast x_{2}\left( t\right)[∫−∞tx1(τ)dτ]∗x2(t)

=x1(t)∗[∫−∞tx2(τ)dτ]\qquad\qquad=x_{1}\left( t\right) \ast \left[ \int _{-\infty }^{t}x_{2}\left( \tau \right) d\tau \right]=x1(t)∗[∫−∞tx2(τ)dτ]

=∫−∞t[x1(τ)∗x2(τ)dτ]\qquad\qquad=\int _{-\infty }^{t}\left[ x_{1}\left( \tau\right) \ast x_{2}\left( \tau\right) d\tau\right]=∫−∞t[x1(τ)∗x2(τ)dτ]

x1(t)∗x2(t)=∫−∞tx1(τ)dτ∗dx2(t)dt=dx1(t)dt∗∫−∞tx2(τ)dτ\qquad x_{1}(t)*x_{2}(t)=\int_{-\infty}^{t}x_{1}(\tau)d\tau*\dfrac{dx_{2}(t)}{dt}=\dfrac{dx_{1}(t)}{dt}*\int_{-\infty}^{t}x_{2}(\tau)d\taux1(t)∗x2(t)=∫−∞tx1(τ)dτ∗dtdx2(t)=dtdx1(t)∗∫−∞tx2(τ)dτ

上式成立条件：lim⁡t→−∞x1(t)=lim⁡t→−∞x2(t)=0\lim _{t\rightarrow -\infty }x_{1}\left( t\right) =\lim _{t\rightarrow -\infty }x_{2}\left( t\right) =0t→−∞limx1(t)=t→−∞limx2(t)=0

5.卷积的求和特性

x[n]∗u[n]=∑k=−∞nx[k]x
*u
=\sum_{k=-\infty}^{n}x[k]x[n]∗u[n]=∑k=−∞nx[k]，称u
是数字积分器。

推论：[∑k=−∞nx1[k]]∗x2[n]=x1[n]∗[∑k=−∞nx2[k]]=∑k=−∞n[x1[k]∗x2[k]]\left[ \sum ^{n}_{k=-\infty }x_{1}\left[ k\right] \right] \ast x_{2}\left[ n\right]=x_{1}\left[ n\right] \ast \left[ \sum ^{n}_{k=-\infty }x_{2}\left[ k\right] \right]=\sum ^{n}_{k=-\infty }\left[ x_{1}\left[ k\right] \ast x_{2}\left[ k\right] \right][∑k=−∞nx1[k]]∗x2[n]=x1[n]∗[∑k=−∞nx2[k]]=∑k=−∞n[x1[k]∗x2[k]]

2.4 连续时间系统的时域分析

2.4.1 连续时间系统的数学模型——微分方程

1. 微分方程的基本形式：

dndtny(t)+an−1dn−1dtn−1y(t)+…+a1ddty(t)+a0y(t)=bmdmdtmx(t)+…+b1ddtx(t)+b0x(t)\dfrac{d^{n}}{dt^{n}}y\left( t\right) +a_{n-1}\dfrac{d^{n-1}}{dt^{n-1}}y\left( t\right) +\ldots +a_{1}\dfrac{d}{dt}y\left( t\right) +a_{0}y\left( t\right)=b_{m}\dfrac{d^{m}}{dt^{m}}x\left( t\right) +\ldots +b_{1}\dfrac{d}{dt}x\left( t\right) +b_{0}x\left( t\right)dtndny(t)+an−1dtn−1dn−1y(t)+…+a1dtdy(t)+a0y(t)=bmdtmdmx(t)+…+b1dtdx(t)+b0x(t)

2. 微分方程的求解方法

时域解法
微分方程的解分为齐次解yn(t)和特解yf(t)。y(t)=yn(t)+yf(t)
零输入/零状态解法
全响应=零输入响应yzi(t)+零状态响应yzs(t)。y(t)=yzi(t)+yzs(t)
变换域解法
通过拉普拉斯变换求解微分方程。

此处重点讨论零输入/零响应解法

全响应=零输入响应yzi(t)+零状态响应yzs(t)。y(t)=yzi(t)+yzs(t)
零输入响应：输入x(t)为零，仅由初始状态产生的响应，记为yzi(t)
零状态响应：初始状态为零，仅由输入信号x(t)产生的响应，记为yzs(t)

通常取t=0时刻作为起始时刻
输入信号在t=0时刻之后作用于系统，记为x(t)=f(t)·u(t)
t=0−t=0^{-}t=0−时刻系统的状态称为t=0−t=0^{-}t=0−状态，记为y(0−)y(0^{-})y(0−)、y′(0−)y'(0^{-})y′(0−)…
t=0+t=0^{+}t=0+时刻系统的状态称为t=0+t=0^{+}t=0+状态，记为y(0+)y(0^{+})y(0+)、y′(0+)y'(0^{+})y′(0+)…

零输入响应由于其输入为0，根据微分方程齐次方程求解：

dndtny(t)+an−1dn−1dtn−1y(t)+…+a1ddty(t)+a0y(t)=0\dfrac{d^{n}}{dt^{n}}y\left( t\right) +a_{n-1}\dfrac{d^{n-1}}{dt^{n-1}}y\left( t\right) +\ldots +a_{1}\dfrac{d}{dt}y\left( t\right) +a_{0}y\left( t\right)=0dtndny(t)+an−1dtn−1dn−1y(t)+…+a1dtdy(t)+a0y(t)=0

其特征方程为：D(λ)=λn+an−1λn−1+...+a1λ+a0=0D(\lambda)=\lambda^{n}+a_{n-1}\lambda^{n-1}+...+a_{1}\lambda+a_{0}=0D(λ)=λn+an−1λn−1+...+a1λ+a0=0
通过因式分解，解得特征根 λ1,λ2,...,λnλ_{1} , λ_{2} , ... , λ_{n}λ1,λ2,...,λn

特征根为单实根时，可得微分方程的齐次通解：yzi(t)=c1eλ1t+c2eλ2t+...+cneλnty_{zi}(t)=c_{1}e^{\lambda_{1}t}+c_{2}e^{\lambda_{2}t}+...+c_{n}e^{\lambda_{n}t}yzi(t)=c1eλ1t+c2eλ2t+...+cneλnt

其中，eλte^{\lambda t}eλt称为特征模式，这也是连续时间指数信号一般表示成este^{st}est的形式的原因。
零输入响应时齐次方程的解，其形式与时域解法中的齐次通解相同。
待定系数由初始状态yzi(0−)=y(0−)、yzi′(0−)=y′(0−)y_{zi}(0^{-})=y(0^{-})、y_{zi}'(0^{-})=y'(0^{-})yzi(0−)=y(0−)、yzi′(0−)=y′(0−)确定。

例1：RLC电路如图所示，i(t)为输出，R=3Ω，L=1H，C=12F，例1：RLC电路如图所示，i(t)为输出，R=3\Omega，L=1H，C=\dfrac{1}{2}F，例1：RLC电路如图所示，i(t)为输出，R=3Ω，L=1H，C=21F，

输入x(t)=10e−3tu(t)，i(0−)=0，uc(0−)=5V，试求其零输入响应izi(t)输入x(t)=10e^{-3t}u(t)，i(0^{-})=0，u_{c}(0^{-})=5V，试求其零输入响应i_{zi}(t)输入x(t)=10e−3tu(t)，i(0−)=0，uc(0−)=5V，试求其零输入响应izi(t)

根据电感、电阻、电容与电流的关系，建立将该电路的模型为：

Li′′(t)+Ri′(t)+1Ci(t)=x′(t)Li''(t)+Ri'(t)+\dfrac{1}{C}i(t)=x'(t)Li′′(t)+Ri′(t)+C1i(t)=x′(t)

代入参数得：

i′′(t)+3i′(t)+2i(t)=x′(t)i''(t)+3i'(t)+2i(t)=x'(t)i′′(t)+3i′(t)+2i(t)=x′(t)

由此可得微分方程的特征方程为：

λ2+3λ+2=0\lambda^2+3\lambda+2=0λ2+3λ+2=0

因式分解得：

(λ+1)(λ+2)=0(\lambda+1)(\lambda+2)=0(λ+1)(λ+2)=0

由此可得特征根为：

λ1=−1，λ2=−2\lambda_{1}=-1，\lambda_{2}=-2λ1=−1，λ2=−2

将特征根代入可得通解为：

izi(t)=C1e−t+C2e−2t，t>0i_{zi}(t)=C_{1}e^{-t}+C_{2}e^{-2t}，t>0izi(t)=C1e−t+C2e−2t，t>0

该式中仍有C1、C2C_{1}、C_{2}C1、C2两个未知量，通过待定系数法解出：

由基尔霍夫电压定律（KVL）得：

Li′(0−)+Ri(0−)+uc(0−)=0Li'(0^-)+Ri(0^-)+u_c(0^-)=0 Li′(0−)+Ri(0−)+uc(0−)=0

解得：

i′(0−)=−5i'(0^-)=-5i′(0−)=−5

对izi(t)=C1e−t+C2e−2i_{zi}(t)=C_{1}e^{-t}+C_{2}e^{-2}izi(t)=C1e−t+C2e−2求导，得：

i′(t)=−C1e−t−2C2e−2ti'(t)=-C_1e^{-t}-2C_2e^{-2t}i′(t)=−C1e−t−2C2e−2t

将i(0−)=0，uc(0−)=5Vi(0^{-})=0，u_{c}(0^{-})=5Vi(0−)=0，uc(0−)=5V代入通解，得：

{i(0)=C1+C2=0i′(0)=−C1−2C2=−5\begin{cases}i\left( 0\right) =C_{1}+C_{2}=0\\ i'\left( 0\right) =-C_{1}-2C_{2}=-5\end{cases}{i(0)=C1+C2=0i′(0)=−C1−2C2=−5

解得：

{C1=−5C2=5\begin{cases}C_{1}=-5\\ C_{2}=5\end{cases}{C1=−5C2=5

从而该RLC电路系统的零输入响应为：

izi(t)=−5e−t+5e−2t，t>0i_{zi}(t)=-5e^{-t}+5e^{-2t}，t>0izi(t)=−5e−t+5e−2t，t>0

3. 单位冲激响应

系统初始状态为零，输入为单位冲激信号δ(t)\delta(t)δ(t)时的响应，称为单位冲激响应，记为h(t)，将h(t)代入微分方程

可得适用于单位冲激响应的微分方程：

h(n)(t)+an−1h(n−1)(t)+...+a0h(t)=bmδ(m)(t)+...+b1δ′(t)+b0δ(t)h^{(n)}(t)+a_{n-1}h^{(n-1)}(t)+...+a_{0}h(t)=b_{m}\delta^{(m)}(t)+...+b_{1}\delta'(t)+b_{0}\delta(t)h(n)(t)+an−1h(n−1)(t)+...+a0h(t)=bmδ(m)(t)+...+b1δ′(t)+b0δ(t)

由于该方程右侧由高阶冲激信号构成，只在t=0处不为零，在其他位置均为零，因此可以通过求齐次通解的方法来求解h(t)中t≠0的部分，其通解表示为特征模式项之和：

y(t)=c1eλ1t+c2eλ2t+...+cneλnty(t)=c_{1}e^{\lambda_{1}t}+c_{2}e^{\lambda_{2}t}+...+c_{n}e^{\lambda_{n}t}y(t)=c1eλ1t+c2eλ2t+...+cneλnt

将通解与单位阶跃信号相乘，表示t>0时的情况

当t=0时，需要考虑高阶冲激信号产生的响应，该响应取决于单位冲激响应微分方程中的最高阶数m和n的大小：

当n>m时，h(t)=h(t)=h(t)=[特征模式项之和]u(t)u(t)u(t)
当n=m时，h(t)=bm+h(t)=b_{m}+h(t)=bm+[特征模式项之和]u(t)u(t)u(t)
当n<m时，h(t)h(t)h(t)会产生高阶冲激信号

例2：已知某LTI系统y′′(t)+3y′(t)+2y(t)=x′(t)，试求其单位冲激响应h(t)例2：已知某LTI系统y''(t)+3y'(t)+2y(t)=x'(t)，试求其单位冲激响应h(t)例2：已知某LTI系统y′′(t)+3y′(t)+2y(t)=x′(t)，试求其单位冲激响应h(t)

根据

y′′(t)+3y′(t)+2y(t)=x′(t)y''(t)+3y'(t)+2y(t)=x'(t)y′′(t)+3y′(t)+2y(t)=x′(t)

代入δ(t)\delta(t)δ(t)可得：

h′′(t)+3h′(t)+2h(t)=δ′(t)h''(t)+3h'(t)+2h(t)=\delta'(t)h′′(t)+3h′(t)+2h(t)=δ′(t)

可得特征方程：

λ2+3λ+2=0\lambda^2+3\lambda+2=0λ2+3λ+2=0

解得特征根：

λ1=−1，λ2=−2\lambda_{1}=-1，\lambda_{2}=-2λ1=−1，λ2=−2

由此可得单位冲激响应：

h(t)=(C1e−t+C2e−2t)u(t)h(t)=(C_1e^{-t}+C_2e^{-2t})u(t)h(t)=(C1e−t+C2e−2t)u(t)

h′(t)=(C1e−t+C2e−2t)δ(t)+(−C1e−t−2C2e−2t)u(t)=(C1+C2)δ(t)+(−C1e−t−2C2e−2t)u(t)\begin{aligned} h'(t) &=(C_1e^{-t}+C_2e^{-2t})\delta(t)+(-C_1e^{-t}-2C_2e^{-2t})u(t)\\&=(C_1+C_2)\delta(t)+(-C_1e^{-t}-2C_2e^{-2t})u(t)\end{aligned}h′(t)=(C1e−t+C2e−2t)δ(t)+(−C1e−t−2C2e−2t)u(t)=(C1+C2)δ(t)+(−C1e−t−2C2e−2t)u(t)

h′′(t)=(C1+C2)δ′(t)+(−C1−2C2)δ(t)+(C1e−t+4C2e−2t)u(t)h''(t)=(C_1+C_2)\delta'(t)+(-C_1-2C_2)\delta(t)+(C_1e^{-t}+4C_2e^{-2t})u(t)h′′(t)=(C1+C2)δ′(t)+(−C1−2C2)δ(t)+(C1e−t+4C2e−2t)u(t)

通过冲激平衡法，将h′′(t)、h′(t)、h(t)h''(t)、h'(t)、h(t)h′′(t)、h′(t)、h(t)代入h′′(t)+3h′(t)+2h(t)=δ′(t)h''(t)+3h'(t)+2h(t)=\delta'(t)h′′(t)+3h′(t)+2h(t)=δ′(t)，解得：

C1=−1，C2=2C_1=-1，C_2=2C1=−1，C2=2

由此可得单位冲激响应：

h(t)=(−e−t+2e−2t)u(t)h(t)=(-e^{-t}+2e^{-2t})u(t)h(t)=(−e−t+2e−2t)u(t)

4. 零状态响应

因为系统单位冲激响应为

δ(t)→h(t)\delta(t)\rightarrow h(t)δ(t)→h(t)

根据时不变性：

δ(t−nΔτ)→h(t−nΔτ)\delta(t-n\Delta\tau) \rightarrow h(t-n\Delta\tau)δ(t−nΔτ)→h(t−nΔτ)

根据齐次性：

x(nΔτ)δ(t−nΔτ)Δτ→x(nΔτ)h(t−nΔτ)Δτx(n\Delta\tau)\delta(t-n\Delta\tau)\Delta\tau\rightarrow x(n\Delta\tau)h(t-n\Delta\tau)\Delta\taux(nΔτ)δ(t−nΔτ)Δτ→x(nΔτ)h(t−nΔτ)Δτ

根据可加性：

∑n=−∞∞x(nΔτ)δ(t−nΔτ)Δτ→∑n=−∞∞x(nΔτ)h(t−nΔτ)Δτ\sum_{n=-\infty}^{\infty}x(n\Delta\tau)\delta(t-n\Delta\tau)\Delta\tau\rightarrow\sum_{n=-\infty}^{\infty}x(n\Delta\tau)h(t-n\Delta\tau)\Delta\taun=−∞∑∞x(nΔτ)δ(t−nΔτ)Δτ→n=−∞∑∞x(nΔτ)h(t−nΔτ)Δτ

当Δτ→0\Delta\tau\rightarrow0Δτ→0时，可以得出：

x(t)=∫−∞∞x(τ)δ(t−τ)dτ→yzs(t)=∫−∞∞x(τ)h(t−τ)dτx(t)=\int_{-\infty}^{\infty}x(\tau)\delta(t-\tau)d\tau \rightarrow y_{zs}(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\taux(t)=∫−∞∞x(τ)δ(t−τ)dτ→yzs(t)=∫−∞∞x(τ)h(t−τ)dτ

首先分析x(t)x(t)x(t)和δ(t)\delta(t)δ(t)的关系：

x(t)=∫−∞∞x(τ)δ(t−τ)dτ=x(t)∗δ(t)\begin{aligned} x(t) &=\int_{-\infty}^{\infty}x(\tau)\delta(t-\tau)d\tau\\&=x(t) * \delta(t)\end{aligned}x(t)=∫−∞∞x(τ)δ(t−τ)dτ=x(t)∗δ(t)

称为“信号的分解特性”。以δ(t)\delta(t)δ(t)为基本信号，将任意的信号x(t)x(t)x(t)分解为δ(t)\delta(t)δ(t)的线性加权组合。

而yzs(t)y_{zs}(t)yzs(t)和h(t)h(t)h(t)的关系：

yzs(t)=∫−∞∞x(τ)h(t−τ)dτy_{zs}(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tauyzs(t)=∫−∞∞x(τ)h(t−τ)dτ

称为“响应的分解特性”，以h(t)h(t)h(t)为基本响应，将x(t)x(t)x(t)产生的yzs(t)y_{zs}(t)yzs(t)分解为h(t)h(t)h(t)的线性加权组合，因此：

零状态响应=输入信号∗单位冲激响应零状态响应=输入信号*单位冲激响应零状态响应=输入信号∗单位冲激响应

5.响应模式分析

例2：RLC电路如图所示，i(t)为输出，R=3Ω，L=1H，C=12F，例2：RLC电路如图所示，i(t)为输出，R=3\Omega，L=1H，C=\dfrac{1}{2}F，例2：RLC电路如图所示，i(t)为输出，R=3Ω，L=1H，C=21F，

输入x(t)=10e−3tu(t)，i(0−)=0，uc(0−)=5V，试求其全输入响应i(t)输入x(t)=10e^{-3t}u(t)，i(0^{-})=0，u_{c}(0^{-})=5V，试求其全输入响应i(t)输入x(t)=10e−3tu(t)，i(0−)=0，uc(0−)=5V，试求其全输入响应i(t)

由例1：

i′′(t)+3i′(t)+2i(t)=x′(t)i''(t)+3i'(t)+2i(t)=x'(t)i′′(t)+3i′(t)+2i(t)=x′(t)

λ2+3λ+2=0\lambda^2+3\lambda+2=0λ2+3λ+2=0

λ1=−1，λ2=−2\lambda_1=-1，\lambda_2=-2λ1=−1，λ2=−2

零输入响应：

izi(t)=−5e−t+5e−2ti_{zi}(t)=-5e^{-t}+5e^{-2t}izi(t)=−5e−t+5e−2t

单位冲激响应：

h(t)=(−e−t+2e−2t)u(t)h(t)=(-e^{-t}+2e^{-2t})u(t)h(t)=(−e−t+2e−2t)u(t)

零状态响应：

izs(t)=x(t)∗h(t)=(−5e−t+20e−2t−15e−3t)u(t)\begin{aligned} i_{zs}(t)&=x(t)*h(t)\\ &=(-5e^{-t}+20e^{-2t}-15e^{-3t})u(t) \end{aligned}izs(t)=x(t)∗h(t)=(−5e−t+20e−2t−15e−3t)u(t)

将零状态响应与零输入响应相加，得全响应：

i(t)=izi(t)+izs(t)=(−5e−t+5e−2t)u(t)+(−5e−t+20e−2t−15e−3t)u(t)\begin{aligned} i(t)&=i_{zi}(t)+i_{zs}(t)\\&=(-5e^{-t}+5e^{-2t})u(t)+(-5e^{-t}+20e^{-2t}-15e^{-3t})u(t) \end{aligned}i(t)=izi(t)+izs(t)=(−5e−t+5e−2t)u(t)+(−5e−t+20e−2t−15e−3t)u(t)

整理可得：

i(t)=(−10e−t+25e−2t−15e−3t)u(t)i(t)=(-10e^{-t}+25e^{-2t}-15e^{-3t})u(t)i(t)=(−10e−t+25e−2t−15e−3t)u(t)

其中，−10e−t+25e−2t-10e^{-t}+25e^{-2t}−10e−t+25e−2t被称为自然响应，也称为自由响应或固有响应，自然响应是由系统特征模式决定的那部分响应，记作yn(t)y_n(t)yn(t)；
而−15e−3t-15e^{-3t}−15e−3t则被称为强迫响应,强迫响应是由激励信号决定的响应，记作yf(t)y_f(t)yf(t)。

整理上述全响应、零输入响应、零状态响应、自然响应和强迫响应的关系可得：

全响应=零输入响应+零状态响应全响应=自然响应+强迫响应自然响应=零输入响应+零状态响应中由系统特征根决定的部分强迫响应=零状态响应中由输入信号特征模式决定的部分零输入响应≠自然响应=一部分自然响应=微分方程的齐次解零状态响应≠强迫响应=另一部分自然响应+强迫响应=微分方程的特解\begin{aligned} 全响应&=零输入响应+零状态响应\\ 全响应&=自然响应+强迫响应\\\\ 自然响应&=零输入响应+零状态响应中由系统特征根决定的部分\\ 强迫响应&=零状态响应中由输入信号特征模式决定的部分\\\\ 零输入响应&≠自然响应=一部分自然响应=微分方程的齐次解\\ 零状态响应&≠强迫响应=另一部分自然响应+强迫响应=微分方程的特解 \end{aligned}全响应全响应自然响应强迫响应零输入响应零状态响应=零输入响应+零状态响应=自然响应+强迫响应=零输入响应+零状态响应中由系统特征根决定的部分=零状态响应中由输入信号特征模式决定的部分=自然响应=一部分自然响应=微分方程的齐次解=强迫响应=另一部分自然响应+强迫响应=微分方程的特解

另外，全响应还可以分解为瞬态响应与稳态响应，瞬态响应指的是系统响应中随着时间的增加而衰减，并且最终完全消失的分量；而那些对着时间的增加一直保留的分量称为稳态响应。

6. 系统的稳定性和因果性分析

如果系统对任何一个有界输入，输出也有界，则称该系统为有界输出稳定系统（BIBO稳定系统），简称稳定系统。
即∣x(t)∣<A|x(t)|<A∣x(t)∣<A，则∣y(t)∣<B|y(t)|<B∣y(t)∣<B

点赞 2
收藏
分享
文章举报

孟德尔的小豆芽发布了3 篇原创文章 · 获赞 4 · 访问量 205 私信关注

内容来自用户分享和网络整理，不保证内容的准确性，如有侵权内容，可联系管理员处理

标签：

相关文章推荐

新的分享

章节导航

《信号与系统》第二章 常用信号及LTI系统的时域分析

第二章 常用信号及LTI系统的时域分析

2.1 常用信号及其基本特性

2.1.1 复指数信号

一、连续时间复指数信号