SVD & Eigen Decomposition

SVD - singular value decomposition

We usually talk about SVD in terms of matrices, A=UΣVTA=UΣVT but we can also think about it in terms of vectors. SVD gives us sets of orthonormal vectors vjvj and ujuj such that

Avj=σjujAvj=σjuj

σjσj are scalars, called singular values.

两边同时右乘 VV，因为 VV 是orthonormal，所以 VT=V−1VT=V−1： AV=UΣAV=UΣ

Does this remind you of anything?

有点像 Av=λvAv=λv ，SVD可以看成是generalization of eigen decomposition。不是所有矩阵都有特征值，但他们都有奇异值。

Q：奇异值和特征值的区别？

先，矩阵可以认为是一种线性变换，而且这种线性变换的作用效果与基的选择有关。以 Ax=bAx=b 为例， xx 是 mm 维向量，bb 是 nn 维向量，m,nm,n 可以相等也可以不相等，表示矩阵可以将一个向量线性变换到另一个向量，这样一个线性变换的作用可以包含旋转、缩放和投影三种类型的效应。

奇异值分解正是对线性变换这三种效应的一个析构。A=μΣσTA=μΣσT，μμ 和 σσ 是两组正交单位向量，ΣΣ 是对角阵，表示奇异值，它表示我们找到了μμ 和 σσ 这样两组基，AA 矩阵的作用是将一个向量从 σσ 这组正交基向量的空间旋转到 μμ 这组正交基向量空间，并对每个方向进行了一定的缩放，缩放因子就是各个奇异值。如果 σσ 维度比 μμ 大，则表示还进行了投影。可以说奇异值分解将一个矩阵原本混合在一起的三种作用效果，分解出来了。

特征值分解其实是对旋转缩放两种效应的归并。（有投影效应的矩阵不是方阵，没有特征值）特征值，特征向量由 Ax=λxAx=λx 得到，它表示如果一个向量 vv 处于 AA 的特征向量方向，那么 AvAv 对 vv 的线性变换作用只是一个缩放。也就是说，求特征向量和特征值的过程，我们找到了这样一组基，在这组基下，矩阵的作用效果仅仅是存粹的缩放。对于实对称矩阵，特征向量正交，我们可以将特征向量式子写成 A=xλxTA=xλxT ，这样就和奇异值分解类似了，就是A矩阵将一个向量从 xx 这组基的空间旋转到 xx 这组基的空间，并在每个方向进行了缩放，由于前后都是 xx ，就是没有旋转或者理解为旋转了0度。

总结一下，特征值分解和奇异值分解都是给一个矩阵(线性变换)找一组特殊的基，特征值分解找到了特征向量这组基，在这组基下该线性变换只有缩放效果。而奇异值分解则是找到另一组基，这组基下线性变换的旋转、缩放、投影三种功能独立地展示出来了。我感觉特征值分解其实是一种找特殊角度，让旋转效果不显露出来，所以并不是所有矩阵都能找到这样巧妙的角度。仅有缩放效果，表示、计算的时候都更方便，这样的基很多时候不再正交了，又限制了一些应用。

Source: https://www.zhihu.com/question/19666954/answer/54788626)

Eigen Decomposition

The best classical methods for computing the SVD are variants on methods for computing eigenvalues. In addition to their links to SVD, Eigen decompositions are useful on their own as well. Here are a few practical applications of eigen decomposition:

Power Method

An n×nn×n matrix AA is diagonalizable if it has nn linearly independent eigenvectors v1,…vnv1,…vn. 翻译成大白话就是eigenvector组成了 AA 的space的基。所以：

Any ww can be expressed w=∑nj=1cjvjw=∑j=1ncjvj, for some scalars cjcj.

即any vector都可以表示为eigenvector的linear combination。这个性质贼有用，因为 Aw=λwAw=λw ，所以我们要对 ww 做 kk 次缩放 AkAk 的话，只需要乘上 kk 次 λλ 即可。

Exercise: Show that Akw=∑j=1ncjλkjvjAkw=∑j=1ncjλjkvj

Question: How will this behave for large kk?

This is inspiration for the power method.

rapid matrix powers

Av=λvAv=λv ，v是eigenvector，写成矩阵的形式就是(注意 ΛΛ 和 VV 的顺序)：

AV=VΛAV=VΛ => A=VΛV−1A=VΛV−1



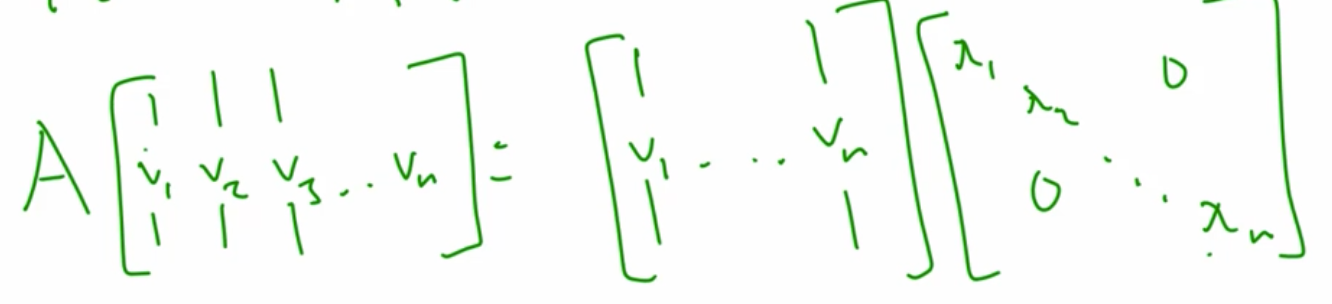
Ak=(VΛV−1)k=VΛkV−1Ak=(VΛV−1)k=VΛkV−1

nth Fibonacci number

The object is to come up with a closed form solution for the nth term of the Fibonacci sequence f={0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …} (I start with zero for the zeroth fibonacci number, and one for the first, but you’ll see that this method allows you to easily compute a Fibonacci-like sequence with any two initial values)

ow lets write an iterative formula for the nth and (n+1)th term, and then we’ll solve for a closed form solution.



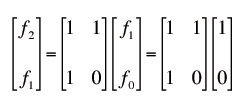
o you can see, by multiplying this matrix repeatedly, it yields the nth and (n+1)th term



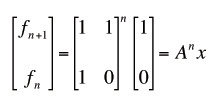
ow to simplify that nasty nth power of A, we’ll use a trick known as diagonalization. If we can write A as a product of 3 matrices P, D and P inverse, where D is a diagonal matrix, it gives us an easy way to write the nth power of A



Behavior of ODEs

Markov Chains (health care economics, Page Rank)

Linear Discriminant Analysis on Iris dataset