Kruskal（克鲁斯卡尔） 最小生成树 算法详解+模板

最小生成树

在含有n个顶点的连通图中选择n-1条边，构成一棵极小连通子图，并使该连通子图中n-1条边上权值之和达到最小，则称其为连通网的最小生成树。



例如，对于如上图G4所示的连通网可以有多棵权值总和不相同的生成树。



克鲁斯卡尔算法介绍

克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法。

基本思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。

具体做法：首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。

克鲁斯卡尔算法图解

以上图G4为例，来对克鲁斯卡尔进行演示(假设，用数组R保存最小生成树结果)。



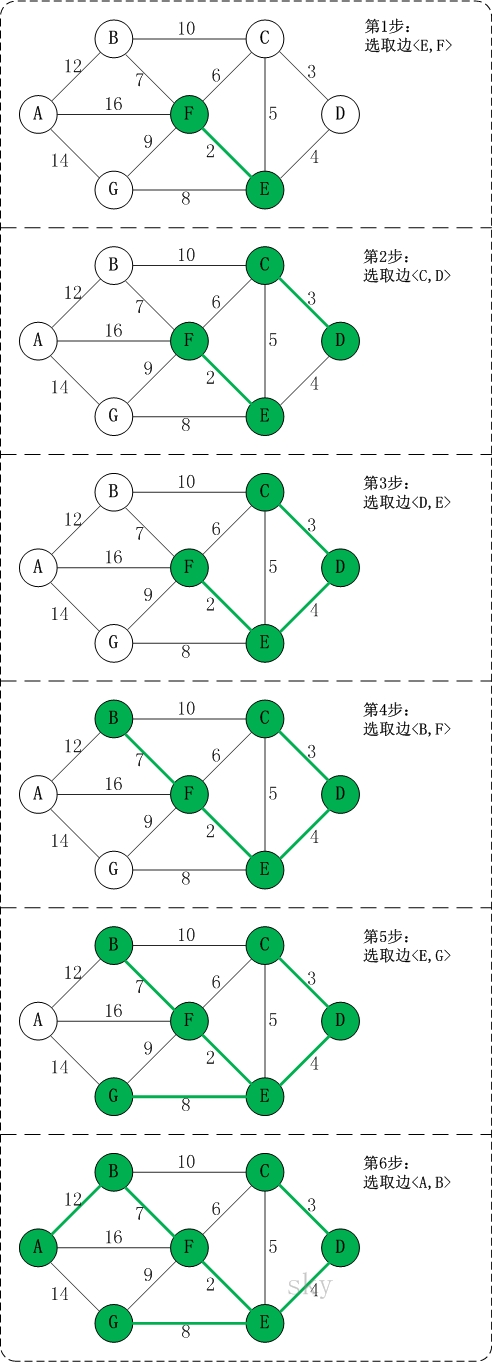
第1步：将边(E,F)加入R中。

边(E,F)的权值最小，因此将它加入到最小生成树结果R中。

第2步：将边(C,D)加入R中。

上一步操作之后，边(C,D)的权值最小，因此将它加入到最小生成树结果R中。

第3步：将边(D,E)加入R中。

上一步操作之后，边(D,E)的权值最小，因此将它加入到最小生成树结果R中。

第四步：将边(B,F)加入R中。

上一步操作之后，边(C,E)的权值最小，但(C,E)会和已有的边构成回路；因此，跳过边(C,E)。同理，跳过边(C,F)。将边(B,F)加入到最小生成树结果R中。

第5步：将边(E,G)加入R中。

上一步操作之后，边(E,G)的权值最小，因此将它加入到最小生成树结果R中。

第6步：将边(A,B)加入R中。

上一步操作之后，边(F,G)的权值最小，但(F,G)会和已有的边构成回路；因此，跳过边(F,G)。同理，跳过边(B,C)。将边(A,B)加入到最小生成树结果R中。

此时，最小生成树构造完成！它包括的边依次是：(E,F) (C,D) (D,E) (B,F) (E,G) (A,B)。

克鲁斯卡尔算法分析

根据前面介绍的克鲁斯卡尔算法的基本思想和做法，我们能够了解到，克鲁斯卡尔算法重点需要解决的以下两个问题：

问题一 对图的所有边按照权值大小进行排序。

问题二 将边添加到最小生成树中时，怎么样判断是否形成了回路。

问题一很好解决，采用排序算法进行排序即可。

问题二，处理方式是：记录顶点在”最小生成树”中的终点，顶点的终点是”在最小生成树中与它连通的最大顶点”(关于这一点，后面会通过图片给出说明)。然后每次需要将一条边添加到最小生存树时，判断该边的两个顶点的终点是否重合，重合的话则会构成回路。 以下图来进行说明：



在将(E,F) (C,D) (D,E)加入到最小生成树R中之后，这几条边的顶点就都有了终点：

**(01) C的终点是F。

(02) D的终点是F。

(03) E的终点是F。

(04) F的终点是F。**

关于终点，就是将所有顶点按照从小到大的顺序排列好之后；某个顶点的终点就是”与它连通的最大顶点”。 因此，接下来，虽然(C,E)是权值最小的边。但是C和E的重点都是F，即它们的终点相同，因此，将(C,E)加入最小生成树的话，会形成回路。这就是判断回路的方式。

克鲁斯卡尔算法的代码说明

有了前面的算法分析之后，下面我们来查看具体代码。这里选取”邻接矩阵”进行说明，对于”邻接表”实现的图在后面的源码中会给出相应的源码。

1. 基本定义

// 邻接矩阵
typedef struct _graph
{
char vexs[MAX];       // 顶点集合
int vexnum;           // 顶点数
int edgnum;           // 边数
int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;

// 边的结构体
typedef struct _EdgeData
{
char start; // 边的起点
char end;   // 边的终点
int weight; // 边的权重
}EData;

Graph是邻接矩阵对应的结构体。

vexs用于保存顶点，vexnum是顶点数，edgnum是边数；matrix则是用于保存矩阵信息的二维数组。例如，matrix[i][j]=1，则表示”顶点i(即vexs[i])”和”顶点j(即vexs[j])”是邻接点；matrix[i][j]=0，则表示它们不是邻接点。

EData是邻接矩阵边对应的结构体。

转自 http://www.cnblogs.com/skywang12345/

2. 克鲁斯卡尔算法

模板1

/*
* 克鲁斯卡尔（Kruskal)最小生成树
*/
void kruskal(Graph G)
{
int i,m,n,p1,p2;
int length;
int index = 0;          // rets数组的索引
int vends[MAX]={0};     // 用于保存"已有最小生成树"中每个顶点在该最小树中的终点。
EData rets[MAX];        // 结果数组，保存kruskal最小生成树的边
EData *edges;           // 图对应的所有边

// 获取"图中所有的边"
edges = get_edges(G);
// 将边按照"权"的大小进行排序(从小到大)
sorted_edges(edges, G.edgnum);

for (i=0; i<G.edgnum; i++)
{
p1 = get_position(G, edges[i].start);   // 获取第i条边的"起点"的序号
p2 = get_position(G, edges[i].end);     // 获取第i条边的"终点"的序号

m = get_end(vends, p1);                 // 获取p1在"已有的最小生成树"中的终点
n = get_end(vends, p2);                 // 获取p2在"已有的最小生成树"中的终点
// 如果m!=n，意味着"边i"与"已经添加到最小生成树中的顶点"没有形成环路
if (m != n)
{
vends[m] = n;                       // 设置m在"已有的最小生成树"中的终点为n
rets[index++] = edges[i];           // 保存结果
}
}
free(edges);

// 统计并打印"kruskal最小生成树"的信息
length = 0;
for (i = 0; i < index; i++)
length += rets[i].weight;
printf("Kruskal=%d: ", length);
for (i = 0; i < index; i++)
printf("(%c,%c) ", rets[i].start, rets[i].end);
printf("\n");
}

模板2

#include<stdio.h>
#include<string.h>
#define inf 0x3f3f3f3f
int map[110][110],dis[110],visit[110];
/*
关于三个数组：map数组存的为点边的信息，比如map[1][2]=3，表示1号点和2号点的距离为3
dis数组存的为起始点与每个点的最短距离，比如dis[3]=5，表示起始点与3号点最短距离为5
visit数组存的为0或者1，1表示已经走过这个点。
*/
int n,m;
int dijstra()
{
int i,j,pos=1,min,sum=0;
memset(visit,0,sizeof(visit));//初始化为.，表示开始都没走过
for(i=1; i<=n; ++i)
{
dis[i]=map[1][i];
}
visit[1]=1;
dis[1]=0;
for(i=1; i<n; i++)
{
min=inf;
for(j=1; j<=n; ++j)
{
if(visit[j]==0&&min>dis[j])
{
min=dis[j];
pos=j;
}
}
visit[pos]=1;//表示这个点已经走过
for(j=1; j<=n; ++j)
{
if(visit[j]==0&&dis[j]>dis[pos]+map[pos][j])//更新dis的值
dis[j]=dis[pos]+map[pos][j];
}
}
return dis
;
}
int main()
{
int i,j;
while(~scanf("%d%d",&n,&m),n||m)//n表示n个点，m表示m条边
{
for(i=1; i<=n; ++i)
{
for(j=1; j<=n; ++j)
{
map[i][j]=inf;//开始时将每条边赋为最大值
}
}
int a,b,c;
for(i=1; i<=m; ++i)
{
scanf("%d%d%d",&a,&b,&c);
if(c<map[a][b])//防止有重边
map[a][b]=map[b][a]=c;
}
int count=dijstra();
printf("%d\n",count);
}
return 0;
}