GraphicsLab Project之Normal Mapping
2017-03-07 21:42
225 查看
作者:i_dovelemon
日期:2017-03-07
来源:CSDN
主题:Normal Map, Normal Mapping, Tangent Space

如果我们要以三角形建模的方式来对这种细节进行建模的话,一方面很复杂,另一方面如此细小的几何体渲染出来的效果应该也很杂乱。所以,图形学家便想出了通过一个二维数组来编码保存一个几何体表面细节的方案,以此来模拟具有丰富表面的物体。最初的时候,是通过一张高度图来保存一个物体表面高低不平的高低信息,然后以此信息作为渲染的依据,从而渲染出表面的微小细节。此种技术被称为Bump Mapping,后来衍生出更多的算法来模拟表面细节,并且将这些模拟表面细节的技术都统称为Bump
Mapping。我们今天要讨论的主题Normal Mapping就是Bump Mapping的一种。
更多关于Bump Mapping的信息,可以查看wiki上关于它的描述。
大体的思路就是上面描述的那样,从中可以看出一个很明显的要点,那就法线贴图是什么?
所以,我们将法线的XYZ值进行编码,以便于存放在对应纹素的RGB中。虽然纹理的格式有很多,但是我们一般都选择使用R8B8G8的格式,也就是说我们需要将[-1,1]的范围映射到[0,255]的范围里面来。这个映射可以通过简单的线性变换得来,即对于法线的每一个分量进行(N + 1) * 128这样的计算,那么结果自然就在[0,255]之间。同样的,当我们在GPU中访问该纹理的时候,也可以通过逆向的运算来得到实际的法线分量值,即:(T - 0.5) * 2.(注:shader中访问纹理的结果在[0,1]的范围里面)。
相对于一个表面来说,一个指向它正半空间的法线才是有效的法线(回忆一下光照方程就知道这点),所以法线值的Z分量总是为正值,所以法线贴图总体呈现蓝色(B分量总是大于128),如下图所示:

所以后面又有人提议将法线保存在模型空间中,由于模型空间是相对于模型本身定义的,不管在世界坐标系统中处于什么位置,朝向,法线都能够继续使用,只不过需要进行一些坐标变换的处理而已。这种方法比较实用,能够很大限度的使用法线贴图,但是同样的它也有缺点。即使是在模型空间中,我们也往往会对模型进行变形操作,比如动画系统,而一旦在模型空间中进行了变形,那法线贴图也将不再有效。所以将法线贴图定义在模型空间对于那些不会变形的物体能够很好的重复使用。在GLB中,目前还没有任何的动画系统,所以仅仅定义在模型空间中已经能够满足我们的需求,不过,GLB的目的是为了学习,既然知道有这个缺点,那么我们就得知道如何去解决它。最终发现可以将法线定义在切空间中(Tangent
Space)中。
既然我们知道了在切空间中保存法线是最好的选择,那么怎么定义这个切空间了?我们知道,要定义一个空间是需要一个参考系的,在知道参考系的情况下,明确切空间的XYZ轴在参考系坐标系统下的表示,就能够精确的定义这个切空间。对于切空间来说,最方便的选择就是选择模型空间做为参考系,也就是说,对于一个三角形来说,使用保存切空间的XYZ轴在模型空间中的表示,就能够定义这个三角形的切空间了。
首先要明确,三角形表面上定义的切空间有无数个,那么我们选取哪一个作为我们的切空间了?这个选择自然是要方便我们进行某种计算,那么将切空间的XY轴定义为与三角形纹理坐标系统的UV坐标轴对齐,Z轴为三角形表面的法线,这样的切空间就能够非常方便我们进行计算。对于切空间的XYZ轴,他们分别有专门的名字:Tangent, Binormal(BiTangent)和Normal,以下将使用T,B,N来表示,切空间的图形化表示如下图:
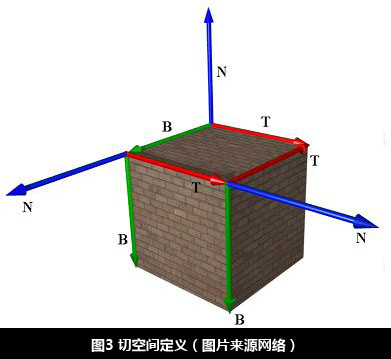
那么,我们怎么知道顶点的Tangent和Binormal属性了?
对于任意一个三角形,我们知道它的三个顶点的位置P0,P1,P2和对应的纹理坐标T0,T1,T2,那么就有如下的关系:
(1) P_E0 = P1 - P0
(2) P_E1 = P2 - P0
(3) T_E0 = T1 - T0
(4) T_E1 = T2 - T0
(5) P_E0 = T_E0.u * T + T_E0.v * B
(6) P_E1 = T_E1.u * T + T_E1.v * B
据此,我们就能够解出T和B向量出来。

我们知道,球面上法线的计算是通过共享的多个三角形面法线的平均值来进行计算的。这种计算方式是为了模拟平滑的参数曲面而提出,是一种近似的解决方案,在绝大多数时候都能够给我们带来很好的视觉效果。而由于实际在构建这个球体的时候,是使用离散的三角形来实现的,所以我们仅仅根据三角形求出来的TB向量,将丢失了平滑曲面的效果。既然球体中顶点的法线能够带来曲面的效果,那么我们可以将上面公式计算出来的T和B,和顶点的法线做一下正交化操作,这样就能够保证我们在球体上进行法线映射的时候,不会破坏平滑曲面的效果。
正交化的操作可以通过施密特正交化(Gram-Schmidt orthogonalization)来实现,计算方法如下:
T' = T - N * dot(N, T)
B' = B - N * dot(N, B)
很简单是不是?
在Vertex Shader中,我们将顶点属性的T,B,N都转化到世界空间中去,如下所示:
在Fragment Shader中,我们知道从纹理中获取法线,然后根据T,B,N构建转化矩阵,将法线转化到世界坐标即可,如下所示:
当一切准备就绪之后就可以来试验看看最终的效果如何:

[2] http://www.terathon.com/code/tangent.html ,
http://blog.csdn.net/fanbird2008/article/details/12401835 About Tangent Space
[3] http://www.tairan.com/archives/5976/ OpenGL3.0教程 第十三课: 法线贴图
日期:2017-03-07
来源:CSDN
主题:Normal Map, Normal Mapping, Tangent Space
引言
GraphicsLab(GLB)代码库之前只支持Diffuse贴图和Alpha贴图,想要做出更加精细的效果,需要增加对其他类型贴图的支持,所以最近将Normal贴图也整合到GLB中去。通过使用Normal贴图,在结合Normal Mapping的技术,我们就能够渲染带有更多微小细节的物体。凹凸映射(Bump Mapping)
自然界中存在很多具有丰富细节的表面,如石板面和墙壁:
如果我们要以三角形建模的方式来对这种细节进行建模的话,一方面很复杂,另一方面如此细小的几何体渲染出来的效果应该也很杂乱。所以,图形学家便想出了通过一个二维数组来编码保存一个几何体表面细节的方案,以此来模拟具有丰富表面的物体。最初的时候,是通过一张高度图来保存一个物体表面高低不平的高低信息,然后以此信息作为渲染的依据,从而渲染出表面的微小细节。此种技术被称为Bump Mapping,后来衍生出更多的算法来模拟表面细节,并且将这些模拟表面细节的技术都统称为Bump
Mapping。我们今天要讨论的主题Normal Mapping就是Bump Mapping的一种。
更多关于Bump Mapping的信息,可以查看wiki上关于它的描述。
法线映射(Normal Mapping)
Normal Mapping是Bump Mapping的一种。这种技术将一个粗糙表面上各个微小的细节编码成法线,保存在一张法线贴图上,然后在进行光照计算的时候,不使用从顶点属性插值过来的法线,而是从这张法线贴图上获取对应位置的法线进行光照计算。大体的思路就是上面描述的那样,从中可以看出一个很明显的要点,那就法线贴图是什么?
法线贴图(Normal Map)
我们知道,一个归一化的法线,它的XYZ坐标分量都在[-1,1]这个范围里面。而在渲染中创建查找表的方式,都是将我们所需要的信息放在一张纹理上,毕竟GPU能够很方便的访问纹理贴图。所以,我们将法线的XYZ值进行编码,以便于存放在对应纹素的RGB中。虽然纹理的格式有很多,但是我们一般都选择使用R8B8G8的格式,也就是说我们需要将[-1,1]的范围映射到[0,255]的范围里面来。这个映射可以通过简单的线性变换得来,即对于法线的每一个分量进行(N + 1) * 128这样的计算,那么结果自然就在[0,255]之间。同样的,当我们在GPU中访问该纹理的时候,也可以通过逆向的运算来得到实际的法线分量值,即:(T - 0.5) * 2.(注:shader中访问纹理的结果在[0,1]的范围里面)。
相对于一个表面来说,一个指向它正半空间的法线才是有效的法线(回忆一下光照方程就知道这点),所以法线值的Z分量总是为正值,所以法线贴图总体呈现蓝色(B分量总是大于128),如下图所示:

法线定义的空间
最初贴图中保存的法线,它的坐标定义是在世界空间中,这种做法对于那些静态的物体能够很有效的工作,但是对于那些动态的物体,一旦朝向发生了改变,那么这张法线贴图就没有办法再次使用了。所以后面又有人提议将法线保存在模型空间中,由于模型空间是相对于模型本身定义的,不管在世界坐标系统中处于什么位置,朝向,法线都能够继续使用,只不过需要进行一些坐标变换的处理而已。这种方法比较实用,能够很大限度的使用法线贴图,但是同样的它也有缺点。即使是在模型空间中,我们也往往会对模型进行变形操作,比如动画系统,而一旦在模型空间中进行了变形,那法线贴图也将不再有效。所以将法线贴图定义在模型空间对于那些不会变形的物体能够很好的重复使用。在GLB中,目前还没有任何的动画系统,所以仅仅定义在模型空间中已经能够满足我们的需求,不过,GLB的目的是为了学习,既然知道有这个缺点,那么我们就得知道如何去解决它。最终发现可以将法线定义在切空间中(Tangent
Space)中。
切空间(Tangent Space)
切空间描述
所谓的切空间,大家可以理解为是一个定义与三角形表面之上的一个空间。不管一个物体怎么变形,只要它还要进行光栅化操作,那么它必然是有一群三角形构成的,而三角形在变形过程中不可能发生弯曲,所以相对于这个三角形表面空间所定义的法线,在什么情况下都能够使用。既然我们知道了在切空间中保存法线是最好的选择,那么怎么定义这个切空间了?我们知道,要定义一个空间是需要一个参考系的,在知道参考系的情况下,明确切空间的XYZ轴在参考系坐标系统下的表示,就能够精确的定义这个切空间。对于切空间来说,最方便的选择就是选择模型空间做为参考系,也就是说,对于一个三角形来说,使用保存切空间的XYZ轴在模型空间中的表示,就能够定义这个三角形的切空间了。
首先要明确,三角形表面上定义的切空间有无数个,那么我们选取哪一个作为我们的切空间了?这个选择自然是要方便我们进行某种计算,那么将切空间的XY轴定义为与三角形纹理坐标系统的UV坐标轴对齐,Z轴为三角形表面的法线,这样的切空间就能够非常方便我们进行计算。对于切空间的XYZ轴,他们分别有专门的名字:Tangent, Binormal(BiTangent)和Normal,以下将使用T,B,N来表示,切空间的图形化表示如下图:

切空间定义
我们在上面已经知道了切空间的基本情况,那么我们如何使用精确的描述这个空间了。对于渲染来说,我们需要在顶点属性中额外的添加用于保存该顶点切空间信息的相关属性,我这里为了方便,添加了Tangent和Binormal属性,分别对应T,B坐标轴,有了这两个属性,我们通过Cross Product就能够计算出Normal轴。那么,我们怎么知道顶点的Tangent和Binormal属性了?
对于任意一个三角形,我们知道它的三个顶点的位置P0,P1,P2和对应的纹理坐标T0,T1,T2,那么就有如下的关系:
(1) P_E0 = P1 - P0
(2) P_E1 = P2 - P0
(3) T_E0 = T1 - T0
(4) T_E1 = T2 - T0
(5) P_E0 = T_E0.u * T + T_E0.v * B
(6) P_E1 = T_E1.u * T + T_E1.v * B
据此,我们就能够解出T和B向量出来。
切空间平滑
如果你仅仅依据上面的公式遍历每一个三角形,然后计算每一个三角形顶点的切空间向量T,B,这样的结果只有在当三角形顶点的法线与三角形面法线一致的时候才能够很好的作用(比如立方体)。但是对于那些具有共有顶点,导致顶点的法线是通过共有三角形面的平均值来定义的物体(比如球),使用上面公式计算出来的T,B进行Normal Mapping的时候,就会出现如下的情况:
我们知道,球面上法线的计算是通过共享的多个三角形面法线的平均值来进行计算的。这种计算方式是为了模拟平滑的参数曲面而提出,是一种近似的解决方案,在绝大多数时候都能够给我们带来很好的视觉效果。而由于实际在构建这个球体的时候,是使用离散的三角形来实现的,所以我们仅仅根据三角形求出来的TB向量,将丢失了平滑曲面的效果。既然球体中顶点的法线能够带来曲面的效果,那么我们可以将上面公式计算出来的T和B,和顶点的法线做一下正交化操作,这样就能够保证我们在球体上进行法线映射的时候,不会破坏平滑曲面的效果。
正交化的操作可以通过施密特正交化(Gram-Schmidt orthogonalization)来实现,计算方法如下:
T' = T - N * dot(N, T)
B' = B - N * dot(N, B)
很简单是不是?
Tangent,Binormal计算方法
前面的理论知识已经足够,现在来看看实际的代码吧。下面的代码取之GLB项目中的工具软件glb_tbn_gen,这个工具用来为.obj文件生成对应的tangent space坐标:bool glb_calc_tangent_binormal_coordinates(int32_t face_num, float* vertex_buf, float* texcoord_buf, float* normal_buf, std::vector<TangentSpace> &tangents) {
bool result = true;
if (vertex_buf == NULL || texcoord_buf == NULL) {
result = false;
return result;
}
glb::Vector v0, v1, v2, t0, t1, t2, n0, n1, n2;
for (int32_t i = 0; i < face_num; i++) {
v0.x = vertex_buf[i * 3 * 3 + 0 * 3 + 0];
v0.y = vertex_buf[i * 3 * 3 + 0 * 3 + 1];
v0.z = vertex_buf[i * 3 * 3 + 0 * 3 + 2];
v1.x = vertex_buf[i * 3 * 3 + 1 * 3 + 0];
v1.y = vertex_buf[i * 3 * 3 + 1 * 3 + 1];
v1.z = vertex_buf[i * 3 * 3 + 1 * 3 + 2];
v2.x = vertex_buf[i * 3 * 3 + 2 * 3 + 0];
v2.y = vertex_buf[i * 3 * 3 + 2 * 3 + 1];
v2.z = vertex_buf[i * 3 * 3 + 2 * 3 + 2];
t0.x = texcoord_buf[i * 3 * 2 + 0 * 2 + 0];
t0.y = texcoord_buf[i * 3 * 2 + 0 * 2 + 1];
t1.x = texcoord_buf[i * 3 * 2 + 1 * 2 + 0];
t1.y = texcoord_buf[i * 3 * 2 + 1 * 2 + 1];
t2.x = texcoord_buf[i * 3 * 2 + 2 * 2 + 0];
t2.y = texcoord_buf[i * 3 * 2 + 2 * 2 + 1];
n0.x = normal_buf[i * 3 * 3 + 0 * 3 + 0];
n0.y = normal_buf[i * 3 * 3 + 0 * 3 + 1];
n0.z = normal_buf[i * 3 * 3 + 0 * 3 + 2];
n1.x = normal_buf[i * 3 * 3 + 1 * 3 + 0];
n1.y = normal_buf[i * 3 * 3 + 1 * 3 + 1];
n1.z = normal_buf[i * 3 * 3 + 1 * 3 + 2];
n2.x = normal_buf[i * 3 * 3 + 2 * 3 + 0];
n2.y = normal_buf[i * 3 * 3 + 2 * 3 + 1];
n2.z = normal_buf[i * 3 * 3 + 2 * 3 + 2];
TangentSpace space;
glb_calc_tangent_binormal(v0, v1, v2, t0, t1, t2, n0, n1, n2, space);
tangents.push_back(space);
}
return result;
}
void glb_calc_tangent_binormal(glb::Vector v0, glb::Vector v1, glb::Vector v2
, glb::Vector t0, glb::Vector t1, glb::Vector t2
, glb::Vector n0, glb::Vector n1, glb::Vector n2
, TangentSpace& space) {
glb::Vector vedge0 = v1 - v0;
glb::Vector vedge1 = v2 - v0;
glb::Vector tedge0 = t1 - t0;
glb::Vector tedge1 = t2 - t0;
float temp = 1.0f / (tedge0.x * tedge1.y - tedge0.y * tedge1.x);
glb::Vector tangent = (vedge0 * tedge1.y - vedge1 * tedge0.y) * temp;
glb::Vector binormal = (vedge1 * tedge0.x - vedge0 * tedge1.x) * temp;
tangent.Normalize();
binormal.Normalize();
// Gram-Schmidt orthogonalize
space.tangent[0] = tangent - n0 * glb::Dot(n0, tangent);
space.binormal[0] = binormal - n0 * glb::Dot(n0, binormal);
space.tangent[1] = tangent - n1 * glb::Dot(n1, tangent);
space.binormal[1] = binormal - n1 * glb::Dot(n1, binormal);
space.tangent[2] = tangent - n2 * glb::Dot(n2, tangent);
space.binormal[2] = binormal - n2 * glb::Dot(n2, binormal);
}法线映射Shader
对于法线映射来说,主要的操作都是计算顶点属性的切空间坐标。当这个准备好了之后,我们就可以进行光照计算。计算的方式有很多,可以将光照向量,观察向量都转化到顶点的切空间来进行计算,也可以反向的将切空间中的法线转化到世界坐标系中来进行,在GLB库中选取的是后面一种做法。在Vertex Shader中,我们将顶点属性的T,B,N都转化到世界空间中去,如下所示:
uber.vs
#ifdef GLB_TANGENT_IN_VERTEX #ifdef GLB_BINORMAL_IN_VERTEX vs_NT = cross(glb_Tangent, glb_Binormal); vs_NT = (glb_Trans_Inv_WorldM * vec4(vs_NT, 0.0)).xyz; #endif #endif #ifdef GLB_TANGENT_IN_VERTEX vs_Tangent = (glb_Trans_Inv_WorldM * vec4(glb_Tangent, 0.0)).xyz; #endif #ifdef GLB_BINORMAL_IN_VERTEX vs_Binormal = (glb_Trans_Inv_WorldM * vec4(glb_Binormal, 0.0)).xyz; #endif
在Fragment Shader中,我们知道从纹理中获取法线,然后根据T,B,N构建转化矩阵,将法线转化到世界坐标即可,如下所示:
uber.ps
#ifdef GLB_ENABLE_NORMAL_MAPPING vec3 normal = texture2D(glb_NormalTex, vs_TexCoord).xyz; normal -= vec3(0.5, 0.5, 0.5); normal *= 2.0; mat3 tbn = mat3(vs_Tangent, vs_Binormal, vs_NT); normal = tbn * normal; normalize(normal); #endif
当一切准备就绪之后就可以来试验看看最终的效果如何:

总结
法线贴图的使用能够有效的为表面增添细节,能够是图像的质量更加的好。当然,法线贴图的功能不仅仅与此,为了更好的表现表面的凹凸感,后面还会讲述其他的技术来提升效果。参考文献
[1] https://en.wikipedia.org/wiki/Bump_mapping About Bump Mapping[2] http://www.terathon.com/code/tangent.html ,
http://blog.csdn.net/fanbird2008/article/details/12401835 About Tangent Space
[3] http://www.tairan.com/archives/5976/ OpenGL3.0教程 第十三课: 法线贴图
相关文章推荐
- GraphicsLab Project之辉光(Glare,Glow)效果
- GraphicsLab Project之Screen Space Ambient Occlusion(SSAO)
- GraphicsLab Project之HDR渲染
- GraphicsLab Project之Parallel Split Shadow Map(PSSM)
- CSIT-540 Spring 2007 - Project 4 - Benchmarking Graphics Hardware
- The requested resource (/lab-management/Project_Audit.Action) is not available.
- Computer Graphics Project2——画线及画圆
- Linux Lab and project latest
- Computer Graphics Project3(OpenGL实现机器人走动及层级结构)
- Project 2003 Service Pack 1
- python-loggingserver - A Python logging server based on Twisted - Google Project Hosting
- Face Judge Project
- Java compiler level does not match the version of the installed Java project facet.(转)
- Invalid project description.
- [导入]Why does my Windows Form project not use visual styles in XP even when I call Application.EnableVisualStyles?
- MyEclipse web project 重命名问题?(如何彻底修改工程名)
- myeclipse 2013 pro创建web Project时,没有web.xml文件
- Android Studio 去掉Instant Run, rebuild project,运行apk报内存溢出
- Project facet Cloud Foundry Standalone Application version 1.0 is not supported.
- CCIE(ROUTING AND SWITCHING) Lab 实验考试内容介绍
