bzoj 1013: [JSOI2008]球形空间产生器sphere（高斯消元）

1013: [JSOI2008]球形空间产生器sphere

Time Limit: 1 Sec Memory Limit: 162 MB

Submit: 4005 Solved: 2113

[Submit][Status][Discuss]

Description

　　有一个球形空间产生器能够在n维空间中产生一个坚硬的球体。现在，你被困在了这个n维球体中，你只知道球

面上n+1个点的坐标，你需要以最快的速度确定这个n维球体的球心坐标，以便于摧毁这个球形空间产生器。

Input

　　第一行是一个整数n(1<=N=10)。接下来的n+1行，每行有n个实数，表示球面上一点的n维坐标。每一个实数精确到小数点

后6位，且其绝对值都不超过20000。

Output

　　有且只有一行，依次给出球心的n维坐标（n个实数），两个实数之间用一个空格隔开。每个实数精确到小数点

后3位。数据保证有解。你的答案必须和标准输出一模一样才能够得分。

Sample Input

2

0.0 0.0

-1.0 1.0

1.0 0.0

Sample Output

0.500 1.500

HINT

　　提示：给出两个定义：1、 球心：到球面上任意一点距离都相等的点。2、 距离：设两个n为空间上的点A, B

的坐标为(a1, a2, …, an), (b1, b2, …, bn)，则AB的距离定义为：dist = sqrt( (a1-b1)^2 + (a2-b2)^2 +

… + (an-bn)^2 )

Source

题解：高斯消元。

先说一下思路：不再一条直线上的3个点可以确定一个唯一的圆（二维）

以此类推，如果是n 维的话，不在同一条直线上的n+1个点可以确定一个n维的球。

根据dist = sqrt( (a1-b1)^2 + (a2-b2)^2 + …
+ (an-bn)^2 ),我们就得到了n+1个方程。

以三维球为例，设球心坐标为（x,y,z),半径为r

方程组为 (x1-x)^2+(y1-y)^2+(z1-z)^2=r^2

(x2-x)^2+(y2-y)^2+(z2-z)^2=r^2

(x3-x)^2+(y3-y)^2+(z3-z)^2=r^2

(x4-x)^2+(y4-y)^2+(z4-z)^2=r^2

很明显这个方程是无法高斯消元的，因为存在二次项，所以我们需要把式子变形一下

以第一个方程作为一个标准 ，把第一个方程拆开

x1^2+x^2+y1^2+y^2+z1^2+z^2=2x1x+2y1y+2z1z

在把剩下的三个方程拆成这种形式，然后用每个方程与第一个方程左右分别做差就可以把所以未知量的二次项全部消去，得到 x2^2-x1^2+y2^2-y1^2+z2^2-z1^1(这些都是已知量，是个常数)=2(x2-x1)x+2(y2-y1)y+2(z2-z1)z

最终就可以得到N个线性方程，就可以用高斯消元求解。

高斯消元

高斯消元法是求解线性方阵组的一种算法，它也可用来求矩阵的秩（A=(aij)m×n的不为零的子式的最大阶数称为矩阵A的秩，记作rA，或rankA。），以及求可逆方阵的逆矩阵。它通过逐步消除未知数来将原始线性系统转化为另一个更简单的等价的系统。它的实质是通过初等行变化（，将线性方程组的增广矩阵转化为行阶梯矩阵。总结起来，如下步骤所示

以下面方程组为例，它的执行步骤为





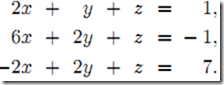
1）构造增广矩阵，即系数矩阵A增加上常数向量b（A|b）



2）通过以交换行、某行乘以非负常数和两行相加这三种初等变化将原系统转化为更简单的三角形式（triangular form）
注：这里的初等变化可以通过系数矩阵A乘上初等矩阵E来实现



3）从而得到简化的三角方阵组，注意它更容易解



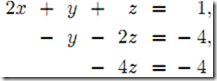
4）这时可以使用向后替换算法（Algorithm for Back Substitution）求解得
z=-4/-4=1, y=4-2z=4-2=2, x= (1-y-z)/2=(1-2-1)/2=-1

总结上面过程，高斯消元法其实就是下面非常简单的过程

原线性方程组 ——> 高斯消元法 ——> 下三角或上三角形式的线性方程组 ——> 前向替换算法求解（对于上三角形式，采用后向替换算法）

转换为行阶梯阵，判断解的情况。（这道题貌似不用）

① 无解

当方程中出现(0, 0, …, 0, a)的形式，且a != 0时，说明是无解的。

② 唯一解

条件是k = equ，即行阶梯阵形成了严格的上三角阵。利用回代逐一求出解集。

③ 无穷解。

条件是k < equ，即不能形成严格的上三角形，自由变元的个数即为equ – k，但有些题目要求判断哪些变元是不缺定的。

这里单独介绍下这种解法：

首先，自由变元有var - k个，即不确定的变元至少有var - k个。我们先把所有的变元视为不确定的。在每个方程中判断不确定变元的个数，如果大于1个，则该方程无法求解。如果只有1个变元，那么该变元即可求出，即为确定变元。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#define esp 1e-6
using namespace std;
int n;
double f[100],a[100][100];
bool gauss()
{
int now=1,to; double t;
for (int i=1;i<=n;i++)//枚举未知量
{
for (to=now;to<=n;to++)
if (fabs(a[to][i])>esp) break;//保证当前未知量的系数不为0
if (to>n) continue;
if (to!=now)
for (int j=1;j<=n+1;j++)
swap(a[to][j],a[now][j]);
t=a[now][i];
for (int j=1;j<=n+1;j++) a[now][j]/=t;
for (int j=1;j<=n;j++)//模拟手动消元的过程，消完之后应该每行至多只有一个未知量，a[i][n+1]就是这个未知量的答案
if (j!=now)
{
t=a[j][i];
for (int k=1;k<=n+1;k++)
a[j][k]-=t*a[now][k];
}
now++;
}
for (int i=now;i<=n;i++)
if (fabs(a[i][n+1])>esp) return 0;
return 1;
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++) scanf("%lf",&f[i]);
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
{
double t; scanf("%lf",&t);
a[i][j]=2*(t-f[j]);
a[i][n+1]+=t*t-f[j]*f[j];
}//预处理出初始矩阵
int k=gauss();
for (int i=1;i<=n-1;i++)
printf("%.3lf ",a[i][n+1]);
printf("%.3lf\n",a
[n+1]);
return 0;
}