您的位置：首页 > 其它

机器学习--EM算法求解高斯混合模型

2015-06-08 16:49 267 查看

本文转自：

http://blog.csdn.net/linkin1005/article/details/41212085

EM算法（Expection-Maximizationalgorithm，EM）是一种迭代算法，通过E步和M步两大迭代步骤，每次迭代都使极大似然函数增加。但是，由于初始值的不同，可能会使似然函数陷入局部最优。辜丽川老师和其夫人发表的论文：基于分裂EM算法的GMM参数估计（提取码：77c0）改进了这一缺陷。下面来谈谈EM算法以及其在求解高斯混合模型中的作用。

一、高斯混合模型（Gaussian MixtureModel， GMM）
之前写过高斯判别分析模型，利用参数估计的方法用于解决二分类问题。下面介绍GMM，它是对高斯判别模型的一个推广，也能借此引入EM算法。

假设样本集为
$\{x^{(1)},x^{(2)},...,x^{(m)}\}$
并且样本和标签满足联合分布
$p(x^{(i)},z^{(i)})=p(x^{(i)}|z^{(i)})p(z^{(i)})$

。这里：
$z^{(i)}$
服从多项式分布，即
$z^{(i)}\sim Multinomial(\phi)$
（
$\phi_{j}=p(z^{(i)}=j)$
，
$\phi_{j}\ge 0$

，
$\underset{j=1}{\overset{k}{\sum}}\phi_{j}=1$

），且
$z\in\{1,2,...,k\}$
；在
$z^{(i)}$
给定的情况下，
$x^{(i)}$
服从正态分布，即
$x^{(i)}|z^{(i)}=j\sim N(\mu_{j},\Sigma_{j})$
。这样的模型称为高斯混合模型。

该模型的似然函数为：

$\begin{aligned}l(\phi,\mu,\Sigma)&=\underset{i=1}{\overset{m}{\sum}}log\; p(x^{(i)};\phi,\mu,\Sigma)\\ &= \underset{i=1}{\overset{m}{\sum}}log \underset{z^{(i)}=1}{\overset{k}{\sum}}p(x^{(i)}|z^{(i)};\mu,\Sigma)p(z^{(i)};\phi) \end{aligned}$

如果直接令
$l(\phi,\mu,\Sigma)$
的各变量偏导为0，试图分别求出各参数，我们会发现根本无法求解。但如果变量
$z^{(i)}$
是已知的，求解便容易许多，上面的似然函数可以表示为：

$l(\phi,\mu,\Sigma)=\underset{i=1}{\overset{m}{\sum}}log\;p(x^{(i)}|z^{(i)};\mu,\Sigma)+log\;p(z^{(i)};\phi)$

利用偏导求解上述式，可分别得到参数
$\phi,\mu,\Sigma$
的值：

$\phi_{j}=\frac{1}{m}\underset{i=1}{\overset{m}{\sum}}\&hash;\{z^{(i)}=j\}$

$\mu_{j}=\frac{\underset{i=1}{\overset{m}{\sum}}\&hash;\{z^{(i)}=j\}x^{(i)}}{\underset{i=1}{\overset{m}{\sum}}\&hash;\{z^{(i)}=j\}}$

$\Sigma_{j}=\frac{\underset{i=1}{\overset{m}{\sum}}\&hash;\{z^{(i)}=j\}(x^{(i)}-\mu_{j})(x^{(i)}-\mu_{j})^T}{\underset{i=1}{\overset{m}{\sum}}\&hash;\{z^{(i)}=j\}}$

其中,#{ }为指示函数，表示满足括号内条件的数目。

那么，变量
$z^{(i)}$
无法通过观察直接得到，
$z^{(i)}$
就称为隐变量，就需要通过EM算法，求解GMM了。下面从Jensen不等式开始，介绍下EM算法：

二、 Jensen不等式（Jensen’s inequality）

引理：如果函数f的定义域为整个实数集，并且对于任意x或
$\overset{\rightarrow}{x}$
存在
$f''(x)\ge 0$
或函数的Hessian矩阵
$H\ge0$
，那么函数f称为凹函数。
$f''(x)> 0$
或函数的Hessian矩阵H>0，那么函数f为严格凹函数。
（存在
$f''(x)\le 0$
或函数的Hessian矩阵
$H\le0$
，那么函数f称为凸函数；如果
$f''(x)< 0$
或函数的Hessian矩阵
H<0，那么函数f为严格凸函数。）

定理：如果函数f是凹函数，X为随机变量，那么：

\ge&space;f(EX)]
$E[f(x)]\ge f(EX)$

不幸的是很多人都会讲Jensen不等式记混，我们可以通过图形的方式帮助记忆。下图中，横纵坐标轴分别为X和f(X)，f(x)为一个凹函数，a、b分别为变量X的定义域，E[X]为定义域X的期望。图中清楚的看到各个量的位置和他们间的大小关系。反之，如果函数f是凸函数，X为随机变量，那么：

\le&space;f(EX)]
$E[f(x)]\le f(EX)$

Jensen不等式等号成立的条件为：=X]
$E[X]=X$
，即X为一常数。

三、 EM算法

假设训练集
$\{x^{(1)},x^{(2)},...,x^{(m)}\}$
是由m个独立的样本构成。我们的目的是要对
$p(x,z)$
概率密度函数进行参数估计。它的似然函数为：

$\begin {aligned}l(\theta)&=\underset{i=1}{\overset{m}{\sum}}log\;p(x,\theta)\\ &=\underset{i=1}{\overset{m}{\sum}}log\underset{z}{\sum}p(x,z;\theta) \end{aligned}$

然而仅仅凭借似然函数，无法对参数进行求解。因为这里的随机变量
$z^{(i)}$
是未知的。

EM算法提供了一种巧妙的方式，可以通过逐步迭代逼近最大似然值。下面就来介绍下EM算法：

假设对于所有i，
$Q_{i}$
皆为随机变量
$z^{(i)}$
的分布函数。即：
$\sum_{Z}Q_{i}(z)=1,Q_{i}(z)\ge0$
。那么：

$\begin{aligned}l(\theta)&=\underset{i}{\sum}log \; p(x^{(i)};\theta)\\ &=\underset{i}{\sum}log\underset{z^{(i)}}{\sum}p(x^{(i)},z^{(i)};\theta)\quad\quad\quad\quad &(1)\\&=\underset{i}{\sum}log\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}&(2)\\ &\ge \underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}&(3) \end{aligned}$

其中第（2）步至第（3）步的推导就使用了Jensen不等式。其中：f(x)=log x，
$f''(x)=-\frac{1}{x^{2}}<0$
，因此为凸函数；
$\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$
表示随机变量为
$Q_{i}(z^{(i)})$
概率分布函数为
$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$
的期望。因此有：

)\ge&space;\underset{z^{(i)}\sim&space;Q_{i}}{E}[f(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})})]]
$f(\underset{z^{(i)}\sim Q_{i}}{E}[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}])\ge \underset{z^{(i)}\sim Q_{i}}{E}[f(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})})]$

这样，对于任意分布
$Q_{i}$
，（3）都给出了
$l(\theta)$
的一个下界。如果我们现在通过猜测初始化了一个
$\theta$
的值，我们希望得到在这个特定的
$\theta$
下，更紧密的下界，也就是使等号成立。根据Jensen不等式等号成立的条件，当
$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$
为一常数时，等号成立。即：

$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})} =c$

由上式可得
$p(x^{(i)},z^{(i)};\theta)=cQ_{i}(z^{(i)})$
，又
$\sum_{Z}Q_{i}(z)=1$
，因此
$p(x^{(i)},z^{(i)};\theta)=c$
。再由上式可得：

$\begin {aligned}Q_{i}(z^{(i)})&=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum_{z}{p(x^{(i)},z;\theta)}}\\&=\frac{p(x^{(i)},z^{(i)};\theta)}{{p(x^{(i)};\theta)}}\\&=p(z^{(i)}|x^{(i)};\theta) \end{aligned}$

上述等式最后一步使用了贝叶斯公示。

EM算法有两个步骤：

（1）通过设置初始化
$\theta$
值，求出使似然方程最大的
$Q_{i}$
值，此步骤称为E-步（E-step）

（2）利用求出的
$Q_{i}$
值，更新
$\theta$
。此步骤称为M-步（M-step）。过程如下：

repeat until convergence{

(E-step) for each i, set

$Q_{i}(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta)$

$Q_{i}(z^{(i)})=p(z^{(i)}|x^{(i)};\theta)$

(M-step) set

$\theta:=arg\,\underset{\theta}{max}\underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$

｝

那么，如何保证EM算法是收敛的呢？下面给予证明：

假设
$\theta^{(t)}$
和
$\theta^{(t+1)}$
是EM算法第t次和第t+1次迭代所得到的参数
$\theta$
的值，如果有
$l(\theta^{(t)})\le l(\theta^{(t+1)})$
，即每次迭代后似然方程的值都会增大，通过逐步迭代，最终达到最大值。以下是证明：

$\begin{aligned} l(\theta^{(t+1)}) &\ge \underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}^{(t)}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_{i}^{(t)}(z^{(i)})}\quad\quad&(4)\\ &\ge \underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}^{(t)}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_{i}^{(t)}(z^{(i)})}&(5)\\ &=l(\theta^{(t)})&(6) \end {aligned}$

不等式（4）是由不等式（3）得到，对于任意
$Q_{i}$
和
$\theta$
值都成立；得到不等式（5）是因为我们需要选择特定的
$\theta^{(t+1)}$
使得方程
$arg\,\underset{\theta}{max}\underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$
在
$\theta^{(t+1)}$
处的值大于在
$\theta^{(t)}$
处的值；等式（6）是找到特定的
$\theta^{(t)}$
的值，使得等号成立。

最后我们通过图形的方式再更加深入细致的理解EM算法的特点：

$J(Q,\theta)=\underset{i}{\sum}\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}$

由上文我们知道有这样的关系：
$l(\theta)\ge J(Q,\theta)$
，EM算法就是不断最大化这个下界，逐步得到似然函数的最大值。如下图所示：

首先，初始化
$\theta^{(0)}$
，调整
$Q(z)$
使得
$J(Q,\theta^{(0)})$
与
$l(\theta^{(0)})$
相等，然后求出
$J(Q,\theta^{(0)})$
使得到最大值的
$\theta^{(1)}$
；固定
$\theta^{(1)}$
，调整
$Q(z)$
，使得
$J(Q,\theta^{(1)})$
与
$l(\theta^{(1)})$
相等，然后求出使
$J(Q,\theta^{(1)})$
得到最大值的
$\theta^{(2)}$
；……；如此循环，使得
$l(\theta)$
的值不断上升，直到k次循环后，求出了
$l(\theta)$
的最大值
$l(\theta^{(k)})$
。

四、 EM算法应用于混合高斯模型（GMM）

再回到GMM：上文提到由于隐变量
$z^{(i)}$
的存在，无法直接求解参数，但可以通过EM算法进行求解：

E-Step:

$\omega_{j}^{(i)}=Q_{i}(z^{(i)}=j) =P(z^{(i)}=j|x^{(i)};\phi,\mu,\Sigma)$

M-Step:

$\begin{aligned} &\underset{i=1}{\overset{m}{\sum}}\underset{z^{(i)}}{\sum}Q_{i}(z^{(i)})log \frac{p(x^{(i)},z^{(i)};\phi,\mu,\Sigma)}{Q_{i}(z^{(i)})}\\ = &\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{k}{\sum}}Q_{i}(z^{(i)})log \frac{p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{Q_{i}(z^{(i)})}\\ = &\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{k}{\sum}}\omega_{j}^{(i)}log\frac{\frac{1}{(2\pi)^{\frac{n}{2}}\left|\Sigma_{j}\right|^\frac{1}{2}}exp(-\frac{1}{2}(x^{(i)}-\mu_{j})^{T}\Sigma_{j}^{-1}(x^{(i)}-\mu_{j}))\cdot\phi_{j}}{\omega_{j}^{(i)}} \end {aligned}$

（1）参数
$\mu$

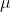
对期望
$\mu$
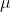
的每个分量
$\mu_{l}$
求偏导：

$\begin{aligned}&\triangledown_{\mu_{l}}\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{k}{\sum}}\omega_{j}^{(i)}log\frac{\frac{1}{(2\pi)^{\frac{n}{2}}\left|\Sigma_{j}\right|^\frac{1}{2}}exp(-\frac{1}{2}(x^{(i)}-\mu_{j})^{T}\Sigma_{j}^{-1}(x^{(i)}-\mu_{j}))\cdot\phi_{j}}{\omega_{j}^{(i)}}\\ =&-\triangledown_{\mu_{l}}\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{k}{\sum}}\omega_{j}^{(i)}\frac{1}{2}(x^{(i)}-\mu_{j})^{T}\Sigma_{j}^{-1}(x^{(i)}-\mu_{j})\\= &\frac{1}{2}\underset{i=1}{\overset{m}{\sum}}\omega_{l}^{(i)}\Delta_{\mu_{l}}(2\mu_{l}^{T}\Sigma_{l}^{-1}x^{(i)}-\mu_{l}^{T}\Sigma_{l}^{-1}\mu_{l})\\=&\underset{i=1}{\overset{m}{\sum}}\omega_{l}^{(i)}\Sigma_{l}^{-1}(x^{(i)}-\mu_{l}) \end{aligned}$

令上式为0，得：

$\mu_{l}:=\frac{\sum_{i=1}^{m}\omega_{l}^{(i)}x^{(i)}}{\sum_{i=1}^{m}{\omega_{l}^{(i)}}}$

（2）参数

观察M-Step，可以看到，跟
$\phi_{i}$
相关的变量仅仅有
$\omega_{j}^{(i)}$
。因此，我们仅仅需要最大化下面的目标函数：

$max\,\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{k}{\sum}}\omega_{j}^{(i)}log\phi_{j}$

又由于
$\sum_{j=1}^{k}\phi_{j}=1$
，为约束条件。因此，可以构造拉格朗日算子求目标函数：

$\mathcal L(\phi)=\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{k}{\sum}}\omega_{j}^{(i)}log\phi_{j}+\beta(\underset{j=1}{\overset{k}{\sum}}\phi_{j}-1)$

求偏导：

$\frac{\partial}{\partial \phi_{j}} \mathcal L(\phi)=\underset{i=1}{\overset{m}{\sum}}\frac{\omega_{j}{(i)}}{\phi_{j}}+1$

令
$\frac{\partial}{\partial \phi_{j}} \mathcal L(\phi)=0$
得：

$\phi_{j}:=\frac{\underset{i=1}{\overset{m}{\sum}}\omega_{j}^{(i)}}{-\beta}$

将
$\sum_{j=1}^{k}\phi_{j}=1$
带入上式得：

$\begin{aligned} -\beta=\sum_{i=1}^{m}\sum_{j=1}^{k}\omega_{j}^{(i)} &= \sum_{i=1}^{m}1 &=m\end{aligned}$

最后将
$\beta=-m$
带入得：

$\phi_{j}:=\frac{\underset{i=1}{\overset{m}{\sum}}\omega_{j}^{(i)}}{m}$

（3）参数
$\Sigma$

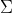
\\=&\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{m}{\sum}}\omega_{j}^{(i)}\frac{1}{2}\Sigma_{j}^{-T}+\frac{1}{2}(x^{(i)}-\mu_{j})^{T}\Sigma^{-2}(x^{(i)}-\mu_{j})&space;\end{aligned}]
$\begin{aligned}&\triangledown _{\Sigma_{j}} \underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{k}{\sum}}\omega_{j}^{(i)}log\frac{\frac{1}{(2\pi)^{\frac{n}{2}}\left|\Sigma_{j}\right|^\frac{1}{2}}exp(-\frac{1}{2}(x^{(i)}-\mu_{j})^{T}\Sigma_{j}^{-1}(x^{(i)}-\mu_{j}))\cdot\phi_{j}}{\omega_{j}^{(i)}}\\ =&\triangledown_{\Sigma_{j}}\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{k}{\sum}} \omega_{j}^{(i)}[-\frac{n}{2}log2\pi-\frac{1}{2}log\left|\Sigma_{j}\right|-\frac{1}{2}(x^{(i)}-\mu_{j})^{T}\Sigma_{j}^{-1}(x^{(i)}-\mu_{j})+log\phi_{j}-log\omega_{j}^{(i)}]\\=&\underset{i=1}{\overset{m}{\sum}}\underset{j=1}{\overset{m}{\sum}}\omega_{j}^{(i)}\frac{1}{2}\Sigma_{j}^{-T}+\frac{1}{2}(x^{(i)}-\mu_{j})^{T}\Sigma^{-2}(x^{(i)}-\mu_{j}) \end{aligned}$

令上式为零，解得：

$\Sigma_{j}:=\frac{\sum_{i=1}^{m}\omega_{j}^{(i)} (x^{(i)}-\mu_{j})(x^{(i)}-\mu_{j})^{T} }{ \sum_{i=1}^{m}\omega_{j}^{(i)} }$

五、总结

EM算法利用不完全的数据，进行极大似然估计。通过两步迭代，逐渐逼近最大似然值。而GMM可以利用EM算法进行参数估计。

最后提下辜老师论文的思路：EM模型容易收敛到局部最大值，并且严重依赖初试值。传统的方法即上文中使用的方法是每次迭代过程中，同时更新高斯分布中所有参数，而辜老师的方法是把K个高斯分布中的一个分量，利用奇异值分解的方法将其分裂为两个高斯分布，并保持其他分量不变的情况下，对共这K+1个高斯分布的权值进行更新，直到符合一定的收敛条件。这样一来，虽然算法复杂度没有降低，但每轮只需要更新两个参数，大大降低了每轮迭代的计算量。

内容来自用户分享和网络整理，不保证内容的准确性，如有侵权内容，可联系管理员处理

标签：

相关文章推荐

新的分享

章节导航