2014.5.1 训练日志(上午):动态规划(dp)
2014-05-01 13:40
204 查看
动态规划:
动态规划主要用于最优化(最大或最小)问题。目的是找出最优解值(可能有多个最优解)。它是一种思想,在程序设计中,已经抽象为一种程序设计技术,通常分为两个要素:最优子结构和重叠子问题。
最优子结构:
一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。我们通常可以将最优子结构归纳成递推关系式。
重叠子问题:
当我们用分治法将问题进行分解时,并不是所有的问题都是互相独立的,它们有重叠的部分,我们就将这些重叠的部分称作重叠子问题。如果这个时候运用递归将问题求解,势必要重复计算这些共享子问题。所以我们将这些子问题的结果保存起来,就避免了重复计算这些子问题,优化时间。
先看一题:
Longest Ordered Subsequence(最长上升子序列)
问题描述:
给出一个序列,求它最长的上升子序列.例如,序列{1,7,3,5,9,4,8},其中{1,7},{3,4,8},{1,3,5,8},都是它的上升子序列,而{1,3,5,8}是它的最长的上升子序列。
如果用DP应该怎样考虑?可以用以下的方式分步思考:
1、这个问题是否可以分解?
2、是否存在要重复做的问题?如果存在,是什么?
3、怎样做可以使每一个子问题都是最优的?【重要】
解题思路:
先设置f[i]表示当前位置时得到的最长公共子序列,a[i]记录位置,如下表:
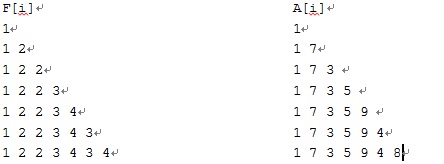
第一次循环时,A[i]检测相应的上升子序列。
第二次循环时,判断i=2时F[2]得到的最长序列。
第n 次循环时,判断i=n时F
得到的最长序列。
由此可得->
1、可以把问题分解成求到第i个(1<i<n)位置的最长升序子序列
2、于i的值位置的最大升序子序列,这是一个重复的问题。
3、dp[i]表示第i个位置的最优解,a[i]表示第i个位置的值。这样,可以得到一个递推式:dp[i]=max{dp[j]}+1(a[i]值大于a[j]&&j<i)
实现代码如下:(POJ 2533)
这是对于一维数组的DP,那么对于其他情况的DP,使用的是同样的思想,又应该怎样处理呢?
再看一题:
数塔
有形如下图所示的数塔,从顶部出发,在每一结点可以选择向左走或是向右走,一直走到底层,要求找出一条路径,使路径上的值最大。
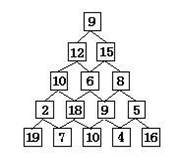
如果在向下走时,已经知道向哪边走最优,那么就不需要枚举多种情况了。也就是说:每一层的走向要取决于其下一层上的最大值。这样一层一层推下去,直到倒数第二层时就非常明了。例如,我们从最底层向上,将每次的最大值赋值给上一层,递推上去,直到第一层,如图:
第5层的1,2个数为19和7,那么第4层第一个数就应该是21,表示从第四层第一个数向下走时应该选择向左。 1)
第5层的2,3个数为7和10,那么第4层第二个数就应该是28,表示从第四层第二个数向下走时应该选择向右。 2)
所以第4层的1,2个数为21,28,那么第3层第一个数就应该是38,表示从第三层第一个数向下走时应该选择向右。
以此类推......
可以发现,在这里,我们将一个大问题不停地向下划分,分成了不同阶段的小问题;而每一阶段的问题的求解又依赖其划分的小问题的结果,我们将每个小问题的结果保存起来,需要用到时,就提取出来而不需要再一次求解
数塔中,每一层的最优解就是不同阶段的小问题,我们从后一层(最小的问题)开始解决,保存结果。而上一层要用到时,就将结果提供,而不需要再一次求解。而如果用枚举,则每个小问题都被重复的执行了多次。
eg.数塔问题中,重叠子问题就是对于每一层的下面层的最优解,我们用a[][]将其保存下来,从而节省了时间。
a[i][j]表示从第i层第j个结点开始求解时,其最大值;b[i][j]表示第i层的第j个结点的值,
其最优子结构为:ai][j]= max{a[i+1][j],a[i+1][j+1]}+b[i][j];
DP定义总结:
实际上,动态规划的实质就是通过保存计算过的状态,来避免递归的重叠子问题.解决冗余,是动态规划的根本目的.
动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种 状态,所以它的空间复杂度要大于其它的算法。
Dynamic programming is a story of past and future
The future is determined by the past
Each state is the summary of its past
动态规划主要用于最优化(最大或最小)问题。目的是找出最优解值(可能有多个最优解)。它是一种思想,在程序设计中,已经抽象为一种程序设计技术,通常分为两个要素:最优子结构和重叠子问题。
最优子结构:
一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。我们通常可以将最优子结构归纳成递推关系式。
重叠子问题:
当我们用分治法将问题进行分解时,并不是所有的问题都是互相独立的,它们有重叠的部分,我们就将这些重叠的部分称作重叠子问题。如果这个时候运用递归将问题求解,势必要重复计算这些共享子问题。所以我们将这些子问题的结果保存起来,就避免了重复计算这些子问题,优化时间。
先看一题:
Longest Ordered Subsequence(最长上升子序列)
问题描述:
给出一个序列,求它最长的上升子序列.例如,序列{1,7,3,5,9,4,8},其中{1,7},{3,4,8},{1,3,5,8},都是它的上升子序列,而{1,3,5,8}是它的最长的上升子序列。
如果用DP应该怎样考虑?可以用以下的方式分步思考:
1、这个问题是否可以分解?
2、是否存在要重复做的问题?如果存在,是什么?
3、怎样做可以使每一个子问题都是最优的?【重要】
解题思路:
先设置f[i]表示当前位置时得到的最长公共子序列,a[i]记录位置,如下表:

第一次循环时,A[i]检测相应的上升子序列。
第二次循环时,判断i=2时F[2]得到的最长序列。
第n 次循环时,判断i=n时F
得到的最长序列。
由此可得->
1、可以把问题分解成求到第i个(1<i<n)位置的最长升序子序列
2、于i的值位置的最大升序子序列,这是一个重复的问题。
3、dp[i]表示第i个位置的最优解,a[i]表示第i个位置的值。这样,可以得到一个递推式:dp[i]=max{dp[j]}+1(a[i]值大于a[j]&&j<i)
实现代码如下:(POJ 2533)
#include <iostream>
using namespace std;
int a[100],dp[100];
int main()
{
int n;
while(cin>>n)
{
for(int i=0;i<n;i++)
{
cin>>a[i];
dp[i]=1; //每个位置最长公共子序列为1
}
for(int i=0;i<n;i++)
{
int maxn=0;
for(int j=0;j<i;j++)
if( a[j] < a[i] && dp[j] > maxn ) maxn=dp[j];
dp[i]=maxn+1;
}
int res=0;
for(int k=0;k<n;k++)
if(res<dp[k]) res=dp[k]; //取出最长的上升子序列
cout<<res<<endl;
}
return 0;
}这是对于一维数组的DP,那么对于其他情况的DP,使用的是同样的思想,又应该怎样处理呢?
再看一题:
数塔
有形如下图所示的数塔,从顶部出发,在每一结点可以选择向左走或是向右走,一直走到底层,要求找出一条路径,使路径上的值最大。

如果在向下走时,已经知道向哪边走最优,那么就不需要枚举多种情况了。也就是说:每一层的走向要取决于其下一层上的最大值。这样一层一层推下去,直到倒数第二层时就非常明了。例如,我们从最底层向上,将每次的最大值赋值给上一层,递推上去,直到第一层,如图:
第5层的1,2个数为19和7,那么第4层第一个数就应该是21,表示从第四层第一个数向下走时应该选择向左。 1)
第5层的2,3个数为7和10,那么第4层第二个数就应该是28,表示从第四层第二个数向下走时应该选择向右。 2)
所以第4层的1,2个数为21,28,那么第3层第一个数就应该是38,表示从第三层第一个数向下走时应该选择向右。
以此类推......
可以发现,在这里,我们将一个大问题不停地向下划分,分成了不同阶段的小问题;而每一阶段的问题的求解又依赖其划分的小问题的结果,我们将每个小问题的结果保存起来,需要用到时,就提取出来而不需要再一次求解
数塔中,每一层的最优解就是不同阶段的小问题,我们从后一层(最小的问题)开始解决,保存结果。而上一层要用到时,就将结果提供,而不需要再一次求解。而如果用枚举,则每个小问题都被重复的执行了多次。
#include <iostream>
using namespace std;
int a[100][100],dp[100][100];
int main()
{
int n;
cin>>n;
for(int k=1;k<=n;k++)
for (int i=1;i<=k;i++)
cin>>a[k][i];
for(int k=1;k<=n;k++)
dp
[k]=a
[k];
for(int g=n-1;g>=1;g--)
{
for(int i=1;i<=g;i++)
{
if(dp[g+1][i]<dp[g+1][i+1]) dp[g][i]=a[g][i]+dp[g+1][i+1];
else dp[g][i]=a[g][i]+dp[g+1][i];
}
}
cout<<dp[1][1]<<endl;
return 0;
}eg.数塔问题中,重叠子问题就是对于每一层的下面层的最优解,我们用a[][]将其保存下来,从而节省了时间。
a[i][j]表示从第i层第j个结点开始求解时,其最大值;b[i][j]表示第i层的第j个结点的值,
其最优子结构为:ai][j]= max{a[i+1][j],a[i+1][j+1]}+b[i][j];
DP定义总结:
实际上,动态规划的实质就是通过保存计算过的状态,来避免递归的重叠子问题.解决冗余,是动态规划的根本目的.
动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种 状态,所以它的空间复杂度要大于其它的算法。
Dynamic programming is a story of past and future
The future is determined by the past
Each state is the summary of its past
相关文章推荐
- 2014.5.1 训练日志(下午):动态规划(DP)
- SDAU训练日志第14篇----------动态规划(10)(2018年2月11日)
- 蓝桥杯 ALGO-3 算法训练 K好数 (动态规划 DP)
- 蓝桥杯 K好数 算法训练 (动态规划DP)
- SDAU训练日志第八篇----------动态规划(4)(2018年2月5日)
- SDAU训练日志第十篇----------动态规划(6)(2018年2月7日)
- SDAU训练日志第12篇----------动态规划(8)(2018年2月9日)
- SDAU训练日志第七篇----------动态规划(3)(2018年2月4日)
- 寒假训练2018.2.3--2.5训练日志------dp学习
- SDAU训练日志第九篇----------动态规划(5)(2018年2月6日)
- 2018.1.19 训练日志--区间dp
- SDAU训练日志第15篇----------动态规划(11)(2018年2月12日)
- ACM暑假训练 3426: Hoof, Paper, Scissors (三维dp动态规划)
- 寒假训练2018.2.6训练日志------dp学习(一)
- SDAU训练日志第17篇----------动态规划(13)(2018年2月23日)
- SDAU训练日志第五篇----------动态规划(1)(2018年2月2日)
- SDAU训练日志第11篇----------动态规划(7)(2018年2月8日)
- 寒假训练2018.2.7训练日志------dp学习(二)尼克的任务
- [zz] POJ 动态规划DP题目列表
- 算法训练 K好数 [动态规划]
