关系数据理论必备知识点

前备知识

函数依赖

在属性集U上，X、Y都是U上的子属性集，如果可以根据属性集X中属性的值唯一确定属性集Y中属性的值，则称Y函数依赖于X，记做X→YX\to YX→Y.

比如说：

实例1：属性集

U={学号，姓名，年龄}

，

{学号}

和

{姓名}

都是属性集U上的子集，当给定一个学号的值时，可以唯一个姓名的值，这样就符合函数依赖的关系，我们说

{姓名}

函数依赖于

{学号}

，即学号姓名{学号}→{姓名}学号姓名\{学号\}\to \{姓名\}学号姓名{学号}→{姓名}。

实例2：还有一种情况，比如说

X={学号,姓名}

，

Y={姓名}

，当给定一个X的值时，也可以唯一确定Y的值，也有Y函数依赖于X，即学号姓名姓名{学号,姓名}→{姓名}学号姓名姓名\{学号,姓名\}\to\{姓名\}学号姓名姓名{学号,姓名}→{姓名}

可以发现实例2中Y是X的子集，即Y⊆XY \subseteq XY⊆X，这种情况我们称X→YX\to YX→Y是平凡的函数依赖，而对于实例1，Y⊆XY \subseteq XY⊆X不成立，这种情况下我们称X→YX\to YX→Y是非平凡的函数依赖。

完全函数依赖

在

R(U)

中，如果Y函数依赖于X但是Y不函数依赖于X的任何子集，则称Y完全函数依赖于X，记为X→FYX\stackrel{F} \to YX→FY,否则称Y部分依赖于X，记做X→PYX \stackrel{P} \to YX→PY。

比如属性集U中有3个属性：{a,b,c}\{a,b,c\}{a,b,c}，如果{a,b}→{c}\{a,b\}\to \{c\}{a,b}→{c}，且{a}→{c}\{a\} \to \{c\}{a}→{c}，就不能说c{c}c完全函数依赖于，{a，b}，\{a，b\}，{a，b}，反过来，如果 {a,b}→{c}\{a,b\} \to \{c \}{a,b}→{c} ，但 {a}↛{c}\{a\} \nrightarrow \{c\}{a}↛{c} 且{b}↛{c}\{b\} \nrightarrow \{c\}{b}↛{c}，则说明{c}完全函数依赖于{a,b}，即{a,b}→F{c}\{a,b\}\stackrel{F} \to \{c\}{a,b}→F{c}.

传递函数依赖

在R(U)中，如果X→Y,Y↛X,Y→ZX \to Y , Y \nrightarrow X,Y\to ZX→Y,Y↛X,Y→Z，则称Z传递函数依赖于X，记为传递X→传递Z传递X \stackrel{传递} \to Z传递X→传递Z.

注意这里一定要满足条件 Y↛XY \nrightarrow XY↛X，如果Y→XY\to XY→X，则有X↔YX \leftrightarrow YX↔Y ，这时就是X→ZX\to ZX→Z，而不是传递X→传递Z传递X \stackrel{传递} \to Z传递X→传递Z.

候选码

设K为R(U)中的属性或属性集合，若K→FUK\stackrel{F} \to UK→FU，则称K为R的候选码.

其实说白了，候选码就是最小的可以推出U中所有属性的集合，也就是说，如果确定了一组候选码的值，可以唯一确定一组U中所有属性的值，举个例子，

U={a,b,c,d}

，如果

{a,b}

的属性值确定后可以唯一确定

{c,d}

的值，即{a,b}→{c,d}\{a,b\}\to \{c,d\}{a,b}→{c,d}，则{a，b}就是一组候选码（因为{a,b}→{a,b}\{a,b\} \to \{a,b\}{a,b}→{a,b}一定是成立的，又有{a,b}→{c,d}\{a,b\}\to \{c,d\}{a,b}→{c,d}，所以{a,b}→{a,b,c,d}\{a,b\} \to \{a,b,c,d\}{a,b}→{a,b,c,d}即{a,b}→U\{a,b\} \to U{a,b}→U）。

主属性

我们说候选码是最小的可以推出U中所有属性的集合，而这个集合中的任意一个属性值，就称为主属性，而在集合U中但不在候选码集合中的属性称为非主属性。

多值依赖

多值依赖比较抽象，这里用一张图解释：

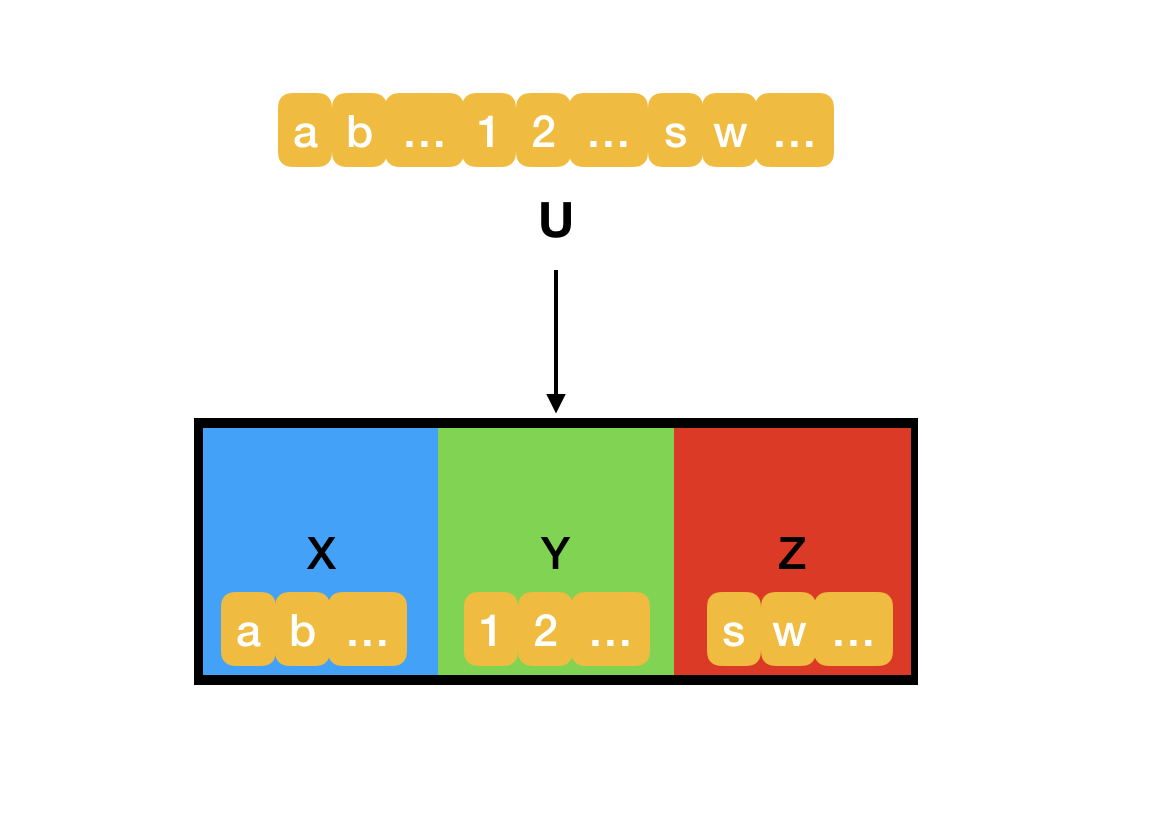
如上图所示，我们假设

R(U)

是属性集U上的一个关系模式，将U划分为3个子集X、Y、Z，注意这里的X、Y、Z是三个子集，每一个子集中都可能含有若干个属性，且X、Y、Z、U满足X∩Y=ϕ,X∩Z=ϕ,Y∩Z=ϕ,X∪Y∪Z=UX\cap Y =\phi ,X\cap Z=\phi ,Y \cap Z=\phi ,X\cup Y \cup Z=UX∩Y=ϕ,X∩Z=ϕ,Y∩Z=ϕ,X∪Y∪Z=U，即X、Y、Z两两不相交、X、Y、Z之并为U(图上画的很清楚了)。

如果X，Y，Z满足X可以决定Z的值且Y和Z没有任何关系（Y的值变化不会引起Z的值变化），则称Z多值依赖于X，记为X→→ZX \to \to ZX→→Z.

多值依赖有以下几个特性：

1. 对称性

   如上图所示，如果X→→ZX \to \to ZX→→Z，则必有X→→YX \to \to YX→→Y.

2. 传递性

   如果X→→{a},{a}→{a,b,c}X\to \to \{a\},\{a\} \to \{a,b,c\}X→→{a},{a}→{a,b,c}，则X→→{b,c}X \to \to \{b,c\}X→→{b,c}.

1NF

一阶范式(1NF)的定义：关系中每一个分量都不可再分，则这样的关系模式属于第一范式(1NF)，即**"键值"对中的"值“**应该为单个数值，而不是集合。

比如如下关系模式：

这样的关系模式就不属于第一范式，因为A1→b1,b2,b3A1\to{b1,b2,b3}A1→b1,b2,b3，b1,b2,b3还可再分，若想将其变为第一范式，则应该：

这时这个关系模式就属于第一范式。

2NF

**二阶范式(2NF)**的定义：在1NF的基础上，消除关系模式中非主属性对候选码的部分函数依赖后，称该关系模式为2NF。

考虑下表：

可以发现，我们通过学生编号就可以确定出来学生姓名、班级编号、学生院系，即：
{学生编号}→{学生姓名，班级编号，学生院系} \{学生编号\}\to \{学生姓名，班级编号，学生院系\} {学生编号}→{学生姓名，班级编号，学生院系}
我们发现除了这个函数依赖，还有课程编号、成绩这两个属性没有用到，也就是说我们可以得出:
{学生编号，课程编号，成绩}→{学生姓名，班级编号，学生院系} \{学生编号，课程编号，成绩\}\to \{学生姓名，班级编号，学生院系\} {学生编号，课程编号，成绩}→{学生姓名，班级编号，学生院系}

综合(1)式和(2)式，我们可以得出学生姓名，班级编号，学生院系{学生姓名，班级编号，学生院系}学生姓名，班级编号，学生院系\{学生姓名，班级编号，学生院系\}学生姓名，班级编号，学生院系{学生姓名，班级编号，学生院系}部分函数依赖于学生编号{学生编号}学生编号\{学生编号\}学生编号{学生编号}这个结论，则当前关系模式就不满足2NF的条件，即不属于2NF。

那么我们如何将上述关系模式转化为满足2NF要求的关系模式呢？自然是消除关系模式中非主属性对候选码的部分函数依赖，我们发现，上述关系模式不是2NF的原因在于学生姓名，班级编号，学生院系{学生姓名，班级编号，学生院系}学生姓名，班级编号，学生院系\{学生姓名，班级编号，学生院系\}学生姓名，班级编号，学生院系{学生姓名，班级编号，学生院系}部分函数依赖于学生编号{学生编号}学生编号\{学生编号\}学生编号{学生编号}，再进一步，是因为上述关系模式中出现了课程编号、成绩这两个属性，那么我们将这两个属性单独分离出来即可打破这种部分函数依赖，即将上面拆分为下面两个表格：

学生表：

学生-课程表：

这样就消除了关系模式中非主属性对候选码的部分函数依赖，该关系模式就属于2NF了。

3NF

定义：在1NF的基础上消除了非主属性对候选码的传递函数依赖后即满足3NF的要求。

以下表为例：

上表中主属性、候选码为学生编号，其他3个属性为非主属性，我们发现根据学生编号可以唯一确定院系，即院系函数依赖于学生编号，但是思考一下，我们是拿到学生编号后就能直接查出来所属院系吗？实际的流程应该是先根据学生编号确定班级编号，然后再根据班级编号确定院系，即从学生编号确定院系这个过程经历了班级编号这一中间属性，即院系是传递函数依赖于学生编号的，所以说，上表是不满足3NF的要求的。

要将一个关系模式转化为3NF，需要消除非主属性对候选码的传递函数依赖，对上表来说就是要消除院系对学生编号的传递函数依赖，那我们直接将院系和学生编号划分到两个表中就可以了，就像这样：

学生表：

班级-院系表：

这样该关系模式中就不存在非主属性对候选码的传递函数依赖了，就满足3NF的要求了。

BCNF

定义：在1NF的基础上，将主属性对候选码的部分函数依赖、传递函数依赖消除后，就满足了BCNF的要求，如果这么说不够明白，我们换种说法，如果每一个函数依赖的决定因素都包含候选码，则满足BCNF的要求，也就是说，对于关系模式中的任意一个函数依赖X→YX\to YX→Y，如果X中都含有候选码，则该关系模式属于BCNF。

在理解定义之前我们先明确主属性和候选码的区别，我们说，如果从一个属性集合X出发可以确定所有属性集U中属性的值，就称X为该关系模式的候选码，即候选码是一个集合，而候选码集合中的属性称为主属性。

我们以一个例子来说明BCNF：

关系模式R(U)，属性集U={a,b,c}，有如下依赖关系：
{a,b}→{c}{c}→{a} \{a,b\} \to \{c\}\\ \{c\} \to \{a\} {a,b}→{c}{c}→{a}
很明晰在这个关系模式中{a,b}为候选码，a，b为主属性，那么它是否符合BCNF范式的要求呢？我们再看一遍BCNF范式的要求：每一个函数依赖的决定因素都包含候选码

对于第一个函数依赖：{a,b}→{c}\{a,b\} \to \{c\}{a,b}→{c}，其决定因素{a,b}\{a,b\}{a,b}包含了候选码，没有问题；

对于第二个函数依赖：{c}→{a}\{c\} \to \{a\}{c}→{a}，其决定因素是{c}\{c\}{c}，可是这个决定因素没有包含候选码即{a,b}\{a,b\}{a,b}，所以这个函数依赖破坏了BCNF范式的要求。

那么我们如何将上述关系模式转化为满足BCNF范式要求的关系模式呢？方法和之前范式的规范化相同，很明显我们可以将(3)式转化为一张表：
{a,b}→{c} \{a,b\} \to \{c\} {a,b}→{c}

这个关系模式不满足BCNF范式要求的原因在于{c}→{a}\{c\} \to \{a\}{c}→{a}，那么我们可以将上表拆分为两个表，即：
{c}→{a} \{c\} \to \{a\} {c}→{a}

4NF

定义：在1NF的基础上消除了非平凡且非函数依赖的多值依赖后即满足4NF的要求，再进一步，对于关系模式中的每个非平凡多值依赖的决定因素都包含候选码，则满足4NF的要求，这一点和BCNF范式的要求类似，只是BCNF范式是相对于函数依赖所做的要求，这里是相对于多值依赖所做的要求。

比如现在有关系模式R(U)，U={课程，教师，参考书}，该关系模式的依赖关系可总结为：
{课程}→{参考书}{教师}→{教师} \{课程\} \to \{参考书\}\\ \{教师\} \to \{教师\}\\ {课程}→{参考书}{教师}→{教师}
即候选码为{课程}、{教师}。

另外注意，且满足{课程}、{教师}、{参考书}三个子集之交为空、之并为U，这样可以得到：
{课程}→FF{参考书} \{课程\} \stackrel{FF}\to \{参考书\} {课程}→FF{参考书}
{课程}中包含了候选码{课程}，所以有{参考书}多值依赖于{课程}，即课程参考书{课程}→→{参考书}课程参考书\{课程\} \to \to \{参考书\}课程参考书{课程}→→{参考书}.

而该关系模式中只有上述一个多值依赖，所以该关系模式属于4NF。

规范化总结

1. 注意各个范式之间的关系：

   

2. 将一个非xNF转化为xNF的方法是对原有的关系模式进行分解，比如将1个关系模式分解为n个

数据依赖的公理系统

对于一个关系模式R，其属性集为U、函数依赖集为F，如果对其中的任何一个关系r中的两个元组t，s，满足若t[X]=s[X]，则t[Y]=s[Y]，则称F逻辑蕴含X→YX \to YX→Y。

可能大家看这个概念比较抽象，我们先来明确两个概念 ：

关系： 实体与实体之间的联系，在数据表中就是列的组合，比如{学号，姓名，年级}这就是一组关系，描述的是学号、姓名、年级这三个实体之间的联系。

元组： 数据表中每一行就是一个元组，比如{161610000,张三，一年级}这就是上述关系的一个元组

明确了这两个概念之后我们以上述实例来理解一下什么是F逻辑蕴含X→YX \to YX→Y：对于一张表，有3列，分别为学号、姓名、年级，其函数依赖集为：
F={{学号}→{姓名}{学号}→{年级}} F=\{\\ \{学号\} \to \{姓名\}\\ \{学号\} \to \{年级\}\\ \} F={{学号}→{姓名}{学号}→{年级}}

对于其中的任意两行（记为第t行和第s行），如果第t行和第s行的学号值相同，就有第s行的姓名值和第s行的姓名值相同，则称F逻辑蕴含学号姓名{学号}→{姓名}学号姓名\{学号\} \to \{姓名\}学号姓名{学号}→{姓名}，即函数依赖集F中蕴含的函数依赖为学号姓名{学号}→{姓名}学号姓名\{学号\} \to \{姓名\}学号姓名{学号}→{姓名}。

为了从函数依赖集F中寻找蕴含的函数依赖，比如已知函数依赖集F以及X→YX\to YX→Y，问X→YX \to YX→Y是否为F所蕴含，我们引入一套推理规则，即Armstrong公理系统：

设U为属性集总体，F是U上的一组函数依赖，于是有关系模式R<U,F>，对于R<U,F>有如下推理规则：

1. 自反律 ：若Y⊆X⊆UY\subseteq X \subseteq UY⊆X⊆U，则X→YX\to YX→Y为F所蕴含
2. 增广率：若X→YX\to YX→Y为F所蕴含，且Z⊆UZ\subseteq UZ⊆U，则X∪Z→Y∪ZX\cup Z\to Y \cup ZX∪Z→Y∪Z为F所蕴含
3. 传递率：若X→YX\to YX→Y及Y→ZY \to ZY→Z为F锁蕴含，则X→ZX\to ZX→Z为F所蕴含

注意：由自反律得出的函数依赖均是平凡的函数依赖，因为Y⊆XY\subseteq XY⊆X.

总结

本文我们总结学习了数据库中的关系数据库理论，由于本人太菜，文中可能会出现错误，如有读者发现，请及时联系我修改，不胜感谢。