机器学习之--梯度下降算法
2018-03-05 15:05
435 查看
貌似机器学习最绕不过去的算法,是梯度下降算法。这里专门捋一下。
因为高等数学都忘光了,先从导数/偏倒数/方向导数,慢慢推出梯度吧。
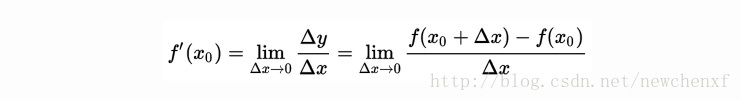
用图可表示为
直白的来说,导数代表了在自变量变化趋于无穷小的时候,函数值的变化与自变量变化的比值代表了导数,几何意义有该点的切线。物理意义有该时刻的(瞬时)变化率…
注意在一元函数中,只有一个自变量变动,也就是说只存在一个方向的变化率,这也就是为什么一元函数没有偏导数的原因。
而我们所说的偏导数就是指的是多元函数沿坐标轴的变化率:
fx(x,y)fx(x,y)指的是函数在y方向不变,函数值沿着x轴方向的变化率
fy(x,y)fy(x,y)指的是函数在x方向不变,函数值沿着y轴方向的变化率
对应的图像形象表达如下:
可能到这里,读者就已经发现偏导数的局限性了,原来我们学到的偏导数指的是多元函数沿坐标轴的变化率,但是我们往往很多时候要考虑多元函数沿任意方向的变化率,那么就引出了方向导数。
山坡图如下:

假设山坡表示为z=f(x,y)z=f(x,y),你应该已经会做主要俩个方向的斜率:
y方向的斜率可以对y偏微分得到。同样的,x方向的斜率也可以对x偏微分得到。
那么我们可以使用这俩个偏微分来求出任何方向的斜率(类似于一个平面的所有向量可以用俩个基向量来表示一样)
现在我们有这个需求,想求出u方向的斜率怎么办?假设z=f(x,y)z=f(x,y)为一个曲面,p(x0,y0)p(x0,y0)为函数定义域中一个点,单位向量可表示为u=cosθi+sinθju=cosθi+sinθj,其中θθ是此向量与x轴正向夹角.单位向量u可以表示对任何方向导数的方向.如下图:
那么我们来考虑如何求出,曲面沿着uu 方向的斜率,可以类比于前面导数定义,得出如下:
设f(x,y)f(x,y)为一个二元函数,u=cosθi+sinθju=cosθi+sinθj为一个单位向量,如果下列的极限值存在
limt→0f(x0+tcosθ,y0+tsinθ)−f(x0,y0)tlimt→0f(x0+tcosθ,y0+tsinθ)−f(x0,y0)t
此方向导数记为DufDuf
则称这个极限值是ff沿着uu方向的方向导数,那么随着θθ 的不同,我们可以求出任意方向的方向导数。这也表明了方向导数的用处,是为了给我们考虑函数对任意方向的变化率.
在求方向导数的时候,除了用上面的定义法求之外,我们还可以用偏微分来简化我们的计算.
表达式是:
Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθDuf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ
(至于为什么成立,很多资料有,不是这里讨论的重点,其实很好理解,θθ为0,就是x轴方向,偏导数不就是fx(x,y)fx(x,y) 嘛)
那么一个平面上无数个方向,函数沿哪个方向变化率最大呢?
目前我不管梯度的事,我先把表达式写出来:
Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθDuf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ
设有这样两个向量:A=(fx(x,y),fy(x,y)),I=(cosθ,sinθ)A=(fx(x,y),fy(x,y)),I=(cosθ,sinθ)
那么我们可以得到:
Duf(x,y)=A∙I=|A|∗|I|cosαDuf(x,y)=A∙I=|A|∗|I|cosα (向量的点乘的基本公式。αα 为向量A与向量I之间的夹角)
那么此时如果Duf(x,y)Duf(x,y)要取得最大值,也就是当αα为0度的时候,也就是向量II(这个方向是一直在变,在寻找一个函数变化最快的方向)与向量AA(这个方向当点固定下来的时候,它就是固定的)平行的时候,方向导数最大。方向导数最大,也就是单位步伐,函数值朝这个反向变化最快。
好了,现在我们已经找到函数值变化最快的方向了,这个方向就是和AA向量相同的方向。那么此时我把AA向量命名为梯度(当一个点确定后,梯度方向是确定的),也就是说明了为什么梯度方向是函数变化率最大的方向了!!!(因为本来就是把这个函数变化最大的方向命名为梯度)
梯度是一个向量,表示某一函数在该点处的方向导数沿着该方向(向量)取得最大值。(导数是一个值)
梯度所指的方向就是函数增长最快的方向(负梯度则指向函数下降最快的方向)。
假设二元函数在平面区域D上具有一阶连续偏导数,则对于每一个点P(x,y)P(x,y)都可定义:
向量 A=(fx(x,y),fy(x,y))A=(fx(x,y),fy(x,y)),该向量就称为函数在点P(x,y)P(x,y)的梯度。
函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
假设有一堆根据衣着判定男女的数据(training set),(x1,x2x1,x2)代鞋码和裤头码的数据,x1x1是鞋码,x2x2是裤头码,y是类标号,y=1表示这条数据是男生,y=-1表示这条数据是女生。我们希望能学习出一个函数f(x)f(x),使得f(x)f(x)能够尽可能准确地描述这些数据,如果能求出这个f(x)f(x),那么任给一组数据,就能预测出这人是男生还是女生。
那么f(x)f(x)长什么样?它的形式需要我们来指定,算法只帮我们训练出其中的参数。为了方便讲解,我设f(x)f(x)为下面的形式,也就是一个线性的函数(一般来说,非线性的要比线性的函数的拟合能力要强,这里暂不讨论线性与非线性的问题):
f(x)=θ1x1+θ2x2+θ3f(x)=θ1x1+θ2x2+θ3
我们希望f(x)f(x)能够尽可能准确地描述training set中的样本,但毕竟是猜的,不可能百分百准确,肯定或多或少会有误差。于是对于一个training set,总的误差函数(也称为损失函数)(cost function)可以定义如下:
L(θ)=12∑ni=1[f(Xi)−Yi]2L(θ)=12∑i=1n[f(Xi)−Yi]2
其中Xi=(x1,x2)Xi=(x1,x2)表示第 i 个样本,YiYi表示第 i 个样本对应的类标号(值为1或-1)。
现在的目标是,找到最优参数(θ1,θ2,θ3)(θ1,θ2,θ3),使得函数 L(θ)L(θ) 取得最小值。因为损失最小,代表模拟出的函数 f(x)f(x) 越准确。
回忆上文的结论:
梯度所指的方向就是函数增长最快的方向(负梯度则指向函数下降最快的方向)。
我们先随机取一个参数值(θ1,θ2,θ3)(θ1,θ2,θ3),然后沿着负梯度的方向调整参数(注意在cost function中,自变量是参数,而不是X,X是已知的样本数据),就可以使我们的损失函数下降得最快,直到无法再降,就是最小值,那时候的参数,就是我们要的参数。
既然是调整参数,那肯定要对他们求导了。
参数(θ1,θ2,θ3)(θ1,θ2,θ3)的偏导数:
∂L∂θ1=∑ni=1xi1(f(Xi)−Yi)∂L∂θ1=∑i=1nx1i(f(Xi)−Yi)
∂L∂θ2=∑ni=1xi2(f(Xi)−Yi)∂L∂θ2=∑i=1nx2i(f(Xi)−Yi)
∂L∂θ3=∑ni=1xi3(f(Xi)−Yi)∂L∂θ3=∑i=1nx3i(f(Xi)−Yi)
可能直接看到这个有点懵逼,没事,推导一下。
L(θ)=12∑ni=1[f(Xi)−Yi]2L(θ)=12∑i=1n[f(Xi)−Yi]2
=12∑ni=1[(θ1x1+θ2x2+θ3)−Yi]2=12∑i=1n[(θ1x1+θ2x2+θ3)−Yi]2
既然是对θ1θ1求偏导,那其他值就相当于常数。且假设T=θ2x2+θ3−YiT=θ2x2+θ3−Yi是一个常数。
L(θ)=12∑ni=1[θ1x1+T]2L(θ)=12∑i=1n[θ1x1+T]2
=12∑ni=1(θ1)2(x1)2+2(θ1)(x1)T+T2=12∑i=1n(θ1)2(x1)2+2(θ1)(x1)T+T2
对θ1θ1求偏导
∂L∂θ1=12∑ni=1[2(θ1)(x1)2+2(x1)T]∂L∂θ1=12∑i=1n[2(θ1)(x1)2+2(x1)T]
=∑ni=1(x1)[θ1x1+T]=∑i=1n(x1)[θ1x1+T]
因为f(Xi)−Yi=θ1x1+Tf(Xi)−Yi=θ1x1+T
故而
∂L∂θ1=∑ni=1x1(f(Xi)−Yi)∂L∂θ1=∑i=1nx1(f(Xi)−Yi)
有严格来说,x1x1是样本数据,根据 i 变化,所以加个上标比较准确。于是公式如下:
∂L∂θ1=∑ni=1xi1(f(Xi)−Yi)∂L∂θ1=∑i=1nx1i(f(Xi)−Yi)
好了,偏导都知道怎么求了,如上文所说,我们先随机取一组参数值,接下来让参数沿着负梯度方向走,也就是每个分量沿着对应的梯度反方向的分量走,因此参数在每次迭代的更新规则如下:
θ1new=θ1−η⋅∂L∂θ1θ1new=θ1−η⋅∂L∂θ1
θ2new=θ2−η⋅∂L∂θ2θ2new=θ2−η⋅∂L∂θ2
θ3new=θ3−η⋅∂L∂θ3θ3new=θ3−η⋅∂L∂θ3
ηη是学习率,一般取值为0到1之间,它可以控制参数每步调整的大小,太大的话,有可能走到临近极佳点时,下一步就跨过去了,这样就不收敛了,走得太慢的话,会迭代很多次才收敛。
ps: 网上总是说,大部分人做机器学习,都是调参工程师,说的一个参,就是这个ηη,哈哈^^
anyway,经过多次迭代之后,我们就得到了的(θ1,θ2,θ3)(θ1,θ2,θ3)最优值,也就是在这些个参数下,f(x)f(x)对于training set的样本的识别误差最小。这样,我们就训练出了函数f(x)f(x)(机器学习领域,可称这个函数为模型),以后随意输入一组样本(x1,x2)(x1,x2), 我们都可以直接输出结果。
gradient descent 梯度下降算法
1. 什么是梯度
有知乎大神已经解释的很不错,这里转载并稍作修改,加上自己的看法。先给出链接,毕竟转载要说明出处嘛。为什么梯度反方向是函数值局部下降最快的方向?因为高等数学都忘光了,先从导数/偏倒数/方向导数,慢慢推出梯度吧。
1.1 导数
导数的几何意义可能很多人都比较熟悉: 当函数定义域和取值都在实数域中的时候,导数可以表示函数曲线上的切线斜率。 除了切线的斜率,导数还表示函数在该点的变化率。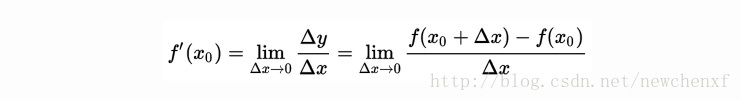
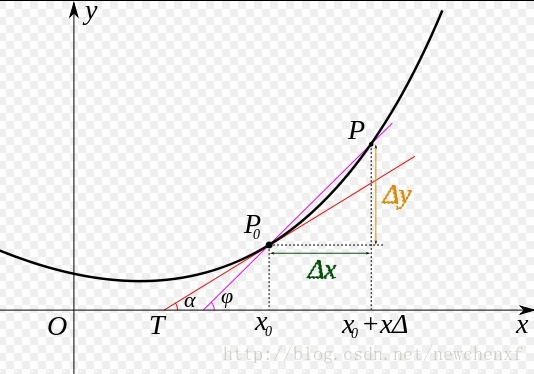
用图可表示为

直白的来说,导数代表了在自变量变化趋于无穷小的时候,函数值的变化与自变量变化的比值代表了导数,几何意义有该点的切线。物理意义有该时刻的(瞬时)变化率…
注意在一元函数中,只有一个自变量变动,也就是说只存在一个方向的变化率,这也就是为什么一元函数没有偏导数的原因。
1.2 偏导数
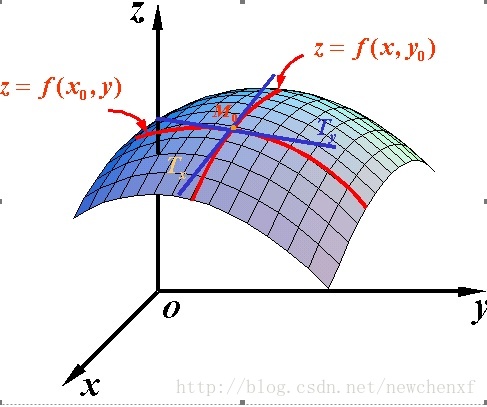
既然谈到偏导数,那就至少涉及到两个自变量,以两个自变量为例,z=f(x,y) 。从导数到偏导数,也就是从曲线来到了曲面. 曲线上的一点,其切线只有一条。但是曲面的一点,切线有无数条。而我们所说的偏导数就是指的是多元函数沿坐标轴的变化率:
fx(x,y)fx(x,y)指的是函数在y方向不变,函数值沿着x轴方向的变化率
fy(x,y)fy(x,y)指的是函数在x方向不变,函数值沿着y轴方向的变化率
对应的图像形象表达如下:

可能到这里,读者就已经发现偏导数的局限性了,原来我们学到的偏导数指的是多元函数沿坐标轴的变化率,但是我们往往很多时候要考虑多元函数沿任意方向的变化率,那么就引出了方向导数。
1.3 方向导数
假设你站在山坡上,想知道山坡的坡度(倾斜度)山坡图如下:

假设山坡表示为z=f(x,y)z=f(x,y),你应该已经会做主要俩个方向的斜率:
y方向的斜率可以对y偏微分得到。同样的,x方向的斜率也可以对x偏微分得到。
那么我们可以使用这俩个偏微分来求出任何方向的斜率(类似于一个平面的所有向量可以用俩个基向量来表示一样)
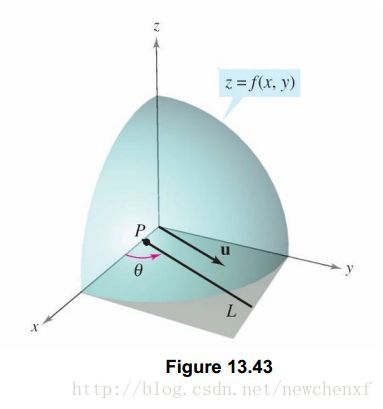
现在我们有这个需求,想求出u方向的斜率怎么办?假设z=f(x,y)z=f(x,y)为一个曲面,p(x0,y0)p(x0,y0)为函数定义域中一个点,单位向量可表示为u=cosθi+sinθju=cosθi+sinθj,其中θθ是此向量与x轴正向夹角.单位向量u可以表示对任何方向导数的方向.如下图:

那么我们来考虑如何求出,曲面沿着uu 方向的斜率,可以类比于前面导数定义,得出如下:
设f(x,y)f(x,y)为一个二元函数,u=cosθi+sinθju=cosθi+sinθj为一个单位向量,如果下列的极限值存在
limt→0f(x0+tcosθ,y0+tsinθ)−f(x0,y0)tlimt→0f(x0+tcosθ,y0+tsinθ)−f(x0,y0)t
此方向导数记为DufDuf
则称这个极限值是ff沿着uu方向的方向导数,那么随着θθ 的不同,我们可以求出任意方向的方向导数。这也表明了方向导数的用处,是为了给我们考虑函数对任意方向的变化率.
在求方向导数的时候,除了用上面的定义法求之外,我们还可以用偏微分来简化我们的计算.
表达式是:
Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθDuf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ
(至于为什么成立,很多资料有,不是这里讨论的重点,其实很好理解,θθ为0,就是x轴方向,偏导数不就是fx(x,y)fx(x,y) 嘛)
那么一个平面上无数个方向,函数沿哪个方向变化率最大呢?
目前我不管梯度的事,我先把表达式写出来:
Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθDuf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ
设有这样两个向量:A=(fx(x,y),fy(x,y)),I=(cosθ,sinθ)A=(fx(x,y),fy(x,y)),I=(cosθ,sinθ)
那么我们可以得到:
Duf(x,y)=A∙I=|A|∗|I|cosαDuf(x,y)=A∙I=|A|∗|I|cosα (向量的点乘的基本公式。αα 为向量A与向量I之间的夹角)
那么此时如果Duf(x,y)Duf(x,y)要取得最大值,也就是当αα为0度的时候,也就是向量II(这个方向是一直在变,在寻找一个函数变化最快的方向)与向量AA(这个方向当点固定下来的时候,它就是固定的)平行的时候,方向导数最大。方向导数最大,也就是单位步伐,函数值朝这个反向变化最快。
好了,现在我们已经找到函数值变化最快的方向了,这个方向就是和AA向量相同的方向。那么此时我把AA向量命名为梯度(当一个点确定后,梯度方向是确定的),也就是说明了为什么梯度方向是函数变化率最大的方向了!!!(因为本来就是把这个函数变化最大的方向命名为梯度)
1.4 梯度
由上面,总结一下梯度的结论。梯度是一个向量,表示某一函数在该点处的方向导数沿着该方向(向量)取得最大值。(导数是一个值)
梯度所指的方向就是函数增长最快的方向(负梯度则指向函数下降最快的方向)。
假设二元函数在平面区域D上具有一阶连续偏导数,则对于每一个点P(x,y)P(x,y)都可定义:
向量 A=(fx(x,y),fy(x,y))A=(fx(x,y),fy(x,y)),该向量就称为函数在点P(x,y)P(x,y)的梯度。
函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
2. 梯度下降算法
这里就从一个不成熟但能用的例子开始讲。假设有一堆根据衣着判定男女的数据(training set),(x1,x2x1,x2)代鞋码和裤头码的数据,x1x1是鞋码,x2x2是裤头码,y是类标号,y=1表示这条数据是男生,y=-1表示这条数据是女生。我们希望能学习出一个函数f(x)f(x),使得f(x)f(x)能够尽可能准确地描述这些数据,如果能求出这个f(x)f(x),那么任给一组数据,就能预测出这人是男生还是女生。
那么f(x)f(x)长什么样?它的形式需要我们来指定,算法只帮我们训练出其中的参数。为了方便讲解,我设f(x)f(x)为下面的形式,也就是一个线性的函数(一般来说,非线性的要比线性的函数的拟合能力要强,这里暂不讨论线性与非线性的问题):
f(x)=θ1x1+θ2x2+θ3f(x)=θ1x1+θ2x2+θ3
我们希望f(x)f(x)能够尽可能准确地描述training set中的样本,但毕竟是猜的,不可能百分百准确,肯定或多或少会有误差。于是对于一个training set,总的误差函数(也称为损失函数)(cost function)可以定义如下:
L(θ)=12∑ni=1[f(Xi)−Yi]2L(θ)=12∑i=1n[f(Xi)−Yi]2
其中Xi=(x1,x2)Xi=(x1,x2)表示第 i 个样本,YiYi表示第 i 个样本对应的类标号(值为1或-1)。
现在的目标是,找到最优参数(θ1,θ2,θ3)(θ1,θ2,θ3),使得函数 L(θ)L(θ) 取得最小值。因为损失最小,代表模拟出的函数 f(x)f(x) 越准确。
回忆上文的结论:
梯度所指的方向就是函数增长最快的方向(负梯度则指向函数下降最快的方向)。
我们先随机取一个参数值(θ1,θ2,θ3)(θ1,θ2,θ3),然后沿着负梯度的方向调整参数(注意在cost function中,自变量是参数,而不是X,X是已知的样本数据),就可以使我们的损失函数下降得最快,直到无法再降,就是最小值,那时候的参数,就是我们要的参数。
既然是调整参数,那肯定要对他们求导了。
参数(θ1,θ2,θ3)(θ1,θ2,θ3)的偏导数:
∂L∂θ1=∑ni=1xi1(f(Xi)−Yi)∂L∂θ1=∑i=1nx1i(f(Xi)−Yi)
∂L∂θ2=∑ni=1xi2(f(Xi)−Yi)∂L∂θ2=∑i=1nx2i(f(Xi)−Yi)
∂L∂θ3=∑ni=1xi3(f(Xi)−Yi)∂L∂θ3=∑i=1nx3i(f(Xi)−Yi)
可能直接看到这个有点懵逼,没事,推导一下。
L(θ)=12∑ni=1[f(Xi)−Yi]2L(θ)=12∑i=1n[f(Xi)−Yi]2
=12∑ni=1[(θ1x1+θ2x2+θ3)−Yi]2=12∑i=1n[(θ1x1+θ2x2+θ3)−Yi]2
既然是对θ1θ1求偏导,那其他值就相当于常数。且假设T=θ2x2+θ3−YiT=θ2x2+θ3−Yi是一个常数。
L(θ)=12∑ni=1[θ1x1+T]2L(θ)=12∑i=1n[θ1x1+T]2
=12∑ni=1(θ1)2(x1)2+2(θ1)(x1)T+T2=12∑i=1n(θ1)2(x1)2+2(θ1)(x1)T+T2
对θ1θ1求偏导
∂L∂θ1=12∑ni=1[2(θ1)(x1)2+2(x1)T]∂L∂θ1=12∑i=1n[2(θ1)(x1)2+2(x1)T]
=∑ni=1(x1)[θ1x1+T]=∑i=1n(x1)[θ1x1+T]
因为f(Xi)−Yi=θ1x1+Tf(Xi)−Yi=θ1x1+T
故而
∂L∂θ1=∑ni=1x1(f(Xi)−Yi)∂L∂θ1=∑i=1nx1(f(Xi)−Yi)
有严格来说,x1x1是样本数据,根据 i 变化,所以加个上标比较准确。于是公式如下:
∂L∂θ1=∑ni=1xi1(f(Xi)−Yi)∂L∂θ1=∑i=1nx1i(f(Xi)−Yi)
好了,偏导都知道怎么求了,如上文所说,我们先随机取一组参数值,接下来让参数沿着负梯度方向走,也就是每个分量沿着对应的梯度反方向的分量走,因此参数在每次迭代的更新规则如下:
θ1new=θ1−η⋅∂L∂θ1θ1new=θ1−η⋅∂L∂θ1
θ2new=θ2−η⋅∂L∂θ2θ2new=θ2−η⋅∂L∂θ2
θ3new=θ3−η⋅∂L∂θ3θ3new=θ3−η⋅∂L∂θ3
ηη是学习率,一般取值为0到1之间,它可以控制参数每步调整的大小,太大的话,有可能走到临近极佳点时,下一步就跨过去了,这样就不收敛了,走得太慢的话,会迭代很多次才收敛。
ps: 网上总是说,大部分人做机器学习,都是调参工程师,说的一个参,就是这个ηη,哈哈^^
anyway,经过多次迭代之后,我们就得到了的(θ1,θ2,θ3)(θ1,θ2,θ3)最优值,也就是在这些个参数下,f(x)f(x)对于training set的样本的识别误差最小。这样,我们就训练出了函数f(x)f(x)(机器学习领域,可称这个函数为模型),以后随意输入一组样本(x1,x2)(x1,x2), 我们都可以直接输出结果。
参考
如何直观形象的理解方向导数与梯度以及它们之间的关系?gradient descent 梯度下降算法
相关文章推荐
- 机器学习——梯度下降算法
- 机器学习笔记(三) 线性回归及梯度下降算法
- coursera《机器学习》吴恩达-week1-03 梯度下降算法
- 【机器学习】(2):梯度下降算法
- 机器学习-梯度下降算法
- 【机器学习】对梯度下降算法的进一步理解
- 斯坦福机器学习: 网易公开课系列笔记(二)——线性回归、梯度下降算法和最小二乘公式
- 梯度下降算法推导(机器学习系列-1)
- 斯坦福《机器学习》课程算法matlab实现之梯度下降算法——直线回归(一)
- 机器学习之梯度下降算法Gradient Descent
- 机器学习1_线性回归梯度下降算法
- 机器学习——梯度下降算法
- 机器学习入门(11)--多特征量梯度下降算法
- 机器学习1_线性回归梯度下降算法
- 一文清晰讲解机器学习中梯度下降算法(包括其变式算法)
- 一文清晰讲解机器学习中梯度下降算法(包括其变式算法)
- 机器学习1_线性回归梯度下降算法
- 【机器学习 基本概念】随机梯度下降算法与批量梯度下降算法
- 机器学习1_线性回归梯度下降算法
- 机器学习-梯度下降算法
