How to use Multinomial and Ordinal Logistic Regression in R ?

以下内容转自https://www.analyticsvidhya.com/blog/2016/02/multinomial-ordinal-logistic-regression/

How to use Multinomial and Ordinal Logistic Regression in R ?

Introduction

Most of us have limited knowledge of regression. Of which, linear and logistic regression are our favorite ones. As an interesting fact, regression has extended capabilities to deal with different types of variables. Do you know, regression has provisions for dealing with multi-level dependent variables too? I’m sure, you didn’t. Neither did I. Until I was pushed to explore this aspect of Regression.

For multi-level dependent variables, there are many machine learning algorithms which can do the job for you; such as naive bayes, decision tree, random forest etc. For starters, these algorithm can be a bit difficult to understand. But, if you very well understand logistic regression, mastering this new aspect of regression should be easy for you!

In this article, I’ve explained the method of using multinomial and ordinal regression. Also, for practical purpose, I’ve demonstrated this algorithm in a step wise fashion in R. This article draws inspiration from a detailed article here . I have added my own take on it.

Note: This article is best suited for R users having prior knowledge of logistic regression. However, if you use python, you can still get a overall understanding of this regression method.

What is Multinomial Regression ?

Multinomial Logistic Regression (MLR) is a form of linear regression analysis conducted when the dependent variable is nominal with more than two levels. It is used to describe data and to explain the relationship between one dependent nominal variable and one or more continuous-level (interval or ratio scale) independent variables. You can understand nominal variable as, a variable which has no intrinsic ordering.

For example: Types of Forests: ‘Evergreen Forest’, ‘Deciduous Forest’, ‘Rain Forest’. As you see, there is no intrinsic order in them, but each forest represent a unique category. In other words, multinomial regression is an extension of logistic regression, which analyzes dichotomous (binary) dependents.

How does Multinomial Regression works ?

The multinomial logistic regression estimates a separate binary logistic regression model for each dummy variables. The result is M-1 binary logistic regression models. Each model conveys the effect of predictors on the probability of success in that category, in comparison to the reference category.

Each model has its own intercept and regression coefficients—the predictors can affect each category differently. Let’s compare this part with our classics – Linear and Logistic Regression.

Standard linear regression requires the dependent variable to be of continuous-level (interval or ratio) scale. However, logistic regression jumps the gap by assuming that the dependent variable is a stochastic event. And the dependent variable describes the outcome of this stochastic event with a density function (a function of cumulated probabili
4000
ties ranging from 0 to 1).

Statisticians then argue one event happens if the probability is less than 0.5 and the opposite event happens when probability is greater than 0.5.

Now we know that MLR extends the binary logistic model to a model with numerous categories(in dependent variable). However, it has one limitation. The category to which an outcome belongs to, does not assume any order in it. For example, if we have N categories, all have an equal probability. In reality, we come across problems where categories have a natural order.

So, what to do when we have a natural order in categories of dependent variables ? In such situation, Ordinal Regression comes to our rescue.

What is Ordinal Regression ?

Ordinal Regression ( also known as Ordinal Logistic Regression) is another extension of binomial logistics regression. Ordinal regression is used to predict the dependent variable with ‘ordered’ multiple categories and independent variables. In other words, it is used to facilitate the interaction of dependent variables (having multiple ordered levels) with one or more independent variables.

For example: Let us assume a survey is done. We asked a question to respondent where their answer lies between agree or disagree. The responses thus collected didn’t help us to generalize well. Later, we added levels to our responses such as Strongly Disagree, Disagree, Agree, Strongly Agree.

This helped us to observe a natural order in the categories. For our regression model to be realistic, we must appreciate this order instead of being naive to it, as in the case of MLR. Ordinal Logistic Regression addresses this fact. Ordinal means order of the categories.

Examples

Before we perform these algorithm in R, let’s ensure that we have gained a concrete understanding using the cases below:

Case 1 (Multinomial Regression)

The modeling of program choices made by high school students can be done using Multinomial logit. The program choices are general program, vocational program and academic program. Their choice can be modeled using their writing score and their social economic status.

Based on a variety of attributes such as social status, channel type, awards and accolades received by the students, gender, economic status and how well they are able to read and write in the subjects given, the choice on the type of program can be predicted. Choice of programs with multiple levels (unordered) is the dependent variable. This case is suited for using Multinomial Logistic Regression technique.

Case 2 (Ordinal Regression)

A study looks at factors which influence the decision of whether to apply to graduate school. College juniors are asked if they are unlikely, somewhat likely, or very likely to apply to graduate school. Hence, our outcome variable has three categories i.e. unlikely, somewhat likely and very likely.

Data on parental educational status, class of institution (private or state run), current GPA are also collected. The researchers have reason to believe that the “distances” between these three points are not equal. For example, the “distance” between “unlikely” and “somewhat likely” may be shorter than the distance between “somewhat likely” and “very likely”. In such case, we’ll use Ordinal Regression.

Multinomial Logistic Regression (MLR) in R

Read the file

library("foreign")
ml <- read.dta("http://www.ats.ucla.edu/stat/data/hsbdemo.dta")

Re-leveling data

head(ml)

##    id female    ses schtyp     prog read write math science socst
## 1  45 female    low public vocation   34    35   41      29    26
## 2 108   male middle public  general   34    33   41      36    36
## 3  15   male   high public vocation   39    39   44      26    42
## 4  67   male    low public vocation   37    37   42      33    32
## 5 153   male middle public vocation   39    31   40      39    51
## 6  51 female   high public  general   42    36   42      31    39
##         honors awards cid
## 1 not enrolled      0   1
## 2 not enrolled      0   1
## 3 not enrolled      0   1
## 4 not enrolled      0   1
## 5 not enrolled      0   1
## 6 not enrolled      0   1

ml$prog2 <- relevel(ml$prog, ref = "academic")

Now we’ll execute a multinomial regression with two independent variable.

> library("nnet")
> test <- multinom(prog2 ~ ses + write, data = ml)

## # weights:  15 (8 variable)
## initial  value 219.722458
## iter  10 value 179.982880
## final  value 179.981726
## converged

summary(test)

## Call:
## multinom(formula = prog2 ~ ses + write, data = ml)
##
## Coefficients:
##          (Intercept)  sesmiddle    seshigh      write
## general     2.852198 -0.5332810 -1.1628226 -0.0579287
## vocation    5.218260  0.2913859 -0.9826649 -0.1136037
##
## Std. Errors:
##          (Intercept) sesmiddle   seshigh      write
## general     1.166441 0.4437323 0.5142196 0.02141097
## vocation    1.163552 0.4763739 0.5955665 0.02221996
##
## Residual Deviance: 359.9635
## AIC: 375.9635

Interpretation

Model execution output shows some iteration history and includes the final negative log-likelihood 179.981726. This value is multiplied by two as shown in the model summary as the Residual Deviance.

The summary output has a block of coefficients and another block of standard errors. Each blocks has one row of values corresponding to one model equation. In the block of coefficients, we see that the first row is being compared to prog = “general” to our baseline prog = “academic” and the second row to prog = “vocation” to our baseline prog = “academic”.

A one-unit increase in write decreases the log odds of being in general program vs. academic program by 0.0579

A one-unit increase in write decreases the log odds of being in vocation program vs. academic program by 0.1136

The log odds of being in general program than in academic program will decrease by 1.163 if moving from ses=”low” to ses=”high”.

On the other hand, Log odds of being in general program than in academic program will decrease by 0.5332 if moving from ses=”low” to ses=”middle”

The log odds of being in vocation program vs. in academic program will decrease by 0.983 if moving from ses=”low” to ses=”high”

The log odds of being in vocation program vs. in academic program will increase by 0.291 if moving from ses=”low” to ses=”middle”

Now we’ll calculate Z score and p-Value for the variables in the model.

z <- summary(test)$coefficients/summary(test)$standard.errors
z

##          (Intercept)  sesmiddle   seshigh     write
## general     2.445214 -1.2018081 -2.261334 -2.705562
## vocation    4.484769  0.6116747 -1.649967 -5.112689

> p <- (1 - pnorm(abs(z), 0, 1))*2
> p

##           (Intercept) sesmiddle    seshigh        write
## general  0.0144766100 0.2294379 0.02373856 6.818902e-03
## vocation 0.0000072993 0.5407530 0.09894976 3.176045e-07

exp(coef(test))

##          (Intercept) sesmiddle   seshigh     write
## general     17.32582 0.5866769 0.3126026 0.9437172
## vocation   184.61262 1.3382809 0.3743123 0.8926116

The p-Value tells us that ses variables are not significant. Now we’ll explore the entire data set, and analyze if we can remove any variables which do not add to model performance.

names(ml)

##  [1] "id"      "female"  "ses"     "schtyp"  "prog"    "read"    "write"
##  [8] "math"    "science" "socst"   "honors"  "awards"  "cid"     "prog2"

levels(ml$female)

## [1] "male"   "female"

levels(ml$ses)

## [1] "low"    "middle" "high"

levels(ml$schtyp)

## [1] "public"  "private"

levels(ml$honors)

## [1] "not enrolled" "enrolled"

Let’s now build a multinomial model on the entire data set after removing id and prog variables.

test <- multinom(prog2 ~ ., data = ml[,-c(1,5,13)])

## # weights:  39 (24 variable)
## initial  value 219.722458
## iter  10 value 178.757016
## iter  20 value 155.866327
## iter  30 value 154.365307
## final  value 154.365305
## converged

summary(test)

## Call:
## multinom(formula = prog2 ~ ., data = ml[, -c(1, 5, 13)])
##
## Coefficients:
##          (Intercept) femalefemale  sesmiddle       seshigh schtypprivate
## general     5.692368    0.1547445 -0.2809824 -0.9632924107    -0.5872049
## vocation    9.839107    0.4076641  1.2246933  0.0008659972    -1.9089941
##                 read       write       math    science       socst
## general  -0.04421300 -0.05434029 -0.1001477 0.10397170 -0.02486526
## vocation -0.04124332 -0.05149742 -0.1209839 0.06341246 -0.07012002
##          honorsenrolled      awards
## general      -0.5963679  0.26104317
## vocation      1.0986972 -0.08573852
##
## Std. Errors:
##          (Intercept) femalefemale sesmiddle   seshigh schtypprivate
## general     2.385383    0.4514339 0.5224132 0.5934146     0.5597181
## vocation    2.566895    0.4993567 0.5764471 0.6885407     0.8313621
##                read      write       math    science      socst
12eef

## general  0.03076523 0.05109711 0.03514069 0.03153073 0.02697888
## vocation 0.03451435 0.05358824 0.03902319 0.03252487 0.02912126
##          honorsenrolled    awards
## general       0.8708913 0.2969302
## vocation      0.9798571 0.3708768
##
## Residual Deviance: 308.7306
## AIC: 356.7306

Let’s check for fitted values now.

head(fitted(test))

##     academic   general  vocation
## 1 0.08952937 0.1811189 0.7293518
## 2 0.05219222 0.1229310 0.8248768
## 3 0.54704495 0.0849831 0.3679719
## 4 0.17103536 0.2750466 0.5539180
## 5 0.10014015 0.2191946 0.6806652
## 6 0.27287474 0.1129348 0.6141905

Once we have build the model, we’ll use it for prediction. Let us create a new data set with different permutation and combinations.

expanded=expand.grid(female=c("female", "male", "male", "male"),
ses=c("low","low","middle", "high"),
schtyp=c("public", "public", "private", "private"),
read=c(20,50,60,70),
write=c(23,45,55,65),
math=c(30,46,76,54),
science=c(25,45,68,51),
socst=c(30, 35, 67, 61),
honors=c("not enrolled", "not enrolled", "enrolled","not enrolled"),
awards=c(0,0,3,0,6) )

head(expanded)

##   female ses schtyp read write math science socst       honors awards
## 1 female low public   20    23   30      25    30 not enrolled      0
## 2   male low public   20    23   30      25    30 not enrolled      0
## 3   male low public   20    23   30      25    30 not enrolled      0
## 4   male low public   20    23   30      25    30 not enrolled      0
## 5 female low public   20    23   30      25    30 not enrolled      0
## 6   male low public   20    23   30      25    30 not enrolled      0

predicted=predict(test,expanded,type="probs")
head(predicted)

##     academic   general  vocation
## 1 0.01357216 0.1759060 0.8105219
## 2 0.01929452 0.2142205 0.7664850
## 3 0.01929452 0.2142205 0.7664850
## 4 0.01929452 0.2142205 0.7664850
## 5 0.01357216 0.1759060 0.8105219
## 6 0.01929452 0.2142205 0.7664850

Now, we’ll calculate the prediction values. The parameter type=”probs”, specifies our interest in probabilities. In order to plot predicted probabilities for intuitive understanding, we add predicted probability values to data.

bpp=cbind(expanded, predicted)

Now we’ll calculate the mean probabilities within each level of ses.

by(bpp[,4:7], bpp$ses, colMeans)

## bpp$ses: low
##    read   write    math science
##   50.00   47.00   51.50   47.25
## --------------------------------------------------------
## bpp$ses: middle
##    read   write    math science
##   50.00   47.00   51.50   47.25
## --------------------------------------------------------
## bpp$ses: high
##    read   write    math science
##   50.00   47.00   51.50   47.25

I’ve used the melt() function from ‘reshape2’ package. It “melts” data with the purpose of each row being a unique id-variable combination.

library("reshape2")

## Warning: package 'reshape2' was built under R version 3.1.3

bpp2 = melt (bpp,id.vars=c("female", "ses","schtyp", "read","write","math","science","socst","honors", "awards"),value.name="probablity")

head(bpp2)

##   female ses schtyp read write math science socst       honors awards
## 1 female low public   20    23   30      25    30 not enrolled      0
## 2   male low public   20    23   30      25    30 not enrolled      0
## 3   male low public   20    23   30      25    30 not enrolled      0
## 4   male low public   20    23   30      25    30 not enrolled      0
## 5 female low public   20    23   30      25    30 not enrolled      0
## 6   male low public   20    23   30      25    30 not enrolled      0
##   variable probablity
## 1 academic 0.01357216
## 2 academic 0.01929452
## 3 academic 0.01929452
## 4 academic 0.01929452
## 5 academic 0.01357216
## 6 academic 0.01929452

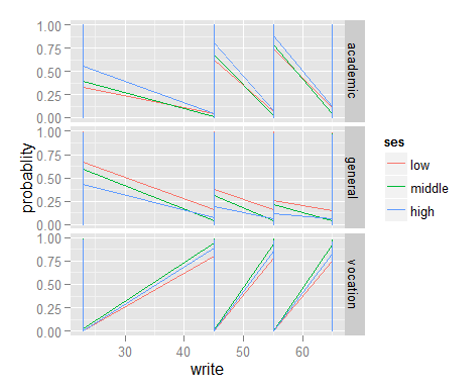
Now, we will be plotting graphs to explore the distribution of dependent variable vs independent variables, using ggplot() function. In ggplot, the first parameter in this function is the data values to be plotted. The second part is where (aes()) binds variables to x and y axis. We tell the plotting function to draw a line using geom_line(). We are differentiating the school type by plotting them in different colors.

> library("ggplot2")

> ggplot(bpp2, aes(x = write, y = probablity, colour = ses)) +
geom_line() + facet_grid(variable ~ ., scales="free")

Till here, we have learnt to use multinomial regression in R. As mentioned above, if you have prior knowledge of logistic regression, interpreting the results wouldn’t be too difficult. Let’s now proceed to understand ordinal regression in R.

Ordinal Logistic Regression (OLR) in R

Below are the steps to perform OLR in R:

Load the Libraries

require(foreign)
require(ggplot2)
require(MASS)
require(Hmisc)
require(reshape2)

Load the data

dat <- read.dta("http://www.ats.ucla.edu/stat/data/ologit.dta")
head(dat)

##             apply pared public  gpa
## 1     very likely     0      0 3.26
## 2 somewhat likely     1      0 3.21
## 3        unlikely     1      1 3.94
## 4 somewhat likely     0      0 2.81
## 5 somewhat likely     0      0 2.53
## 6        unlikely     0      1 2.59

Let’s quickly understand the data.

The data set has a dependent variable known as apply. It has 3 levels namely “unlikely”, “somewhat likely”, and “very likely”, coded in 1, 2, and 3 respectively. 3 being highest and 1 being lowest. This situation is best for using ordinal regression because of presence of ordered categories. Pared (0/1) refers to at least one parent has a graduate degree; public (0/1) refers to the type of undergraduate institute.

For building this model, we will be using the polr command to estimate an ordered logistic regression. Then, we’ll specify Hess=TRUE to let the model output show the observed information matrix from optimization which is used to get standard errors.

m <- polr(apply ~ pared + public + gpa, data = dat, Hess=TRUE)
summary(m)

## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE)
##
## Coefficients:
##           Value Std. Error t value
## pared   1.04769     0.2658  3.9418
## public -0.05879     0.2979 -0.1974
## gpa     0.61594     0.2606  2.3632
##
## Intercepts:
##                             Value   Std. Error t value
## unlikely|somewhat likely     2.2039  0.7795     2.8272
## somewhat likely|very likely  4.2994  0.8043     5.3453
##
## Residual Deviance: 717.0249
## AIC: 727.0249

We see the usual regression output coefficient table including the value of each coefficient, standard errors, t values, estimates for the two intercepts, residual deviance and AIC. AIC is the information criteria. Lesser the better.

Now we’ll calculate some essential metrics such as p-Value, CI, Odds ratio

ctable <- coef(summary(m))

##                                   Value Std. Error    t value
## pared                        1.04769010  0.2657894  3.9418050
## public                      -0.05878572  0.2978614 -0.1973593
## gpa                          0.61594057  0.2606340  2.3632399
## unlikely|somewhat likely     2.20391473  0.7795455  2.8271792
## somewhat likely|very likely  4.29936315  0.8043267  5.3452947

p <- pnorm(abs(ctable[, "t value"]), lower.tail = FALSE) * 2
ctable <- cbind(ctable, "p value" = p)

##                                   Value Std. Error    t value      p value
## pared                        1.04769010  0.2657894  3.9418050 8.087072e-05
## public                      -0.05878572  0.2978614 -0.1973593 8.435464e-01
## gpa                          0.61594057  0.2606340  2.3632399 1.811594e-02
## unlikely|somewhat likely     2.20391473  0.7795455  2.8271792 4.696004e-03
## somewhat likely|very likely  4.29936315  0.8043267  5.3452947 9.027008e-08

# confidence intervals
> ci <- confint(m)

## Waiting for profiling to be done...

##             2.5 %    97.5 %
## pared   0.5281768 1.5721750
## public -0.6522060 0.5191384
## gpa     0.1076202 1.1309148

exp(coef(m))

##     pared    public       gpa
## 2.8510579 0.9429088 1.8513972

## OR and CI

exp(cbind(OR = coef(m), ci))

##               OR     2.5 %   97.5 %
## pared  2.8510579 1.6958376 4.817114
## public 0.9429088 0.5208954 1.680579
## gpa    1.8513972 1.1136247 3.098490

Interpretation

One unit increase in parental education, from 0 (Low) to 1 (High), the odds of “very likely” applying versus “somewhat likely” or “unlikely” applying combined are 2.85 greater .

The odds “very likely” or “somewhat likely” applying versus “unlikely” applying is 2.85 times greater .

For gpa, when a student’s gpa moves 1 unit, the odds of moving from “unlikely” applying to “somewhat likely” or “very likley” applying (or from the lower and middle categories to the high category) are multiplied by 1.85.

Let’s now try to enhance this model to obtain better prediction estimates.

summary(m)

## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE)
##
## Coefficients:
##           Value Std. Error t value
## pared   1.04769     0.2658  3.9418
## public -0.05879     0.2979 -0.1974
## gpa     0.61594     0.2606  2.3632
##
## Intercepts:
##                             Value   Std. Error t value
## unlikely|somewhat likely     2.2039  0.7795     2.8272
## somewhat likely|very likely  4.2994  0.8043     5.3453
##
## Residual Deviance: 717.0249
## AIC: 727.0249

summary(update(m, method = "probit", Hess = TRUE), digits = 3)

## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE,
##     method = "probit")
##
## Coefficients:
##         Value Std. Error t value
## pared  0.5981      0.158  3.7888
## public 0.0102      0.173  0.0588
## gpa    0.3582      0.157  2.2848
##
## Intercepts:
##                             Value Std. Error t value
## unlikely|somewhat likely    1.297 0.468      2.774
## somewhat likely|very likely 2.503 0.477      5.252
##
## Residual Deviance: 717.4951
## AIC: 727.4951

summary(update(m, method = "logistic", Hess = TRUE), digits = 3)

## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE,
##     method = "logistic")
##
## Coefficients:
##          Value Std. Error t value
## pared   1.0477      0.266   3.942
## public -0.0588      0.298  -0.197
## gpa     0.6159      0.261   2.363
##
## Intercepts:
##                             Value  Std. Error t value
## unlikely|somewhat likely     2.204  0.780      2.827
## somewhat likely|very likely  4.299  0.804      5.345
##
## Residual Deviance: 717.0249
## AIC: 727.0249

summary(update(m, method = "cloglog", Hess = TRUE), digits = 3)

## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE,
##     method = "cloglog")
##
## Coefficients:
##        Value Std. Error t value
## pared  0.517      0.161   3.202
## public 0.108      0.168   0.643
## gpa    0.334      0.154   2.168
##
## Intercepts:
##                             Value Std. Error t value
## unlikely|somewhat likely    0.871 0.455      1.912
## somewhat likely|very likely 1.974 0.461      4.287
##
## Residual Deviance: 719.4982
## AIC: 729.4982

Let’s add interaction terms here.

head(predict(m, dat, type = “p”))

##    unlikely somewhat likely very likely
## 1 0.5488310       0.3593310  0.09183798
## 2 0.3055632       0.4759496  0.21848725
## 3 0.2293835       0.4781951  0.29242138
## 4 0.6161224       0.3126888  0.07118879
## 5 0.6560149       0.2833901  0.06059505
## 6 0.6609240       0.2797117  0.05936430

addterm(m, ~.^2, test = "Chisq")

## Single term additions
##
## Model:
## apply ~ pared + public + gpa
##              Df    AIC     LRT Pr(Chi)
## <none>          727.02
## pared:public  1 727.81 1.21714  0.2699
## pared:gpa     1 728.98 0.04745  0.8276
## public:gpa    1 728.60 0.42953  0.5122

m2 <- stepAIC(m, ~.^2)
m2

## Start:  AIC=727.02
## apply ~ pared + public + gpa
##
##                Df    AIC
## - public        1 725.06
## <none>            727.02
## + pared:public  1 727.81
## + public:gpa    1 728.60
## + pared:gpa     1 728.98
## - gpa           1 730.67
## - pared         1 740.60
##
## Step:  AIC=725.06
## apply ~ pared + gpa
##
##             Df    AIC
## <none>         725.06
## + pared:gpa  1 727.02
## + public     1 727.02
## - gpa        1 728.79
## - pared      1 738.60

summary(m2)

## Call:
## polr(formula = apply ~ pared + gpa, data = dat, Hess = TRUE)
##
## Coefficients:
##        Value Std. Error t value
## pared 1.0457     0.2656   3.937
## gpa   0.6042     0.2539   2.379
##
## Intercepts:
##                             Value  Std. Error t value
## unlikely|somewhat likely    2.1763 0.7671     2.8370
## somewhat likely|very likely 4.2716 0.7922     5.3924
##
## Residual Deviance: 717.0638
## AIC: 725.0638

m2$anova

## Stepwise Model Path
## Analysis of Deviance Table
##
## Initial Model:
## apply ~ pared + public + gpa
##
## Final Model:
## apply ~ pared + gpa
##
##
##       Step Df   Deviance Resid. Df Resid. Dev      AIC
## 1                              395   717.0249 727.0249
## 2 - public  1 0.03891634       396   717.0638 725.0638

anova(m, m2)

## Likelihood ratio tests of ordinal regression models
##
## Response: apply
##                  Model Resid. df Resid. Dev   Test    Df   LR stat.
## 1          pared + gpa       396   717.0638
## 2 pared + public + gpa       395   717.0249 1 vs 2     1 0.03891634
##     Pr(Chi)
## 1
## 2 0.8436145

Time to plot this model.

m3 <- update(m, Hess=TRUE)
pr <- profile(m3)
confint(pr)

##             2.5 %    97.5 %
## pared   0.5281772 1.5721695
## public -0.6522008 0.5191415
## gpa     0.1076189 1.1309092

plot(pr)

pairs(pr)

End Notes

I enjoyed writing this article. I’d suggest you to pay attention to interpretation aspect of the model. Coding is relatively easy, but unless you know what’s resulting, you learning will be incomplete.

There are many essential factors such as AIC, Residuals values to determine the effectiveness of the model. If you still struggle to understand them, I’d suggest you to brush your Basics of Logistic Regression. This should help you in understanding this concept better.

In this article, I shared my understanding of using multinomial and ordinal regression in R. These techniques are used when the dependent variable has levels either ordered or unordered.

Did you find this article helpful ? Have you used this technique to build any models ? Do share your experience and suggestions in the comments section below.

About the Author

Sray Agarwal is the chief manager of Bennett Coleman and Co. Ltd. (Times Group) and works as Subject Matter Expert (SME) for Business Analytics program. He has more than 8.5 years of experience in data science and BA.

He holds a degree in Business Analytics from Indian School of Business (ISB), Hyderabad. and graduated with an award of Academic Excellence and has been the part of the Dean’s List. Along with this he is a SAS certified Predictive Modeller.