Treap 学习笔记

Treap 学习笔记

Treap 简介

　　Treap 是一种二叉查找树。它的结构同时满足二叉查找树（Tree）与堆（Heap）的性质，因此得名。Treap的原理是为每一个节点赋一个随机值使其满足堆的性质，保证了树高期望 O(log2n) ，从而保证了时间复杂度。

　　Treap 是一种高效的平衡树算法，在常数大小与代码复杂度上好于 Splay。

Treap 的基本操作

　　现在以 BZOJ 3224 普通平衡树为模板题，详细讨论 Treap 的基本操作。

1.基本结构

　　在一般情况下，Treap 的节点需要存储它的左右儿子，子树大小，节点中相同元素的数量（如果没有可以默认为1），自身信息及随机数的值。

struct node{
int l, r, v, siz, rnd, ct;
}d[1000005];

　　其中

l

为左儿子节点编号，

r

为右儿子节点编号，

v

为节点数值，

siz

为子树大小，

rnd

为节点的随机值，

ct

为该节点数值的出现次数（目的为将所有数值相同的点合为一个）。

2.关于随机值

　　随机值由

rand()

函数生成， 考虑到

<cstdlib>

库中的

rand()

速度较慢，所以在卡常数的时候建议手写

rand()

函数。

inline int rand(){
static int seed = 2333;
return seed = (int)((((seed ^ 998244353) + 19260817ll) * 19890604ll) % 1000000007);
}

　　其中

seed

为随机种子，可以随便填写。

3.节点信息更新

　　节点信息更新由

update()

函数实现。在每次产生节点关系的修改后，需要更新节点信息（最基本的子树大小，以及你要维护的其他内容）。

　　时间复杂度 O(1) 。

inline void update(int k){
d[k].siz = d[lc].siz + d[rc].siz + d[k].ct;
}

4.「重要」左旋与右旋

　　左旋与右旋是 Treap 的核心操作，也是 Treap 动态保持树的深度的关键，其目的为维护 Treap 堆的性质。

　　下面的图片可以让你更好的理解左旋与右旋：

　　


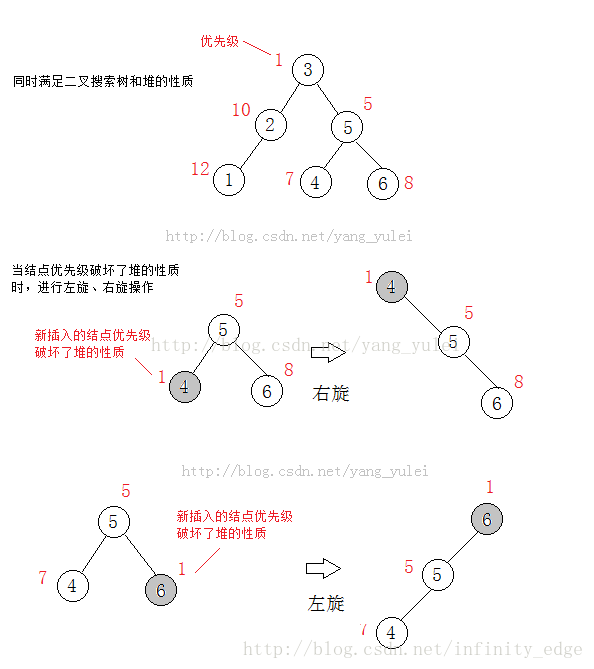
　　下面具体介绍左旋与右旋操作。左旋与右旋均为变更操作节点与其两个儿子的相对位置的操作。

　　「左旋」为将作儿子节点代替根节点的位置， 根节点相应的成为左儿子节点的右儿子（满足二叉搜索树的性质）。相应的，之前左儿子节点的右儿子应转移至之前根节点的左儿子。此时，只有之前的根节点与左儿子节点的

siz

发生了变化。所以要

update()

这两个节点。

　　「右旋」类似于「左旋」，将左右关系相反即可。

　　时间复杂度 O(1) 。

　　请读者思考并彻底理解这个过程。

void rturn(int &k){ //右旋
int t = d[k].l; d[k].l = d[t].r; d[t].r = k;
d[t].siz = d[k].siz; update(k); k = t;
}

void lturn(int &k){ //左旋
int t = d[k].r; d[k].r = d[t].l; d[t].l = k;
d[t].siz = d[k].siz; update(k); k = t;
}

5.节点的插入与删除

　　节点的插入与删除是 Treap 的基本功能之一。

　　「节点的插入」是一个递归的过程，我们从根节点开始，逐个判断当前节点的值与插入值的大小关系。如果插入值小于当前节点值，则递归至左儿子；大于则递归至右儿子；相等则直接在把当前节点数值的出现次数 +1 ，跳出循环即可。如果当前访问到了一个空节点，则初始化新节点，将其加入到 Treap 的当前位置。

　　「节点的删除」同样是一个递归的过程，不过需要讨论多种情况：

　　如果插入值小于当前节点值，则递归至左儿子；大于则递归至右儿子。

　　如果插入值等于当前节点值：

　　　　若当前节点数值的出现次数大于 1 ，则减一;

　　　　若当前节点数值的出现次数等于于 1 :

　　　　　　若当前节点没有左儿子与右儿子，则直接删除该节点（置 0）；

　　　　　　若当前节点没有左儿子或右儿子，则将左儿子或右儿子替代该节点；

　　　　　　若当前节点有左儿子与右儿子，则不断旋转 当前节点，并走到当前节点新的对应位置，直到没有左儿子或右儿子为止。

　　时间复杂度均为 O(log2n) 。

　　具体实现代码如下：

void ins(int &k, int x){
if(k == 0){
k = ++sz;
d[k].siz = d[k].ct = 1; d[k].v = x; d[k].rnd = rand();
return;
}
d[k].siz ++;
if(d[k].v == x) d[k].ct ++;
else if(x > d[k].v){
ins(d[k].r, x);
if(d[rc].rnd < d[k].rnd) lturn(k);
}else{
ins(d[k].l, x);
if(d[lc].rnd < d[k].rnd) rturn(k);
}
}

void del(int &k, int x){
if(k == 0) return;
if(d[k].v == x){
if(d[k].ct > 1){
d[k].ct --; d[k].siz--; return;
}
if(lc == 0 || rc == 0) k = lc + rc;
else if(d[lc].rnd < d[rc].rnd) rturn(k), del(k, x);
else lturn(k), del(k, x);
}else if(x > d[k].v){
d[k].siz --; del(rc, x);
}else{
d[k].siz --; del(lc, x);
}
}

6.查询数x的排名

　　查询数x的排名可以利用在二叉搜索树上的相同方法实现。

　　具体思路为根据递归找到当前节点，并记录小于这个节点的节点的数量（左子树） 。

　　时间复杂度 O(log2n) 。

　　代码实现如下：

int findv(int k, int x){
if(k == 0) return 0;
if(d[k].v == x) return d[lc].siz + 1;
if(x > d[k].v){
return d[lc].siz + d[k].ct + findv(rc, x);
}else{
return findv(lc, x);
}
}

7.查询排名为x的数

　　查询排名为x的数可以利用在二叉搜索树上的相同方法实现。

　　具体思路为根据当前x来判断该数在左子树还是右子树 。

　　时间复杂度 O(log2n) 。

　　代码实现如下：

int findk(int k, int x){
if(k == 0) return 0;
if(x <= d[lc].siz) return findk(lc, x);
x -= d[lc].siz;
if(x <= d[k].ct) return d[k].v;
x -= d[k].ct;
return findk(rc, x);
}

7.查询数的前驱与后继

　　查询数的前驱与后继同样可以递归实现。查前驱即为递归当前数，走到小于等于x的节点，并记录其中最大的。后继同理。

　　时间复杂度 O(log2n) 。

　　代码实现如下：

void pre(int k, int x){ //前驱
if(k == 0) return;
if(d[k].v < x) {
ans = k; return pre(rc, x);
}
else return pre(lc, x);
}

void nxt(int k, int x){ //后继
if(k == 0) return;
if(d[k].v > x) {
ans = k; return nxt(lc, x);
}
else return nxt(rc, x);
}

Treap 模板

BZOJ 3224 普通平衡树

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdio>

#define lc d[k].l
#define rc d[k].r

using namespace std;
typedef long long ll;

inline int rand(){
static int seed = 2333;
return seed = (int)((((seed ^ 998244353) + 19260817ll) * 19890604ll) % 1000000007);
}

struct node{
int l, r, v, siz, rnd, ct;
}d[1000005];

int n, sz, rt, ans;

inline void update(int k){
d[k].siz = d[lc].siz + d[rc].siz + d[k].ct;
}

void rturn(int &k){
int t = d[k].l; d[k].l = d[t].r; d[t].r = k;
d[t].siz = d[k].siz; update(k); k = t;
}

void lturn(int &k){
int t = d[k].r; d[k].r = d[t].l; d[t].l = k;
d[t].siz = d[k].siz; update(k); k = t;
}

void ins(int &k, int x){
if(k == 0){
k = ++sz;
d[k].siz = d[k].ct = 1; d[k].v = x; d[k].rnd = rand();
return;
}
d[k].siz ++;
if(d[k].v == x) d[k].ct ++;
else if(x > d[k].v){
ins(d[k].r, x);
if(d[rc].rnd < d[k].rnd) lturn(k);
}else{
ins(d[k].l, x);
if(d[lc].rnd < d[k].rnd) rturn(k);
}
}

void del(int &k, int x){
if(k == 0) return;
if(d[k].v == x){
if(d[k].ct > 1){
d[k].ct --; d[k].siz--; return;
}
if(lc == 0 || rc == 0) k = lc + rc;
else if(d[lc].rnd < d[rc].rnd) rturn(k), del(k, x);
else lturn(k), del(k, x);
}else if(x > d[k].v){
d[k].siz --; del(rc, x);
}else{
d[k].siz --; del(lc, x);
}
}
int findv(int k, int x){
if(k == 0) return 0;
if(d[k].v == x) return d[lc].siz + 1;
if(x > d[k].v){
return d[lc].siz + d[k].ct + findv(rc, x);
}else{
return findv(lc, x);
}
}

int findk(int k, int x){
if(k == 0) return 0;
if(x <= d[lc].siz) return findk(lc, x);
x -= d[lc].siz;
if(x <= d[k].ct) return d[k].v;
x -= d[k].ct;
return findk(rc, x);
}

void pre(int k, int x){
if(k == 0) return;
if(d[k].v < x) {
ans = k; return pre(rc, x);
}
else return pre(lc, x);
}

void nxt(int k, int x){
if(k == 0) return;
if(d[k].v > x) {
ans = k; return nxt(lc, x);
}
else return nxt(rc, x);
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i ++){
int opt, x;
scanf("%d%d", &opt, &x);
if(opt == 1) ins(rt, x);
if(opt == 2) del(rt, x);
if(opt == 3) printf("%d\n", findv(rt, x));
if(opt == 4) printf("%d\n", findk(rt, x));
if(opt == 5){
ans = 0; pre(rt, x); printf("%d\n", d[ans].v);
}
if(opt == 6){
ans = 0; nxt(rt, x); printf("%d\n", d[ans].v);
}
}
return 0;
}