吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-2)-- 优化算法
2017-11-14 20:06
866 查看
作者: 大树先生
博客: http://blog.csdn.net/koala_tree
知乎:https://www.zhihu.com/people/dashuxiansheng
GitHub:https://github.com/KoalaTree
2017 年 10 月 11 日
以下为在Coursera上吴恩达老师的DeepLearning.ai课程项目中,第二部分《改善深层神经网络:超参数调试、正则化以及优化》第二周课程“优化算法”关键点的笔记。因为这节课每一节的知识点都很重要,所以本次笔记几乎涵盖了全部小视频课程的记录。同时在阅读以下笔记的同时,强烈建议学习吴恩达老师的视频课程,视频请至 Coursera 或者 网易云课堂。
同时我在知乎上开设了关于机器学习深度学习的专栏收录下面的笔记,方便在移动端的学习。欢迎关注我的知乎:大树先生。一起学习一起进步呀!^_^
对整个训练集进行梯度下降法的时候,我们必须处理整个训练数据集,然后才能进行一步梯度下降,即每一步梯度下降法需要对整个训练集进行一次处理,如果训练数据集很大的时候,如有500万或5000万的训练数据,处理速度就会比较慢。
但是如果每次处理训练数据的一部分即进行梯度下降法,则我们的算法速度会执行的更快。而处理的这些一小部分训练子集即称为Mini-batch。

对于普通的梯度下降法,一个epoch只能进行一次梯度下降;而对于Mini-batch梯度下降法,一个epoch可以进行Mini-batch的个数次梯度下降。
普通的batch梯度下降法和Mini-batch梯度下降法代价函数的变化趋势,如下图所示:
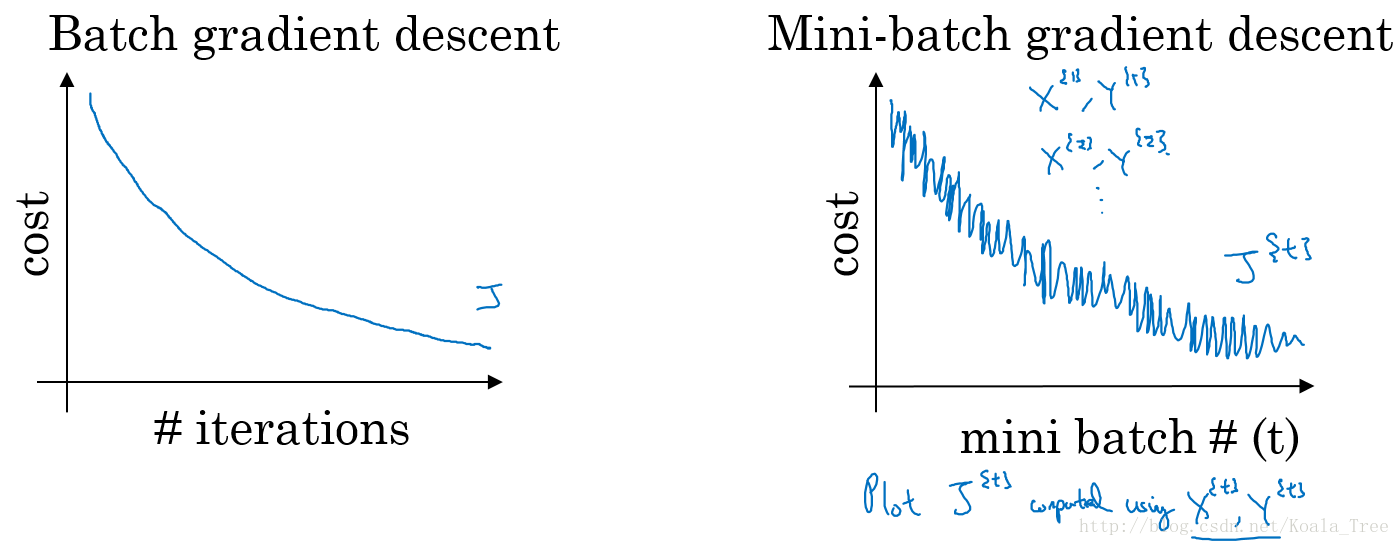
batch梯度下降:
对所有m个训练样本执行一次梯度下降,每一次迭代时间较长;
Cost function 总是向减小的方向下降。
随机梯度下降:
对每一个训练样本执行一次梯度下降,但是丢失了向量化带来的计算加速;
Cost function总体的趋势向最小值的方向下降,但是无法到达全局最小值点,呈现波动的形式。
Mini-batch梯度下降:
选择一个1<size<m 的合适的size进行Mini-batch梯度下降,可以实现快速学习,也应用了向量化带来的好处。
Cost function的下降处于前两者之间。

如果训练样本的大小比较小时,如m⩽2000时
—— 选择batch梯度下降法;
如果训练样本的大小比较大时,典型的大小为:
26、27、⋯、210;
Mini-batch的大小要符合CPU/GPU内存。
指数加权平均的关键函数:
vt=βvt−1+(1−β)θt
下图是一个关于天数和温度的散点图:
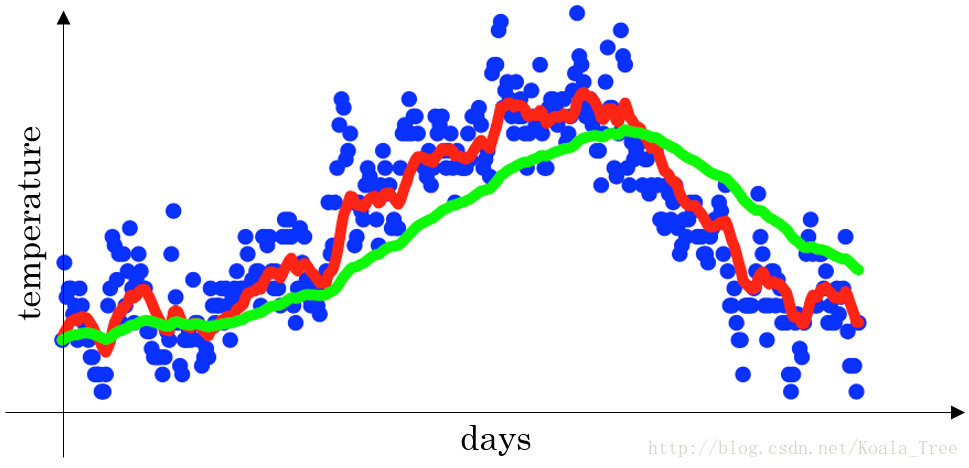
当β=0.9时,指数加权平均最后的结果如图中红色线所示;
当β=0.98时,指数加权平均最后的结果如图中绿色线所示;
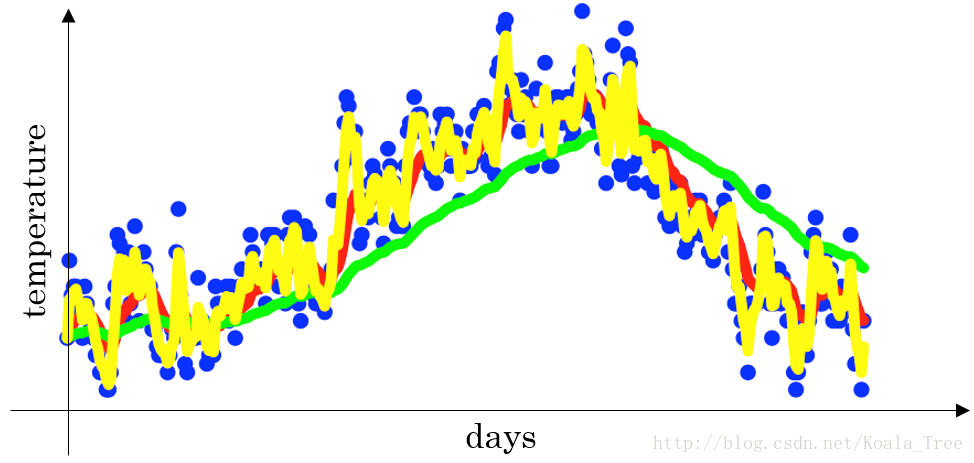
当β=0.5时,指数加权平均最后的结果如下图中黄色线所示;
例子,当β=0.9时:
v100=0.9v99+0.1θ100v99=0.9v98+0.1θ99v98=0.9v97+0.1θ98…
展开:
v100=0.1θ100+0.9(0.1θ99+0.9(0.1θ98+0.9v97))=0.1θ100+0.1×0.9θ99+0.1×(0.9)2θ98+0.1×(0.9)3θ97+⋯
上式中所有θ前面的系数相加起来为1或者接近于1,称之为偏差修正。
总体来说存在,(1−ε)1/ε=1e,在我们的例子中,1−ε=β=0.9,即0.910≈0.35≈1e。相当于大约10天后,系数的峰值(这里是0.1)下降到原来的1e,只关注了过去10天的天气。
v0=0v1=βv0+(1−β)θ1v2=βv1+(1−β)θ2v3=βv2+(1−β)θ3…
因为,在计算当前时刻的平均值,只需要前一天的平均值和当前时刻的值,所以在数据量非常大的情况下,指数加权平均在节约计算成本的方面是一种非常有效的方式,可以很大程度上减少计算机资源存储和内存的占用。
在我们执行指数加权平均的公式时,当β=0.98时,我们得到的并不是图中的绿色曲线,而是下图中的紫色曲线,其起点比较低。
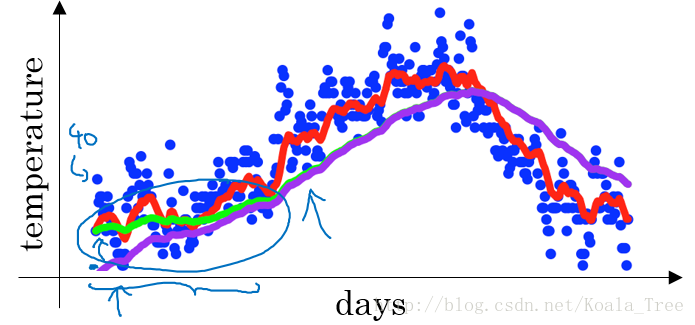
原因:
v0=0v1=0.98v0+0.02θ1=0.02θ1v2=0.98v1+0.02θ2=0.98×0.02θ1+0.02θ2=0.0196θ1+0.02θ2
如果第一天的值为如40,则得到的v1=0.02×40=8,则得到的值要远小于实际值,后面几天的情况也会由于初值引起的影响,均低于实际均值。
偏差修正:
使用vt1−βt
当t=2时:
1−βt=1−(0.98)2=0.0396
v20.0396=0.0196θ1+0.02θ20.0396
偏差修正得到了绿色的曲线,在开始的时候,能够得到比紫色曲线更好的计算平均的效果。随着t逐渐增大,βt接近于0,所以后面绿色的曲线和紫色的曲线逐渐重合了。
虽然存在这种问题,但是在实际过程中,一般会忽略前期均值偏差的影响。
动量梯度下降的基本思想就是计算梯度的指数加权平均数,并利用该梯度来更新权重。
在我们优化 Cost function 的时候,以下图所示的函数图为例:
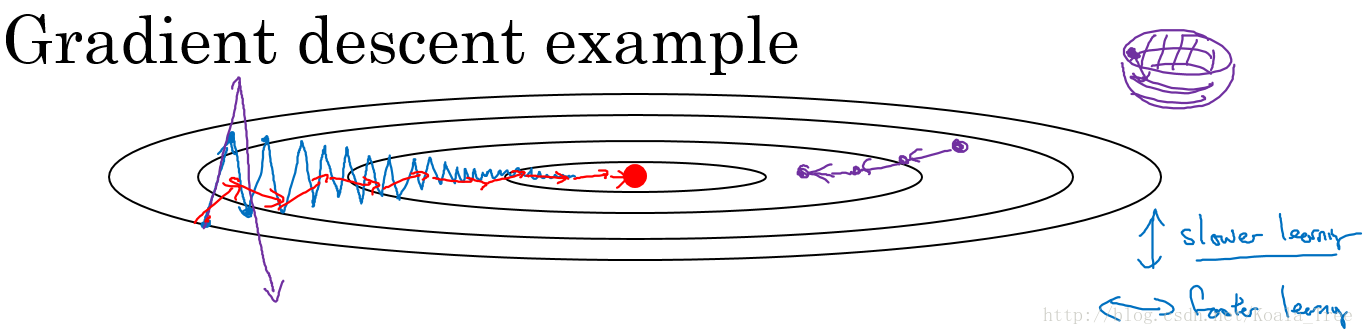
在利用梯度下降法来最小化该函数的时候,每一次迭代所更新的代价函数值如图中蓝色线所示在上下波动,而这种幅度比较大波动,减缓了梯度下降的速度,而且我们只能使用一个较小的学习率来进行迭代。
如果用较大的学习率,结果可能会如紫色线一样偏离函数的范围,所以为了避免这种情况,只能用较小的学习率。
但是我们又希望在如图的纵轴方向梯度下降的缓慢一些,不要有如此大的上下波动,在横轴方向梯度下降的快速一些,使得能够更快的到达最小值点,而这里用动量梯度下降法既可以实现,如红色线所示。
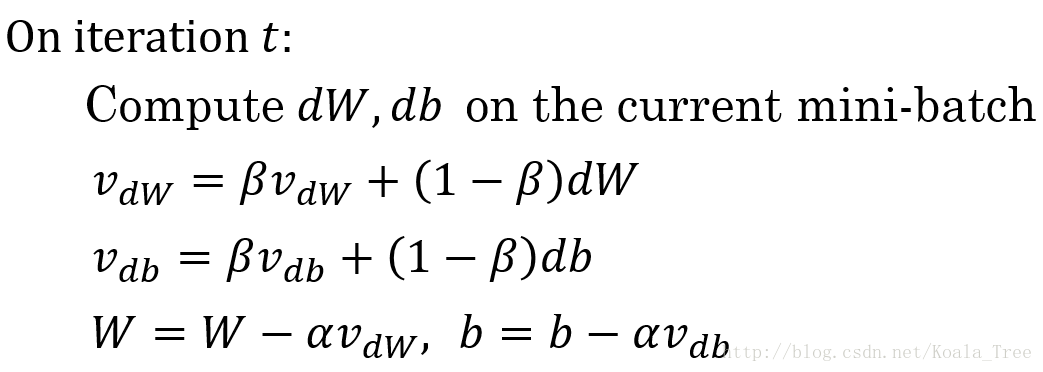
β常用的值是0.9。
在我们进行动量梯度下降算法的时候,由于使用了指数加权平均的方法。原来在纵轴方向上的上下波动,经过平均以后,接近于0,纵轴上的波动变得非常的小;但在横轴方向上,所有的微分都指向横轴方向,因此其平均值仍然很大。最终实现红色线所示的梯度下降曲线。
在对应上面的计算公式中,将Cost function想象为一个碗状,想象从顶部往下滚球,其中:
微分项dw,db想象为球提供的加速度;
动量项vdw,vdb相当于速度;
小球在向下滚动的过程中,因为加速度的存在速度会变快,但是由于β的存在,其值小于1,可以认为是摩擦力,所以球不会无限加速下去。
除了上面所说的Momentum梯度下降法,RMSprop(root mean square prop)也是一种可以加快梯度下降的算法。
同样算法的样例实现如下图所示:
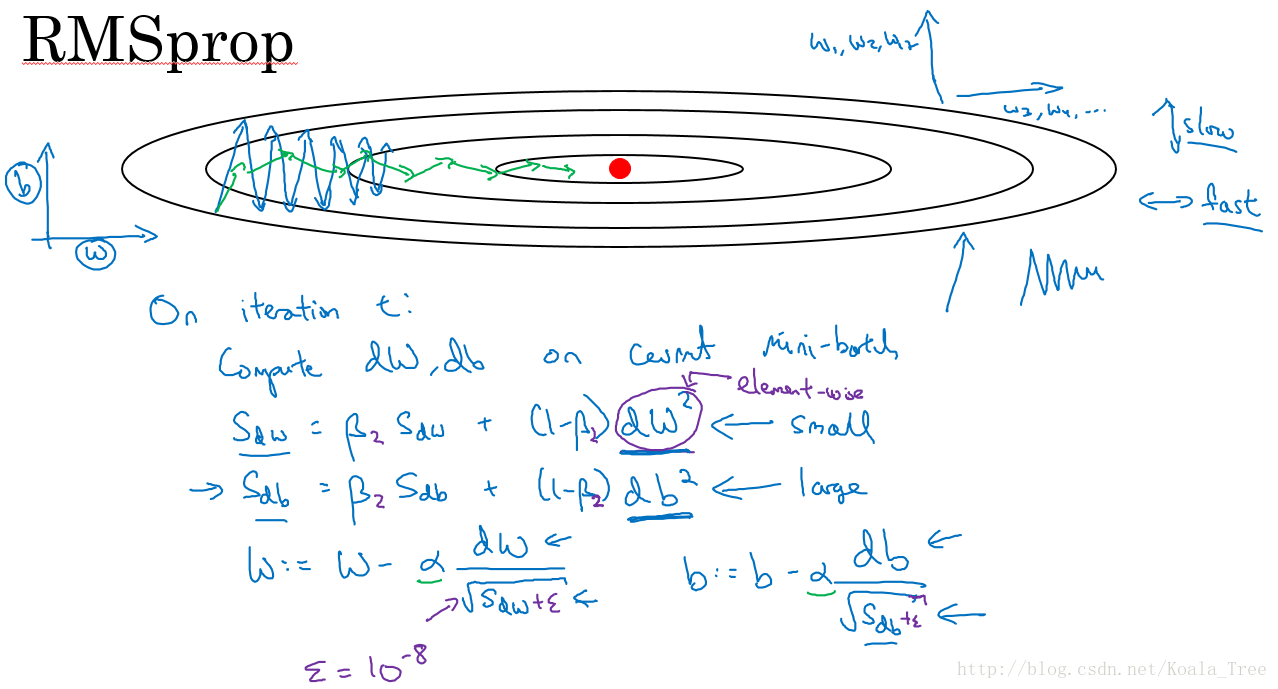
这里假设参数b的梯度处于纵轴方向,参数w的梯度处于横轴方向(当然实际中是处于高维度的情况),利用RMSprop算法,可以减小某些维度梯度更新波动较大的情况,如图中蓝色线所示,使其梯度下降的速度变得更快,如图绿色线所示。
在如图所示的实现中,RMSprop将微分项进行平方,然后使用平方根进行梯度更新,同时为了确保算法不会除以0,平方根分母中在实际使用会加入一个很小的值如ε=10−8。
Adam 优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法。
初始化:Vdw=0,Sdw=0,Vdb=0,Sdb=0
第t次迭代:
Compute dw,db on
the current mini-batch
Vdw=β1Vdw+(1−β1)dw,Vdb=β1Vdb+(1−β1)db <–“Momentum”
Sdw=β2Sdw+(1−β2)(dw)2,Sdb=β2Sdb+(1−β2)(db)2 <–“RMSprop”
Vcorrecteddw=Vdw/(1−βt1),Vcorrecteddb=Vdb/(1−βt1) <–
偏差修正
Scorrecteddw=Sdw/(1−βt2),Scorrecteddb=Sdb/(1−βt2) <–
偏差修正
w:=w−αVcorrecteddwScorrecteddw−−−−−−−√+ε,b:=b−αVcorrecteddbScorrecteddb−−−−−−−√+ε
α:需要进行调试;
β1:常用缺省值为0.9,dw的加权平均;
β2:推荐使用0.999,dw2的加权平均值;
ε:推荐使用10−8。
Adam代表的是Adaptive Moment Estimation。
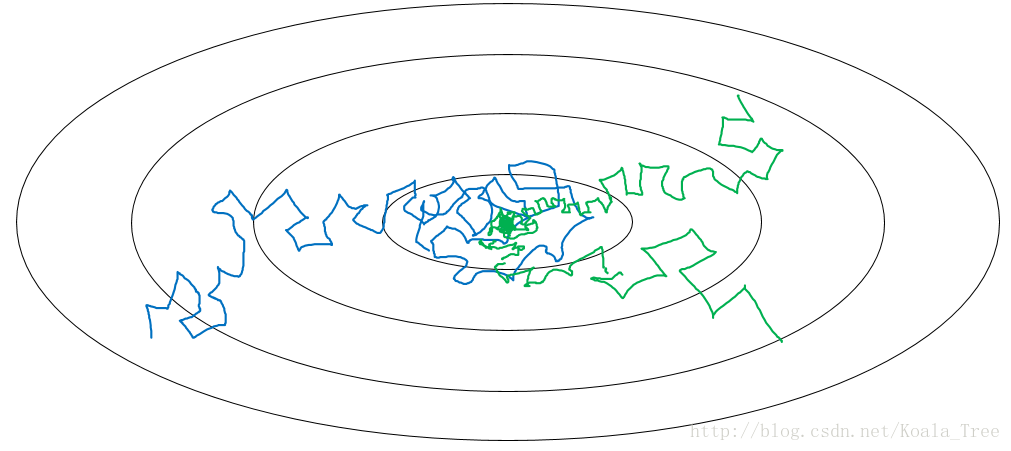
在我们利用 mini-batch 梯度下降法来寻找Cost function的最小值的时候,如果我们设置一个固定的学习速率α,则算法在到达最小值点附近后,由于不同batch中存在一定的噪声,使得不会精确收敛,而一直会在一个最小值点较大的范围内波动,如下图中蓝色线所示。
但是如果我们使用学习率衰减,逐渐减小学习速率α,在算法开始的时候,学习速率还是相对较快,能够相对快速的向最小值点的方向下降。但随着α的减小,下降的步伐也会逐渐变小,最终会在最小值附近的一块更小的区域里波动,如图中绿色线所示。
常用:
α=11+decay_rate∗epoch_numα0
指数衰减:
α=0.95epoch_numα0
其他:
α=kepoch_num⋅α0
离散下降(不同阶段使用不同的学习速率)
在低纬度的情形下,我们可能会想象到一个Cost function 如左图所示,存在一些局部最小值点,在初始化参数的时候,如果初始值选取的不得当,会存在陷入局部最优点的可能性。
但是,如果我们建立一个神经网络,通常梯度为零的点,并不是如左图中的局部最优点,而是右图中的鞍点(叫鞍点是因为其形状像马鞍的形状)。
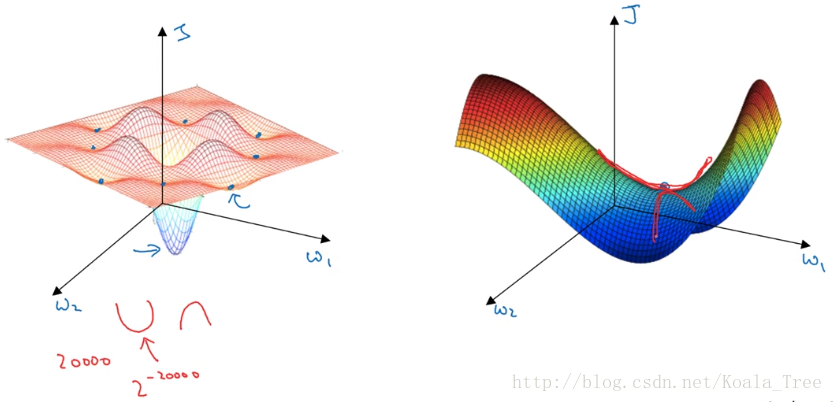
在一个具有高维度空间的函数中,如果梯度为0,那么在每个方向,Cost function可能是凸函数,也有可能是凹函数。但如果参数维度为2万维,想要得到局部最优解,那么所有维度均需要是凹函数,其概率为2−20000,可能性非常的小。也就是说,在低纬度中的局部最优点的情况,并不适用于高纬度,我们在梯度为0的点更有可能是鞍点。
在高纬度的情况下:
* 几乎不可能陷入局部最小值点;
* 处于鞍点的停滞区会减缓学习过程,利用如Adam等算法进行改善。
博客: http://blog.csdn.net/koala_tree
知乎:https://www.zhihu.com/people/dashuxiansheng
GitHub:https://github.com/KoalaTree
2017 年 10 月 11 日
以下为在Coursera上吴恩达老师的DeepLearning.ai课程项目中,第二部分《改善深层神经网络:超参数调试、正则化以及优化》第二周课程“优化算法”关键点的笔记。因为这节课每一节的知识点都很重要,所以本次笔记几乎涵盖了全部小视频课程的记录。同时在阅读以下笔记的同时,强烈建议学习吴恩达老师的视频课程,视频请至 Coursera 或者 网易云课堂。
同时我在知乎上开设了关于机器学习深度学习的专栏收录下面的笔记,方便在移动端的学习。欢迎关注我的知乎:大树先生。一起学习一起进步呀!^_^
改善深层神经网络:超参数调试、正则化以及优化 —优化算法
1. Mini-batch 梯度下降法
对整个训练集进行梯度下降法的时候,我们必须处理整个训练数据集,然后才能进行一步梯度下降,即每一步梯度下降法需要对整个训练集进行一次处理,如果训练数据集很大的时候,如有500万或5000万的训练数据,处理速度就会比较慢。但是如果每次处理训练数据的一部分即进行梯度下降法,则我们的算法速度会执行的更快。而处理的这些一小部分训练子集即称为Mini-batch。
算法核心:

对于普通的梯度下降法,一个epoch只能进行一次梯度下降;而对于Mini-batch梯度下降法,一个epoch可以进行Mini-batch的个数次梯度下降。
不同size大小的比较
普通的batch梯度下降法和Mini-batch梯度下降法代价函数的变化趋势,如下图所示:
batch梯度下降:
对所有m个训练样本执行一次梯度下降,每一次迭代时间较长;
Cost function 总是向减小的方向下降。
随机梯度下降:
对每一个训练样本执行一次梯度下降,但是丢失了向量化带来的计算加速;
Cost function总体的趋势向最小值的方向下降,但是无法到达全局最小值点,呈现波动的形式。
Mini-batch梯度下降:
选择一个1<size<m 的合适的size进行Mini-batch梯度下降,可以实现快速学习,也应用了向量化带来的好处。
Cost function的下降处于前两者之间。

Mini-batch 大小的选择
如果训练样本的大小比较小时,如m⩽2000时—— 选择batch梯度下降法;
如果训练样本的大小比较大时,典型的大小为:
26、27、⋯、210;
Mini-batch的大小要符合CPU/GPU内存。
2. 指数加权平均
指数加权平均的关键函数:vt=βvt−1+(1−β)θt
下图是一个关于天数和温度的散点图:

当β=0.9时,指数加权平均最后的结果如图中红色线所示;
当β=0.98时,指数加权平均最后的结果如图中绿色线所示;
当β=0.5时,指数加权平均最后的结果如下图中黄色线所示;

理解指数加权平均
例子,当β=0.9时:v100=0.9v99+0.1θ100v99=0.9v98+0.1θ99v98=0.9v97+0.1θ98…
展开:
v100=0.1θ100+0.9(0.1θ99+0.9(0.1θ98+0.9v97))=0.1θ100+0.1×0.9θ99+0.1×(0.9)2θ98+0.1×(0.9)3θ97+⋯
上式中所有θ前面的系数相加起来为1或者接近于1,称之为偏差修正。
总体来说存在,(1−ε)1/ε=1e,在我们的例子中,1−ε=β=0.9,即0.910≈0.35≈1e。相当于大约10天后,系数的峰值(这里是0.1)下降到原来的1e,只关注了过去10天的天气。
指数加权平均实现
v0=0v1=βv0+(1−β)θ1v2=βv1+(1−β)θ2v3=βv2+(1−β)θ3…因为,在计算当前时刻的平均值,只需要前一天的平均值和当前时刻的值,所以在数据量非常大的情况下,指数加权平均在节约计算成本的方面是一种非常有效的方式,可以很大程度上减少计算机资源存储和内存的占用。
指数加权平均的偏差修正
在我们执行指数加权平均的公式时,当β=0.98时,我们得到的并不是图中的绿色曲线,而是下图中的紫色曲线,其起点比较低。
原因:
v0=0v1=0.98v0+0.02θ1=0.02θ1v2=0.98v1+0.02θ2=0.98×0.02θ1+0.02θ2=0.0196θ1+0.02θ2
如果第一天的值为如40,则得到的v1=0.02×40=8,则得到的值要远小于实际值,后面几天的情况也会由于初值引起的影响,均低于实际均值。
偏差修正:
使用vt1−βt
当t=2时:
1−βt=1−(0.98)2=0.0396
v20.0396=0.0196θ1+0.02θ20.0396
偏差修正得到了绿色的曲线,在开始的时候,能够得到比紫色曲线更好的计算平均的效果。随着t逐渐增大,βt接近于0,所以后面绿色的曲线和紫色的曲线逐渐重合了。
虽然存在这种问题,但是在实际过程中,一般会忽略前期均值偏差的影响。
3. 动量(Momentum)梯度下降法
动量梯度下降的基本思想就是计算梯度的指数加权平均数,并利用该梯度来更新权重。在我们优化 Cost function 的时候,以下图所示的函数图为例:

在利用梯度下降法来最小化该函数的时候,每一次迭代所更新的代价函数值如图中蓝色线所示在上下波动,而这种幅度比较大波动,减缓了梯度下降的速度,而且我们只能使用一个较小的学习率来进行迭代。
如果用较大的学习率,结果可能会如紫色线一样偏离函数的范围,所以为了避免这种情况,只能用较小的学习率。
但是我们又希望在如图的纵轴方向梯度下降的缓慢一些,不要有如此大的上下波动,在横轴方向梯度下降的快速一些,使得能够更快的到达最小值点,而这里用动量梯度下降法既可以实现,如红色线所示。
算法实现
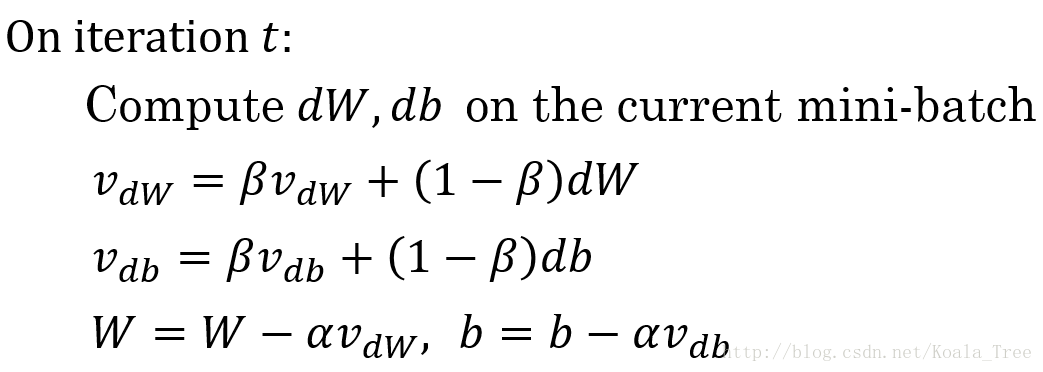
β常用的值是0.9。
在我们进行动量梯度下降算法的时候,由于使用了指数加权平均的方法。原来在纵轴方向上的上下波动,经过平均以后,接近于0,纵轴上的波动变得非常的小;但在横轴方向上,所有的微分都指向横轴方向,因此其平均值仍然很大。最终实现红色线所示的梯度下降曲线。
算法本质解释
在对应上面的计算公式中,将Cost function想象为一个碗状,想象从顶部往下滚球,其中:微分项dw,db想象为球提供的加速度;
动量项vdw,vdb相当于速度;
小球在向下滚动的过程中,因为加速度的存在速度会变快,但是由于β的存在,其值小于1,可以认为是摩擦力,所以球不会无限加速下去。
4. RMSprop
除了上面所说的Momentum梯度下降法,RMSprop(root mean square prop)也是一种可以加快梯度下降的算法。同样算法的样例实现如下图所示:

这里假设参数b的梯度处于纵轴方向,参数w的梯度处于横轴方向(当然实际中是处于高维度的情况),利用RMSprop算法,可以减小某些维度梯度更新波动较大的情况,如图中蓝色线所示,使其梯度下降的速度变得更快,如图绿色线所示。
在如图所示的实现中,RMSprop将微分项进行平方,然后使用平方根进行梯度更新,同时为了确保算法不会除以0,平方根分母中在实际使用会加入一个很小的值如ε=10−8。
5. Adam 优化算法
Adam 优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法。
算法实现
初始化:Vdw=0,Sdw=0,Vdb=0,Sdb=0第t次迭代:
Compute dw,db on
the current mini-batch
Vdw=β1Vdw+(1−β1)dw,Vdb=β1Vdb+(1−β1)db <–“Momentum”
Sdw=β2Sdw+(1−β2)(dw)2,Sdb=β2Sdb+(1−β2)(db)2 <–“RMSprop”
Vcorrecteddw=Vdw/(1−βt1),Vcorrecteddb=Vdb/(1−βt1) <–
偏差修正
Scorrecteddw=Sdw/(1−βt2),Scorrecteddb=Sdb/(1−βt2) <–
偏差修正
w:=w−αVcorrecteddwScorrecteddw−−−−−−−√+ε,b:=b−αVcorrecteddbScorrecteddb−−−−−−−√+ε
超参数的选择
α:需要进行调试;β1:常用缺省值为0.9,dw的加权平均;
β2:推荐使用0.999,dw2的加权平均值;
ε:推荐使用10−8。
Adam代表的是Adaptive Moment Estimation。
6. 学习率衰减
在我们利用 mini-batch 梯度下降法来寻找Cost function的最小值的时候,如果我们设置一个固定的学习速率α,则算法在到达最小值点附近后,由于不同batch中存在一定的噪声,使得不会精确收敛,而一直会在一个最小值点较大的范围内波动,如下图中蓝色线所示。但是如果我们使用学习率衰减,逐渐减小学习速率α,在算法开始的时候,学习速率还是相对较快,能够相对快速的向最小值点的方向下降。但随着α的减小,下降的步伐也会逐渐变小,最终会在最小值附近的一块更小的区域里波动,如图中绿色线所示。

学习率衰减的实现
常用:α=11+decay_rate∗epoch_numα0
指数衰减:
α=0.95epoch_numα0
其他:
α=kepoch_num⋅α0
离散下降(不同阶段使用不同的学习速率)
6. 局部最优问题
在低纬度的情形下,我们可能会想象到一个Cost function 如左图所示,存在一些局部最小值点,在初始化参数的时候,如果初始值选取的不得当,会存在陷入局部最优点的可能性。但是,如果我们建立一个神经网络,通常梯度为零的点,并不是如左图中的局部最优点,而是右图中的鞍点(叫鞍点是因为其形状像马鞍的形状)。

在一个具有高维度空间的函数中,如果梯度为0,那么在每个方向,Cost function可能是凸函数,也有可能是凹函数。但如果参数维度为2万维,想要得到局部最优解,那么所有维度均需要是凹函数,其概率为2−20000,可能性非常的小。也就是说,在低纬度中的局部最优点的情况,并不适用于高纬度,我们在梯度为0的点更有可能是鞍点。
在高纬度的情况下:
* 几乎不可能陷入局部最小值点;
* 处于鞍点的停滞区会减缓学习过程,利用如Adam等算法进行改善。
相关文章推荐
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-2)-- 优化算法
- 1.3 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-4)-- 为什么深度学习会兴起?
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(3-2)-- 机器学习策略(2)(转)
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(3-1)-- 机器学习策略(1)
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-2)-- 神经网络基础(转载)
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-4)-- 特殊应用:人脸识别和神经风格迁移
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-3)-- 目标检测
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-3)-- 超参数调试 和 Batch Norm
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-1)-- 卷积神经网络基础
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-3)-- 浅层神经网络(转载)
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-4)-- 特殊应用:人脸识别和神经风格迁移
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-1)-- 深度学习的实践方面
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-2)-- 深度卷积模型
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-4)-- 深层神经网络(转载)
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-3)-- 目标检测
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(5-1)-- 循环神经网络
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-4)-- 深层神经网络
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-2)-- 神经网络基础
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-3)-- 超参数调试 和 Batch Norm
- 吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-2)-- 神经网络基础
