台湾大学机器学习基石Lecture12

12-1:Quadratic Hypothesis

二次规划的假设

之前我们介绍的都是线性假设，即用一条线将数据分隔开，例如下面的情形：



直观的第一感受就是可以用一条直线将O和X分隔开，由此也引入了得分函数s=wTx。但是如果数据集的分布是下面这个样子呢？



如果你想用一条直线将圈圈和叉叉分开，除非是数据是存在noise的，不然不可能分得开，换个角度想，分开两类数据未必需要直线，例如：



这个黑色的圆圈正好perfect的分开了两类数据，但是这就不是线性的边界啦。由此我们也得到了这个边界是Circular Separable（圆形可分），例如上面的例子，它就可以用一个半径为0.6−−−√的圆来区分两种数据，它的hypothesis就可以用下面的式子定量表示了：

hSEP(x)=sign(−x21−x22+0.6)

但是我们不熟悉这种非线性假设，能不能将其转换为线性假设呢？我们对上面的式子做下面的转换：



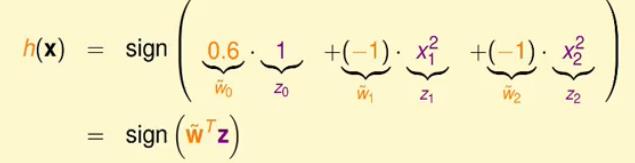
首先令z1=x21,z2=x22,当然为了和PLA一样，补充z0=1，同样的，令w˘0=0.6,w˘1=−1,w˘2=−1(这里的w˘是为了区分之前线性假设中的权重w)，那么我们就得到了（z0,z1,z2）以及权重(w˘0,w˘1,w˘2)，原来的假设h就变成了：

h(x)=sign(wT˘z)

这就是我们很熟悉的线性假设了，这里就是把原来是圆形可分的资料(xn,yn)变成了线性可分的资料(zn,yn)，相当于作了一个非线性特征变换ϕ，直观的对比如下所示：



从图中可以看出，就是把圆内的数据点变换为线性可分中直线下面的数据点，黑色的圆圈变为右边黑色的直线。

上面是已知在x域中是圆形可分的，对应到z域中就是线性可分的，那么反过来，在z域中线性可分，转换为x域中一定是圆形可分吗？答案不是的，因为转换回x域可以有很多种情形，

考虑下面的情形：

z=（z0,z1,z2）=ϕ(x)=(1,x21,x22)

h(x)=sign(wT˘z)=sign(w˘0+w˘1x21+w˘2x22)，其中w˘=(w˘0,w˘1,w˘2)

我们分别取不同的w˘，看转为x域是否有不同？

1. 取(w˘0,w˘1,w˘2)=(0.6,−1,−1)，这个就是上面介绍的例子了，x域中是圆形可分的。

2. 取(w˘0,w˘1,w˘2)=(−0.6,+1,+1)，当然这也是圆形可分的，和上面不同的是，在圆外的数据点是O,圆内的数据点是X。

3. 取(w˘0,w˘1,w˘2)=(0.6,−1,−2)，即(0.6−x21−2x22)，令这个式子为0，在x域中，你会很容易发现这是一个椭圆而非圆形可分，这也就验证了上面的结论。

4. 再举最后一个特例， 取(w˘0,w˘1,w˘2)=(0.6,+1,+1)，即(0.6+x21+x22)，平方项+0.6，无论怎么样都会是正的啊，对应回x域也就是所有O了。

综上，我们应该可以得到下面的结论：

Z空间的直线 <=> X空间的二次曲线

上面的例子是圆心在原点的情况，这是一个特例。我们考虑一般情形，一般情形的非线性转换应该是下面这个样子的：

ϕ2(x)={1,x1,x2,x21,x1x2,x22}(个人理解就是比如原来是2个输入特征（x1,x2）,但是现在转换出来了6项，也就是增加更多的特征，而这个增加的特征是通过已知的特征之间组合而来的，所以就能够在Z空间线性可分。)

从上面我们就可以推出一般的Z空间中的hypothesis为：



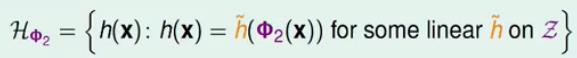
说了这么多，我们举一个具体的实例：

例如在X空间中有椭圆2(x1+x2−3)2+(x1−x2−4)2=1，由这个式子，怎么推出Z空间中的权重w˘？

将上式化解开，合并相同的项后得到下面的式子：

33−20x1−4x2+3x21+2x1x2+3x22=0

对比ϕ2(x)={1,x1,x2,x21,x1x2,x22}，我们就能得到权重w˘=[33,−20,−4,3,2,3].

12-2:Nonlinear Transform

非线性变换

从上一节中看出，我们的目标就是在Z空间中找到一条最佳的分类线。并且X空间和Z空间存在下面的诸多联系：



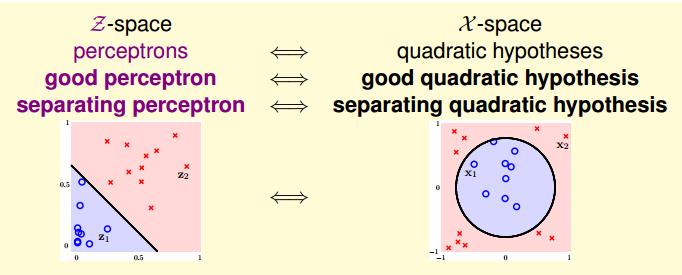
具体的就不细说了，那么如何才能得到这条最佳的分类线呢?

首先把原始的数据(xn,yn)通过非线性变换ϕ(x)变为Z空间的数据(zn=ϕ(xn),yn)

可以使用你想要的任何分类算法（比如PLA），使用数据点(zn,yn)来得Z空间的权重w˘

我们将得到的w˘返回，就能得到最终的假设g(x)=sign(w˘Tϕ(x))

即非线性模型=非线性转换+线性模型，具体流图如下：

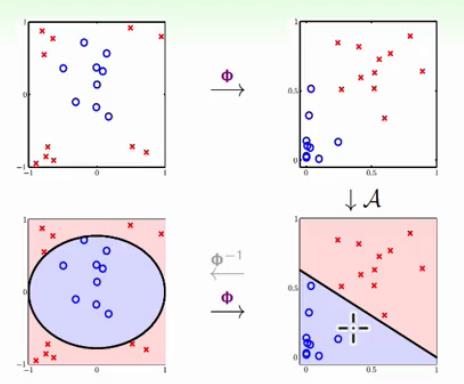
12-3:Price of Nonlinear Transform

非线性变换的代价

非线性变换确实可以转换为线性来做，但是要付出很大的代价，其一就是计算复杂度的提高，比如输入(x1,x2)，转为一般的Z空间来计算的话就是ϕ2(x)={1,x1,x2,x21,x1x2,x22}，更一般的式子就是：

对于特征是二维的来说，原X空间有d个特征，那么对应的Z空间（我们也称之为特征）的数量为1+c1d+c2d+d=d(d+3)2+1（即常数项+单个项+不同的x相乘的项+平方项）。



如果像上面的那副图那样子呢？也就是阶数更高呢？假设阶数为Q，且原X空间为维度为d，那么对应的Z空间特征维度是CQQ+d=CdQ+d,也就是其复杂度为O(Qd)，可以看出来，随着Q和d的变大，其计算复杂度以及空间复杂度是很可怕的。

另一方面，我们考虑一下自由度的问题，Lecture7中，我们知道对于d个输入，其dvc=d+1，那么推广到Z空间，其dvc应该有类似的结论，即dvc=d˘+1，这里的d˘是区分d的表示形式，上面我们知道了复杂度为O(Qd)，也就表明权重w˘的自由度也会增大，即模型复杂度就会提高，那么由此得到的模型泛化能力就会很差。

即阶数Q大=>dvc大

下面我们从视觉角度说明一下这个问题：



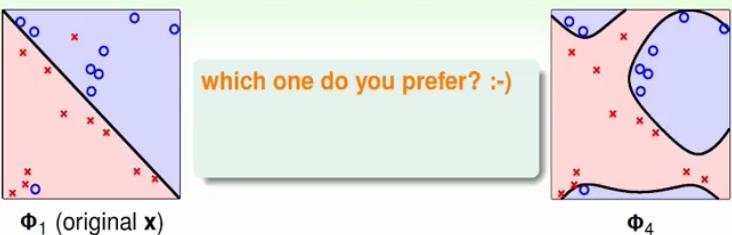
上面图中两种分类假设你会选择哪一个？毫无疑问，坑定左边的，虽然左边有误差，但是模型复杂度很低，模型的泛化能力更好，右边的图虽然Ein(g)=0，但是其Eout(g)肯定是很大的，因为E(out)≤Ein+模型复杂度，那么模型复杂的话，泛化能力就没法保证了。

我们由此又想起了两个老朋友：

1. 我们能否保证Eout和Ein是足够接近的？

2. 我们能否保证Ein足够小？

对比不同的结果，我们可以得到类似的结论如下表：

d˘(Q)	1	2
大	不能保证，模型复杂度高	能保证，选择更多
小	能保证，因为模型复杂度低，由霍夫丁不等式可以得出	不能保证，选择太少了

现在有到了关键的问题，那么如何选择Q呢？

我们可以像上面一样继续用眼睛来选择Q吗？如果这样子你会犯了很大的错误。

例如：一般X空间中2个特征的转换到Z空间为ϕ2(x)={1,x1,x2,x21,x1x2,x22}，我们能不能减少它的复杂度，比如只用ϕ2(x)={1,x21,x22}，这时候dvc=3了,减少了吧？貌似还可以继续减少，比如用ϕ2(x)={1，x21+x22},现在dvc=2了，或者更甚，ϕ2(x)=sign(0.6−x21−x22)，哇，现在dvc=1了，事实上这还是ML吗？你加入了人脑的作用，人脑的复杂度可比公式什么的高太多，实际上这个模型的复杂度特别高。

综上，为了VC安全，一般是保留原来的多项式特征，避免人为的影响。

12-4:Structured Hypothesis Sets

结构化的假设集合

我们考虑从X空间转换到Z空间的多项式变换，那么当变换为0次的时候，那么对应的多项式变换函数：

ϕ0(x)=1

当变换为1次的时候，对应的多项式变换函数：

ϕ1(x)=(ϕ0(x),x1,x2,…xd)

当变换为2次的时候，对应的多项式变换函数：

ϕ2(x)=(ϕ1(x),x21,x1x2,…x2d)

当变换为Q次的时候，对应的多项式变换函数：

ϕQ(x)=(ϕQ−1(x),xQ1,xQ−11x2,…xQd)

将上面的ϕQ(x)定义为HϕQ,那么我们可以得到下面的关系式：

Hϕ0⊂Hϕ1⊂⋯⊂HϕQ

更简单的将Hϕ0记为H0，那么即

H0⊂H1⊂⋯⊂HQ

我们把这种结构称为Structured Hypothesis Sets,即如下图所示：



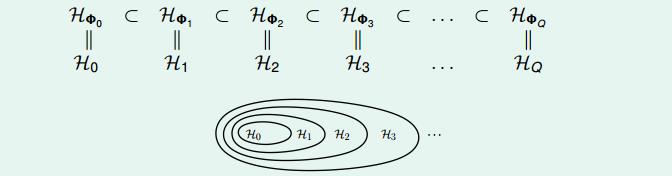
对于这种结构，其对应的VC维数呢？应该有：

dVC(H0)≤dVC(H1)≤⋯

当然对应的错误Ein就应该和VC维相反了，即：

Ein(H0)≥Ein(H1)≥⋯

我们考虑下面的情形：



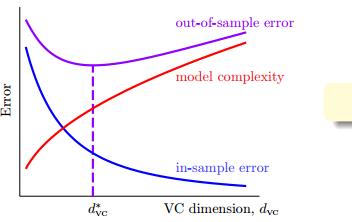
举个例子，我们是否一定可以得出多项式变换Q阶数越高越好？其实从上图可以看出，Eout最小点的时候存在且为d∗vc，并且它是处于模型复杂度差不多的位置，所以比如像H1126的模型其效果并不会很好，因为模型复杂度太高了，所以并不是Ein越小，模型越优秀。

现实中如何选择一个比较好的模型呢？

实际上我们可以使用H1，即从低阶开始，然后判断Ein是否足够好了，不是很好就尝试H2，依次类推。。。

这样子虽然浪费了计算，但是它是一种足够安全的做法，能够有效的防止过拟合。