台湾大学机器学习基石Lecture9

9-1：Linear Regress Problem

线性回归问题

再次谈到第二章发银行信用卡的问题，给你X=(x1,x2…xn)个输入特征，二元分类就是让你设计一个算法决定是否给一个新的顾客发放信用卡，而本节介绍的回归问题是指对于一个新的顾客，你设计一个算法来预测该顾客的信用额度是多少，它的输入是整个实数集R。

线性回归的假设公式如下：

y≈∑di=0wi⋅xi，将公式用向量表示为：h(x)=WT⋅X，这个公式类似于PLA，PLA的公式为h(x)=sign(WT⋅X)，回归问题只是没有sign符号。

线性回归问题图形化描述：



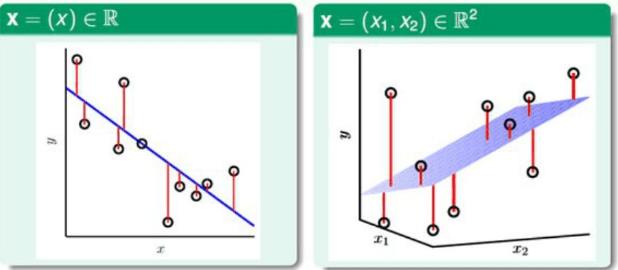
左边的图片是在一维中找寻一条直线，右边的图片是在二维中找到一个平面，依次类推…线性回归问题就是找到一条线/一个平面/一个超平面来拟合数据，使这条线/这个平面/这个超平面与已知的数据点之间的总剩余误差（residual）最小，从而进行预测。其中residual（剩余误差）就如图中所示的红线，代表各个点和分离的线或面的距离（即方程计算得到yˇ和标签y之间的绝对值大小）。

那么我们首先要对这个误差进行衡量，常用的误差衡量方式也就是Squared error（平方误差），这里要区分一下最小二乘。如下式所示：

err(yˇ,y)=(yˇ−y)2

那么对应的利用Squared error得到Ein(h)和Eout(h)的计算公式如下：

Ein(h)=1N∑Nn=1(h(xn)−yn))2

=1N∑Nn=1(wT⋅xn−yn)2

Eout(h)=E(x,y) p(WT⋅x−y)2

因为h和w总是一 一对应的关系，那么将从现在开始用w替换h，也就是上面的Ein(h)和Eout(h)会变成Ein(w)和Eout(w)。

VC限制对回归问题同样适用，那么接下来的问题就是如何最小化Ein(w)?对应的Eout(w)同样也会最小。

9-2：Linear Regress Algorithm

线性回归算法

针对上一节得到的Ein(w)我们对它进行下面的变换操作。

Ein(w)=1N∑Nn=1(wT⋅xn−yn)2

=1N∑Nn=1(xTn⋅w−yn)2



其中x是N×(d+1)维，w是(d+1)×1维的，y是N×1维的。

现在我们的目标就变成了：

minEin(w)=1N||(x⋅W−y)||2

这个函数的长相类似于二次函数，如下图所示：



从图中可以看出，它是光滑的、可微分的、连续的，最重要对的一点是它是凸函数(convex)（这里好像和大学我自己学的凸函数的定义完全反了，大学是上凸下凹，这边是上凹下凸，就好好记住吧！），对于凸函数，那么它的最小化所得到的w就是图中最低点（黑点），如何求这个最低点呢？

如何计算w，我们可以利用偏导数为0来计算w，为什么呢？例如一个小球放在山上，偏导数不为0相当于小球不是在最低点的时候，那么小球肯定还可以向其他方向滚，什么时候小球不滚了呢，那就是到达最低点，也就是山谷，所以我们的目标就是寻找偏导数为0的点。

偏导数的定义矩阵如下所示：



下面对Ein(w)作进一步变换：

Ein(w)=1N||(x⋅W−y)||2

=1N(wTxTxw−2wTxTy+yTy)

这个式子求偏导数可能一下子看不出来，我们考虑一个简单的式子：

假设Ein(w)=1N(aw2−2bw+c)（其中a,b,c是常数）

那么它的偏导数∇Ein(w)=1N(2aw−2b)

用这个套路，算上面的偏导数，令a=xTx,b=xTy,c=yTy，那么得到最终的偏导数表达式为：

∇Ein(w)=2N(xTxw−xTy)

令Ein(w)=0我们可以求出w，可是要分两种情况讨论:

(xTx)可逆：令Ein(w)=0，即(xTxw−xTy)=0，稍微变换一下得到

w=(xTx)−1xTy，并且令x+=(xTx)−1xT称为矩阵x的伪逆。

(xTx)不可逆：那么存在不止一组解，用其他的方式求出伪逆x+，选择其中一个进行w=x+y求解y就可以了。

总结下线性回归的求解步骤：

1. 通过数据集D构建输入矩阵X和输出矩阵y，它们对应的维度分别如下图所示。



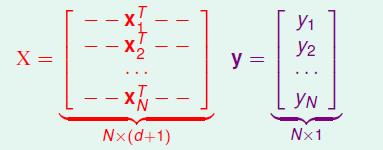
2. 利用x+=(xTx)−1xT计算伪逆x+

3. 返回wLIN=x+y

9-3：Generalization issue

泛化问题

现在有一个问题就是上一节求解出来的最优解过程有没有在学习，也就是是不是机器学习算法，因为上一节用的是解析解的形式，不像PLA，一步一步迭代求出的minEin(w)。

对于泛化问题，即(Eout−Ein)≈0，其实由于VC维的限制，我们能够保证这是一个机器学习算法，因为我们使得Ein(w)很小，其结果Eout(w)也会很小，那么这就达到了机器学习的目的。

首次给出Ein平均的式子结果表示，其用Ein¯表示：

Ein¯=ED−pN[Ein(WLIN)w.r.t D]=noise level⋅(1−d+1N)（3）

其中noise level表示数据D中存在的噪声数据，(d+1)是参数个数，N是样本总数。

接下来证明为什么求出的Ein¯能表示成上面的式子(3)？

上一节中我们得到了如下式子：

minEin(w)=1N||(x⋅W−y)||2，我们将这个式子中的W用WLIN替换掉，因为WLIN能求出好的Ein，只有好的Ein才能求出好的Eout，变换后的式子为：

Ein(WLIN)=1N||y^−y)||2(其中y^=WTx)

=1N||y−xx+y||2

=1N||(I−xx+)y||2

我们把(I−xx+)称为帽子矩阵(hat matrix)H，所以我们得到了：

Ein¯=1N||(I−H)y)||2

光从式子我们很难得到结论，我们考虑以下矩阵H的物理意义，如下图所示：



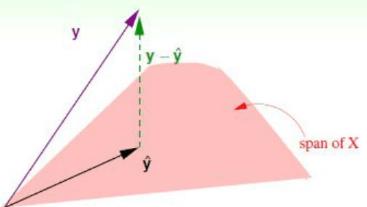
因为y^是x的线性组合而成，那么y^=span(x),（其中span表示由x生成的意思）。即y^和x在同一平面上，实际的y和y^是有差距的，用y−y^表示，即图中的绿线，从上图可以看出，y^其实就相当于y在x张成的平面所做的投影，即：y^=H⋅y.

对应的，若考虑(y−y^)，即相当于(I−H)y，类比上面的思想，我们也可以得到相同的结论，即(y−y^)相当于y以(I−H)所做的投影。由于实际数据D是有噪声的，考虑噪声的加入，修正y=noise+f(x)，其对应的图形化描述如下图：



和上面图片不同的地方在于加了noise（noise不在平面上的原因，个人认为是如果在平面上，那么完全可以用x来表示，那么也就不存在噪声了），那么从图中可以看出，我们可以假设(y−y^)为点到平面X的距离，那么同样这个距离也可以用noise来表示， 即noise(I−H)。分析到这里，最开始的式子可以改写为：

Ein¯=1N||(I−H)y)||2

=1N||(I−H)⋅noise)||2

=1N||(I−H)||2⋅||noise)||2

=1Ntrace(I−H)⋅||noise)||2

=1N[trace(I)−trace(H)]⋅||noise)||2

=1N[N−trace((x(xTx)−1)xT)]⋅||noise)||2

=1N[N−trace((xTx(xTx)−1))]⋅||noise)||2

=1N[N−(d+1)]⋅||noise)||2

=noise level⋅(1−d+1N)

也就得出了最开始写出的式子，类似的也可以写出Eout¯=noise level⋅(1+d+1N)

=>Eout¯−Ein¯=2(d+1)N，其对应的结果如下图：



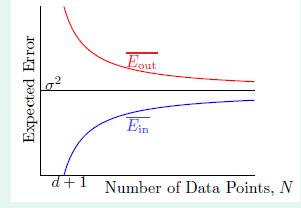
即N→∞时，Eout¯≈Ein¯=σ2,由此也就证明了上节课的求解是机器学习，因为它使得Eout(WLIN)足够小。

9-4：Linear Regression for Binary Classification

线性回归作二分类

之前作线性分类的时候，如果数据D中存在noise，即数据不是线性可分的时候，假设h(x)=sign(wTx)，首先这是一个NP-hard问题，没有什么特别好的求解算法，第二节介绍了pocket算法来求解，在这节内容里，我们学习了LinReg（线性回归）,即h(x)=wTx，观察两个结果发现有很相似的地方，那么有一个想法就是能不能直接使用回归求出的WLIN，然后直接得到g,也即：g(x)=sign(WTLIN⋅x),我们首先考察一下两种方法的错误：

pocket中错误用err0/1=[sign(wTx≠y)],LinReg中错误用errsqr=(wTx−y)2，其最终结果如图所示：



从图中可以发现，err0/1<errsqr总是成立的，由第七节VC限制理论，得到Eout≤err0/1+Ω

≤errsqr+Ω (其中Ω是模型复杂度)

本来err0/1就已经上限宽松了，若用errsqr，那么VC上限将更加宽松，说明g(x)=sign(WTLIN⋅x)不适合。

但是我们也可以使用WLIN，我们可以将它作为pocket算法的初始化值，这样子算法的收敛程度就会大大加快，另外一方面，因为WLIN是解析解求出的，求出来也很容易。