POJ 3155 Hard Life(最小割 最大密度子图)
2017-09-21 20:20
459 查看
Description
John is a Chief Executive Officer at a privately owned medium size company. The owner of the company has decided to make his son Scott a manager in the company. John fears that the owner will ultimately give CEO position to Scott
if he does well on his new manager position, so he decided to make Scott’s life as hard as possible by carefully selecting the team he is going to manage in the company.
John knows which pairs of his people work poorly in the same team. John introduced a
hardness factor of a team — it is a number of pairs of people from this team who work poorly in the same team divided by the total number of people in the team. The larger is the hardness factor, the harder is this team to manage. John wants to find
a group of people in the company that are hardest to manage and make it Scott’s team. Please, help him.
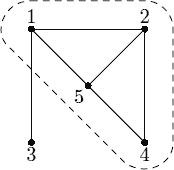
In the example on the picture the hardest team consists of people 1, 2, 4, and 5. Among 4 of them 5 pairs work poorly in the same team, thus hardness factor is equal to
5⁄4. If we add person number 3 to the team then hardness factor decreases to
6⁄5.
Input
The first line of the input file contains two integer numbers
n and m (1 ≤ n ≤ 100, 0 ≤ m ≤ 1000). Here
n is a total number of people in the company (people are numbered from 1 to
n), and m is the number of pairs of people who work poorly in the same team. Next
m lines describe those pairs with two integer numbers ai and
bi (1 ≤ ai, bi ≤
n, ai ≠ bi) on a line. The order of people in a pair is arbitrary and no pair is listed twice.
Output
Write to the output file an integer number k (1 ≤
k ≤ n) — the number of people in the hardest team, followed by
k lines listing people from this team in ascending order. If there are multiple teams with the same hardness factor then write any one.
Sample Input
Sample Output
Hint
Note, that in the last example any team has hardness factor of zero, and any non-empty list of people is a valid answer.
题目大意:求最大密度子图。
看了胡伯涛的《最小割模型在信息学竞赛中的应用》一文才来刷的这道题,很巧妙的问题转化。在原文中作者给出了两种建图的思路,都是先猜想一个答案,通过二分逼近,上限为 m,下限为 1/n ,该模型还可向带边权点权的图转化,后面刷到了相关题目在做说明吧:
(1) 第一种复杂度O(logn*maxflow(n+m,n+m));
保留原图所有点,对于每条边 (u,v) 另开一个新的节点 ei (点权为1),建容量为 INF 的有向边 (ei,u)、(ei,v) 。原图中每个点的点权设为 -g ,则转化为最大权闭合子图问题,从源点 s 向每个 ei 建一条容量为1的有向边 (s,ei),从原图中每个点向汇点
t 建一条容量为 g 的有向边 (v,t)。m - maxflow() 即为最大点权和,eps 定为了1e-8。
代码:
(2) 第二种O(logn*maxflow(n,n+m)
具体算法推导过程详见原文,这里只写一下建图的步骤,这种建图方法与上一种相比少了不少边。
源点 s 向每个原图中的点建一条容量为 U 的有向边 (s,v),原图中的边 (u,v),改建为两条容量为1的有向边 (u,v)、(v,u)。原图中每个点向汇点 t 建一条容量为 U+2*g-di的有向边 (v,t)(di为原图中每个点的度数),最小割保证了密度最大化。
代码:
John is a Chief Executive Officer at a privately owned medium size company. The owner of the company has decided to make his son Scott a manager in the company. John fears that the owner will ultimately give CEO position to Scott
if he does well on his new manager position, so he decided to make Scott’s life as hard as possible by carefully selecting the team he is going to manage in the company.
John knows which pairs of his people work poorly in the same team. John introduced a
hardness factor of a team — it is a number of pairs of people from this team who work poorly in the same team divided by the total number of people in the team. The larger is the hardness factor, the harder is this team to manage. John wants to find
a group of people in the company that are hardest to manage and make it Scott’s team. Please, help him.

In the example on the picture the hardest team consists of people 1, 2, 4, and 5. Among 4 of them 5 pairs work poorly in the same team, thus hardness factor is equal to
5⁄4. If we add person number 3 to the team then hardness factor decreases to
6⁄5.
Input
The first line of the input file contains two integer numbers
n and m (1 ≤ n ≤ 100, 0 ≤ m ≤ 1000). Here
n is a total number of people in the company (people are numbered from 1 to
n), and m is the number of pairs of people who work poorly in the same team. Next
m lines describe those pairs with two integer numbers ai and
bi (1 ≤ ai, bi ≤
n, ai ≠ bi) on a line. The order of people in a pair is arbitrary and no pair is listed twice.
Output
Write to the output file an integer number k (1 ≤
k ≤ n) — the number of people in the hardest team, followed by
k lines listing people from this team in ascending order. If there are multiple teams with the same hardness factor then write any one.
Sample Input
sample input #1 5 6 1 5 5 4 4 2 2 5 1 2 3 1 sample input #2 4 0
Sample Output
sample output #1 4 1 2 4 5 sample output #2 1 1
Hint
Note, that in the last example any team has hardness factor of zero, and any non-empty list of people is a valid answer.
题目大意:求最大密度子图。
看了胡伯涛的《最小割模型在信息学竞赛中的应用》一文才来刷的这道题,很巧妙的问题转化。在原文中作者给出了两种建图的思路,都是先猜想一个答案,通过二分逼近,上限为 m,下限为 1/n ,该模型还可向带边权点权的图转化,后面刷到了相关题目在做说明吧:
(1) 第一种复杂度O(logn*maxflow(n+m,n+m));
保留原图所有点,对于每条边 (u,v) 另开一个新的节点 ei (点权为1),建容量为 INF 的有向边 (ei,u)、(ei,v) 。原图中每个点的点权设为 -g ,则转化为最大权闭合子图问题,从源点 s 向每个 ei 建一条容量为1的有向边 (s,ei),从原图中每个点向汇点
t 建一条容量为 g 的有向边 (v,t)。m - maxflow() 即为最大点权和,eps 定为了1e-8。
代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cmath>
#include<vector>
using namespace std;
typedef struct node
{
int from,to;
double cap,flow;
node(int f = 0,int t = 0,double c = 0,double ff = 0):from(f),to(t),cap(c),flow(ff){}
}node;
const double INF = 1e5;
const int maxn = 8 * 1e3 + 5;
const double eps = 1e-8;
double Min(double a,double b)
{
return a < b ? a : b;
}
int n,m,s,t,sum;
vector<node> E;
node edge[maxn];
vector<int> G[maxn];
int cur[maxn],di[maxn],in[maxn];
bool vis[maxn];
void addedge(int from,int to,double cap,double flow)
{
E.push_back(node(from,to,cap,0));
E.push_back(node(to,from,0,0));
int mm = E.size();
G[from].push_back(mm-2);
G[to].push_back(mm-1);
}
bool BFS()
{
int x;
memset(vis,false,sizeof(vis));
queue<int> q;
q.push(s);
vis[s] = true;
di[s] = 0;
while(!q.empty())
{
x = q.front();
q.pop();
for(int i = 0;i < G[x].size(); ++i)
{
node &e = edge[G[x][i]];
if(e.cap > e.flow && !vis[e.to])
{
di[e.to] = di[x] + 1;
vis[e.to] = true;
q.push(e.to);
}
}
}
return vis[t];
}
double DFS(int x,double a)
{
double flow = 0,f;
if(x == t || a == 0) return a;
for(int &i = cur[x];i< G[x].size(); ++i)
{
node &e = edge[G[x][i]];
if(di[e.to] == di[x] + 1 && (f = DFS(e.to,Min(a,e.cap - e.flow))) > 0)
{
e.flow += f;
edge[G[x][i]^1].flow -= f;
flow += f;
a -= f;
if(a == 0) break;
}
}
return flow;
}
double maxflow()
{
double flow = 0;
while(BFS())
{
memset(cur,0,sizeof(cur));
flow += DFS(s,INF);
}
return flow;
}
void dfs(int x)
{
int len = G[x].size();
for(int i = 0;i < len; ++i)
{
node e = edge[G[x][i]];
if(!vis[e.to] && e.cap == e.flow)
{
vis[e.to] = true;
dfs(e.to);
}
}
}
void Solve()
{
int len = E.size();
double l = 1.0 / n,r = (double)m;
double mid,limit = 1.0 / n / n;
while(r - l > limit)
{
mid = (l + r) / 2.0;
for(int i = 0;i < len; ++i)
{
edge[i] = E[i];
if(edge[i].to == t) edge[i].cap = mid;
}
double temp = (double)m - maxflow();
if(temp > eps) l = mid;
else r = mid;
}
memset(vis,false,sizeof(vis));
for(int i = 0;i < len; ++i)
{
edge[i] = E[i];
if(edge[i].to == t) edge[i].cap = l;
}
maxflow();
vis[s] = true;
dfs(s);
sum = 0;
for(int i = 1;i <= n; ++i) if(vis[i]) ++sum;
if(sum)
{
printf("%d\n",sum);
for(int i = 1;i <= n; ++i) if(vis[i]) printf("%d\n",i);
}
else printf("1\n1\n");
}
int main()
{
int x,y;
s = 0,t = 8000;
scanf("%d %d",&n,&m);
memset(in,0,sizeof(in));
for(int i = 1;i <= m; ++i)
{
scanf("%d %d",&x,&y);
addedge(i + 100,x,INF,0);
addedge(i + 100,y,INF,0);
addedge(s,i + 100,1,0);
}
for(int i = 1;i <= n; ++i) addedge(i,t,0,0);
Solve();
return 0;
}(2) 第二种O(logn*maxflow(n,n+m)
具体算法推导过程详见原文,这里只写一下建图的步骤,这种建图方法与上一种相比少了不少边。
源点 s 向每个原图中的点建一条容量为 U 的有向边 (s,v),原图中的边 (u,v),改建为两条容量为1的有向边 (u,v)、(v,u)。原图中每个点向汇点 t 建一条容量为 U+2*g-di的有向边 (v,t)(di为原图中每个点的度数),最小割保证了密度最大化。
代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cmath>
#include<vector>
using namespace std;
typedef struct node
{
int from,to;
double cap,flow;
node(int f = 0,int t = 0,double c = 0,double ff = 0):from(f),to(t),cap(c),flow(ff){}
}node;
double INF;
const int maxn = 1e3 + 5;
const double eps = 1e-8;
double Min(double a,double b)
{
return a < b ? a : b;
}
int n,m,s,t,sum;
vector<node> E;
node edge[maxn * 5];
vector<int> G[maxn];
int cur[maxn * 5],di[maxn],in[maxn];
bool vis[maxn];
void addedge(int from,int to,double cap,double flow)
{
E.push_back(node(from,to,cap,0));
E.push_back(node(to,from,0,0));
int mm = E.size();
G[from].push_back(mm-2);
G[to].push_back(mm-1);
}
bool BFS()
{
int x;
memset(vis,false,sizeof(vis));
queue<int> q;
q.push(s);
vis[s] = true;
di[s] = 0;
while(!q.empty())
{
x = q.front();
q.pop();
for(int i = 0;i < G[x].size(); ++i)
{
node &e = edge[G[x][i]];
if(e.cap > e.flow && !vis[e.to])
{
di[e.to] = di[x] + 1;
vis[e.to] = true;
q.push(e.to);
}
}
}
return vis[t];
}
double DFS(int x,double a)
{
double flow = 0,f;
if(x == t || a == 0) return a;
for(int &i = cur[x];i< G[x].size(); ++i)
{
node &e = edge[G[x][i]];
if(di[e.to] == di[x] + 1 && (f = DFS(e.to,Min(a,e.cap - e.flow))) > 0)
{
e.flow += f;
edge[G[x][i]^1].flow -= f;
flow += f;
a -= f;
if(a == 0) break;
}
}
return flow;
}
double maxflow()
{
double flow = 0;
while(BFS())
{
memset(cur,0,sizeof(cur));
flow += DFS(s,INF);
}
return flow;
}
void dfs(int x)
{
int len = G[x].size();
for(int i = 0;i < len; ++i)
{
node e = edge[G[x][i]];
if(!vis[e.to] && e.cap > e.flow)
{
vis[e.to] = true;
dfs(e.to);
}
}
}
void Solve()
{
int len = E.size();
double l = 1.0 / n,r = (double)m;
double mid,limit = 1.0 / n / n;
while(r - l > limit)
{
mid = (l + r) / 2.0;
for(int i = 0;i < 2 * m; ++i) edge[i] = E[i];
for(int i = 2 * m;i < len; ++i)
{
edge[i] = E[i];
if(edge[i].to == t) edge[i].cap += 2 * mid;
}
double temp = (double)n * INF - maxflow();
if(temp > eps) l = mid;
else r = mid;
}
memset(vis,false,sizeof(vis));
for(int i = 0;i < 2 * m; ++i) edge[i] = E[i];
for(int i = 2 * m;i < len; ++i)
{
edge[i] = E[i];
if(edge[i].to == t) edge[i].cap += 2 * (l);
}
maxflow();
dfs(s);
vis[s] = true;
sum = 0;
for(int i = 1;i <= n; ++i) if(vis[i]) ++sum;
if(sum)
{
printf("%d\n",sum);
for(int i = 1;i <= n; ++i) if(vis[i]) printf("%d\n",i);
}
else printf("1\n1\n");
}
int main()
{
int x,y;
s = 0,t = 101;
scanf("%d %d",&n,&m);
INF = (double)m;
memset(in,0,sizeof(in));
for(int i = 0;i < m; ++i)
{
scanf("%d %d",&x,&y);
addedge(x,y,1,0);
addedge(y,x,1,0);
in[x]++,in[y]++;
}
for(int i = 1;i <= n; ++i)
{
addedge(s,i,INF,0);
addedge(i,t,INF - (double)in[i],0);
}
Solve();
return 0;
}
相关文章推荐
- POJ-3155-Hard Life(最大密度子图)(01分数规划+最小割)
- 【POJ】3155 Hard Life 最大密度子图
- poj 3155 Hard Life(01分数规划+最大流--最大密度子图)
- POJ 3155 Hard Life(最大密度子图)
- POJ 3155 Hard Life(最大密度子图)
- poj 3155(Hard Life)分数规划/最大密度子图
- POJ 3155 Hard Life 最大密度子图
- POJ 3155 Hard Life(最小割-最大密集子图)
- POJ 3155 Hard Life(最大密度子图)
- POJ 3155 Hard Life(最大密度子图)
- POJ 3155 Hard Life(最大密度子图)
- poj 3155 Hard Life(最大密度子图,01分数规划)
- poj 3155 Hard Life 最大密度子图
- POJ 3155 最大密度子图 二分+最小割
- poj 3155 Hard Life 【最大密度子图】 【0-1分数规划 + 最小割】
- POJ 3155 Hard Life 最大密度子图
- poj 3155 Hard Life 最大密度子图
- poj 3155 Hard Life (最大密度子图)
- POJ 3155 Hard Life 最大密度子图
- poj 3155 Hard Life 最大密度子图
