论文信息

1 Introduction

　　本文提出了 DIFFPOOL，一个可微的图池化模块，可以以分层和端到端的方式适应各种图神经网络架构。

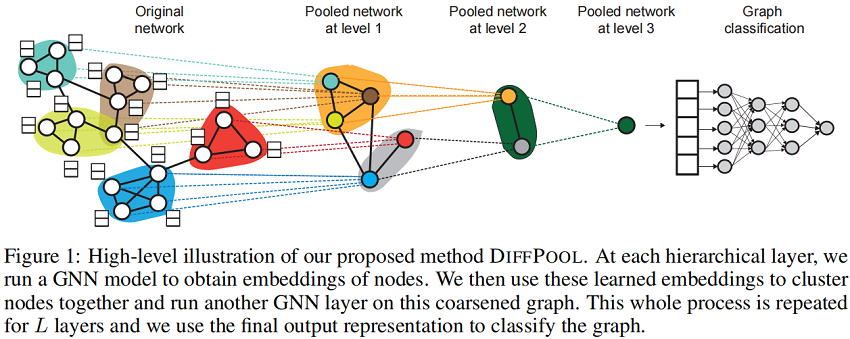
2 Method

2.1  Pooling with an assignment matrix

　　第 $l$ 层的聚类分配矩阵 $S^{(l)} \in \mathbb{R}^{n_{l} \times n_{l+1}} $。其中，$S^{(l)} $ 的每一行对应第 $l$ 层的 $n_l$ 个节点（或簇）之一 ，$S^{(l)}$ 的每一列对应 $l+1$ 层的 $n_{l+1}$ 簇之一。

　　DIFFPOOL  可以表达为 $\left(A^{(l+1)}, X^{(l+1)}\right)=\operatorname{DiFF} \operatorname{POOL}\left(A^{(l)}, Z^{(l)}\right)$ ，即根据当前邻接矩阵 $A^{(l)}$ 和节点嵌入矩阵 $Z^{(l)}$ 可以生成一个新的粗化邻接矩阵 $A^{(l+1)}$ 和一个新的嵌入矩阵 $X^{(l+1)}$。并应用以下两个方程式：

　　　　$\begin{array}{l}{\large X^{(l+1)}=S^{(l)^{T}} Z^{(l)} \in \mathbb{R}^{n_{l+1} \times d} } \quad\quad\quad(3) \\{\large A^{(l+1)}=S^{(l)^{T}} A^{(l)} S^{(l)} \in \mathbb{R}^{n_{l+1} \times n_{l+1}}}  \quad\quad\quad(4) \end{array}$

　　其中，

• [li]$A^{(l+1)}$ 代表着实数矩阵，$A_{i j}^{(l+1)}$ 可以看作是集群 $i$ 和簇 $j$ 之间的连通性强度；
• $X^{(l+1)}$ 的第 $i$ 行对应于簇 $i$ 的嵌入；

2.2 Learning the assignment matrix

　　嵌入矩阵：

　　　　$Z^{(l)}=\operatorname{GNN}_{l, \text { embed }}\left(A^{(l)}, X^{(l)}\right)   \quad\quad\quad(5)$

 　　分配矩阵：

　　　　$S^{(l)}=\operatorname{softmax}\left(\operatorname{GNN}_{l, \text { pool }}\left(A^{(l)}, X^{(l)}\right)\right)  \quad\quad\quad(6)$

　　总结：Embedding GNN 为这一层的输入节点生成新的嵌入，而 pooling GNN 生成输入节点对 $n_{l+1}$ 簇的概率分配。

　　在第 $l=0$ 层的 $\text{Eq.5}$ 和 $\text{Eq.6}$ 的输入是原始图的邻接矩阵 $A$ 和节点特征矩阵 $F$。在 GNN 模型的倒数第二层 $L−1$，我们将分配矩阵 $S^{(L-1)} $ 设置为 $1$ 的向量，即将最后一层 $L$ 的所有节点分配给一个簇，生成与整个图对应的最终嵌入向量。最终的输出嵌入可以作为可微分类器(例如，softmax )的特征输入，整个系统可以使用随机梯度下降进行端到端训练。

2.3 Auxiliary Link Prediction Objective and Entropy Regularization

　　实际上，$\text{Eq.4}$ 很难通过梯度进行训练（计算太复杂）。为了缓解这个问题，我们用一个辅助 link prediction 目标训练 pooling GNN ，该目标编码了附近节点应该汇集在一起的直觉。在每一层 $l$，我们最小化 $L_{\mathrm{LP}}=\left\|A^{(l)}, S^{(l)} S^{(l)^{T}}\right\|_{F}$，其中 $\|\cdot\|_{F}$ 表示 Frobenius 范数。

　　需要注意的是，随着层数变深，$A^{l}$ 可以认为是基于 low level 的聚类分配矩阵的函数。

　　pooling GNN 每个节点的输出簇分配通常应该接近一个 one-hot 向量，以便明确定义每个簇或子图的隶属关系。因此，我们通过最小化来规范簇分配的熵

　　　　$L_{\mathrm{E}}=\frac{1}{n} \sum\limits _{i=1}^{n} H\left(S_{i}\right) $

　　其中，$H$ 为熵函数，$S_{i}$ 为 $S$ 的第 $i$ 行。

　　在训练过程中，将每层的 $L_{LP} $ 和 $L_{E}$ 添加到分类损失中。在实践中，我们观察到，使用侧目标的训练需要更长的时间来收敛，但仍然取得了更好的性能和更多可解释的聚类分配。

3 Experiments

数据集

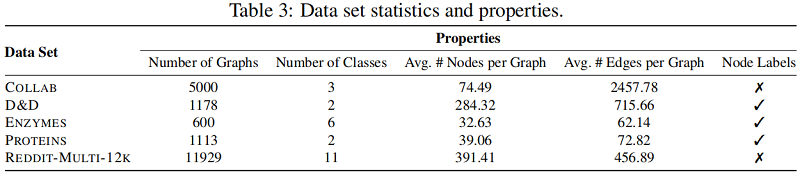
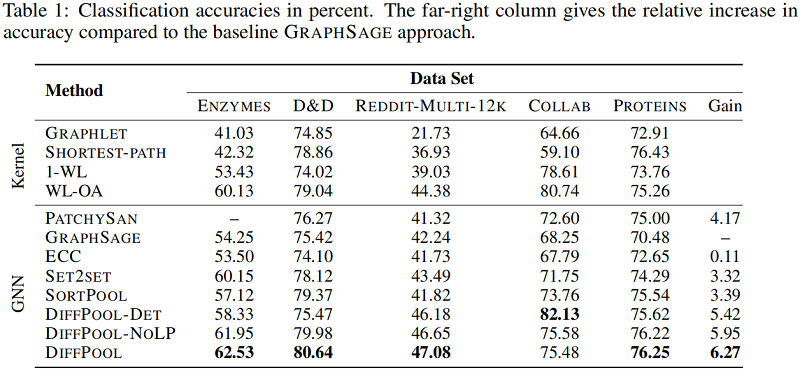
图分类

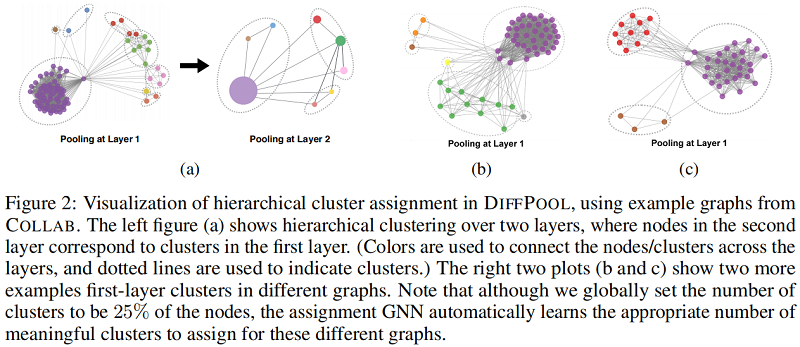
聚类分配分析

4 Conclusion

　　我们介绍了一种可微池化的gnn方法，它能够提取真实世界图的复杂层次结构。通过将所提出的池化层结合现有的GNN模型，我们在几个图分类基准上获得了新的最先进的结果。有趣的未来发展方向包括学习硬聚类分配，以进一步降低更高层次的计算成本，同时确保可微性，并将分层池化方法应用于其他需要对整个图结构进行建模的下游任务。