【线性代数】矩阵、向量、行列式、特征值与特征向量(掌握这些概念一篇文章就够了)
2017-08-25 19:55
921 查看
在数学领域中,线性代数是一门十分有魅力的学科,首先,它不难学;其次,它能广泛应用于现实生活中;另外,在机器学习越来越被重视的现在,线性代数也能算得上是一个优秀程序员的基本素养吧?
{2x−4x−+y2y==00(1)
⎧⎩⎨2xxx+−+3yy2y++−z2zz===6−15
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪a11x1a21x1a31x1am1x1++++a12x2a22x2a32x2am2x2++++⋯⋯⋯⋮⋯+a1nxn+a2nxn+a3nxn+amnxn====b1b2b3bm
看到这样子的方程组,不由感到十分怀念。不过有没有这种感想,当年解三元一次方程组的时候,特别烦,消元后要抄一遍,代入后又抄一遍,特别麻烦。于是数学家发明了矩阵,把方程组中所有系数写到了一个框里面,把所有未知数写到第二个框里,把所有等式右边的值写到第三个框里。
⎡⎣⎢⎢⎢⎢⎢⎢⎢a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋯a1na2na3n⋮amn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢⎢⎢x1x2x3⋮xn⎤⎦⎥⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢⎢b1b2b3⋮bm⎤⎦⎥⎥⎥⎥⎥⎥⎥(2)
比如方程组 (1) 也可表示为:
[2−4−12][x1x2]=[00]
观察 (2) 式不难发现,复杂的方程组用矩阵表示后,还是很复杂,所以可以把 (2) 式更加简洁地表示成增广矩阵:
⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋯a1na2na3n⋮amnb1b2b3bm⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥
同理,比如方程组 (1) 也可表示为增广矩阵:
[2−4−1200](3)
特别地,当方程组的等式右边全为0,即bi=0,其中i=1,2,3…n时,方程组为齐次线性方程组,增广矩阵可直接表示成系数矩阵。比如增广矩阵 (3) 可直接表示成:
[2−4−12]
我们称,方程组的等式右边全为0的方程组为齐次线性方程组,否则为非齐次线性方程组。
来回顾一下这个方程组:
{2x−4x−+y2y==00(1)
等式右边全为0,所以把这个方程组写成矩阵形式:
A=[2−4−12]
要解这个方程组,当然使用消元法,不同于中学的是直接在矩阵里面消元:
[2−4−12]“第一行的2倍加到第二行,得”−−−−−−−−−−−−−−−−−−−−[20−10]
看到消元后的新矩阵是不是觉得很直观,如果你你把新矩阵还原成方程组的形式,有:
{2x0x−+y0y==00⇒2x−y=0
仔细观察可发现,原本有两个式子的方程组经过消元后,变成了只有一个方程组。这种情况在中学时,无论做多少题都不会遇到的,因为在中学里,学的初等数学方程组都是有唯一解的。而在线性代数中,我们把这种情况成为方程组系数矩阵的秩为1,记为r(A)=1。当矩阵的秩小于未知数的个数时,方程组有无数个解;当矩阵的秩等于未知数的个数时,方程组只有零解。
由于方程组(1)有两个未知数,而r(A)=1<2,所以方程组(1)有无数个解。设 y=2 ,则 x=1;再设 k 为任意常数,则 x=k, y=2k 为方程组(1)的解,写成矩阵的形式为:
[2−4−12][1k2k]=[00]
(其中,[12]称为方程组(1)的基础解系)
(2)非齐次线性方程组
再来看一个3个未知数的方程组:
⎧⎩⎨2xxx+−+3yy2y++−z2zz===6−15
右边等式不为0,改写成增广矩阵:
[Ab]=⎡⎣⎢⎢2113−1212−16−15⎤⎦⎥⎥
同理,对 [ A | b] 进行初等行变换(即消元):
[Ab]→⎡⎣⎢⎢121−13221−1−165⎤⎦⎥⎥→⎡⎣⎢⎢100−1532−3−3−186⎤⎦⎥⎥→⎡⎣⎢⎢100−15152−3−15−1818⎤⎦⎥⎥→⎡⎣⎢⎢100−1502−3−6−186⎤⎦⎥⎥
这一次进行初等行变换后,对于任意的非齐次线性方程组,当 r(A)=r(A|b)=未知数的个数 时,非齐次线性方程组有唯一解;当 r(A)=r(A|b)<未知数的个数 时,非齐次线性方程组有无数个解;当 r(A) 不等于 r(A|b) 时,非齐次线性方程组无解。
可见 r(A)=r(A|b)=3,所以[A|b]有唯一解,写回方程组形式:
⎧⎩⎨x00−++y5y0+−−2z3z6z===−186
解得唯一解为:⎡⎣⎢−4−11⎤⎦⎥,也可以写成矩阵的转置:[−4−11]T
有这么一个矩阵:⎡⎣⎢⎢⎢⎢⎢⎢⎢a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋯a1na2na3n⋮amn⎤⎦⎥⎥⎥⎥⎥⎥⎥,
将矩阵按列分块:⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋯a1na2na3n⋮amn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥
随便选一列出来,假设选第i列⎡⎣⎢⎢⎢⎢⎢⎢⎢a1ia2ia3i⋮ami⎤⎦⎥⎥⎥⎥⎥⎥⎥出来
假设给第1列一个头衔为α1;
同理给第2列一个头衔为α2;
⋯
同理给第n列一个头衔为αn;
那么,
α1=[a11a21a31⋯am1]T
α2=[a12a22a32⋯am2]T
⋯
αm=[a1na2na3n⋯amn]T
可见,
原矩阵中的第 i 列只要用 αi 表示即可。这个小小的 αi,我们称之为列向量。
原矩阵共有 m 行,则向量 αi 中有 m 个分量(元素),也叫做 m 维向量。
用 n 个 m 维向量来表示原矩阵:
A=[α1α2α3⋯αm]
另外,矩阵A中把 α1, α2, α3, … , αm 多个向量称为向量组。
同理,我们对矩阵A按行分块,并对每行元素用向量表示。
α1=[a11a12a13⋯a1n]
α2=[a21a22a23⋯a2n]
⋯
αm=[am1am2am3⋯amn]
可见,
原矩阵中的第 i 行只要用 αi 表示即可。这个小小的 αi,我们称之为行向量。
原矩阵共有 n 列,则向量 αi 中有 n 个分量(元素),也叫做 n 维向量。
用 α1, α2, α3, … , αn 向量组来表示原矩阵:
A=⎡⎣⎢⎢⎢⎢⎢⎢α1α2α3⋯αn⎤⎦⎥⎥⎥⎥⎥⎥
显然,用向量组便可轻松对矩阵瘦身。
假设有这么一个矩阵
A=[2−4−12]
我们对其按行分块,则有向量:
α1=[2−1]
α2=[−42]
如果用行向量 α1, α2, α3, … , αn 来表示的矩阵A经过初等行变换后,某行(即某个向量αi)的元素全变为0,那么则称 α1, α2, α3, … , αn 向量组线性相关(可以理解为多个向量间或系数矩阵有线性关系)。
如果齐次线性方程组的系数矩阵有线性关系,那么齐次线性方程组有无穷多个解。为了看清楚 α1, α2, α3, … , αn 是否线性相关,对矩阵A进行初等行变换后,发现:
[20−10]
所以, α1, α2, α3, … , αn 向量组线性相关。
(2)线性无关
假设有这么一个矩阵
A=⎡⎣⎢121−13221−1⎤⎦⎥
我们对其按行分块,则有向量:
α1=[1−12]
α1=[231]
α1=[12−1]
如果用行向量 α1, α2, α3, … , αn 来表示的矩阵A经过初等行变换后,某行(即某个向量αi)的元素不全为0,那么则称 α1, α2, α3, … , αn 向量组线性无关。
为了看清楚 α1, α2, α3, … , αn 是否线性无关,对矩阵A进行初等行变换后,发现:
⎡⎣⎢100−1502−3−6⎤⎦⎥
所以, α1, α2, α3, … , αn 向量组线性无关。
在笛卡尔直角坐标体系中,向量(1,0), (0,1)分别代表了横坐标轴、纵坐标轴,对这两个向量线性组合的整体就可以表示出一个平面,即2维向量空间;向量(1,0,0), (0,1,0), (0,0,1)分别代表了x坐标轴、y坐标轴、z坐标轴,对这三个向量线性组合表示出的整体可表示出一个3维向量空间;以此类推。
有规律的是,n 维向量空间中的 n个坐标轴向量是互相垂直的(就算是4维空间的4个坐标轴也是垂直的,只不过我们处于三维中,难以感知到四维空间,只能想象)。我们称向量间的垂直为正交。数学家对向量空间更是大开脑洞,认为不一定是笛卡尔体系的(1,0,0), (0,1,0), (0,0,1)才能是坐标轴,只要是线性无关的向量组中的n个向量都可以当做是n维向量空间中的坐标轴,相当于将笛卡尔坐标体系的原点固定住,将所有坐标轴就像陀螺一样旋转某个角度,得出的新坐标轴肯定是线性无关的。
“n个向量组成的线性无关向量组,在n维向量空间中,可充当坐标轴。”这就是线性代数的向量空间的核心思想。
行列式的本质是什么?柯西给出了答案。
假设在一个平面中有两个向量:
x1=(a, c), x2=(b, d);
x1与横坐标的角度为α,x2与横坐标的角度为β;
x1的模为 ||x1||,x2的模为 ||x2||;
如图:
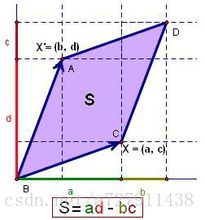
我们要求图中的 S,即向量平移后端点相交而围成的平行四边形的面积:
S = ||x1|| · ||x2|| · sin(β-α)
= ||x1|| · ||x2|| · (sinβcosα - cosβsinα)
= ad - bc
对 x1 和 x2 向量类似行向量那样子对元素命名:
x1=(a11, a12)
x2=(a21, a22)
重新得到 S = a11 · a22 - a12 · a21,
数学家对向量 x1 和 x2 写成行列式,代表了 S 的值:
S=∣∣∣a11a21a12a22∣∣∣
行列式不过就是将矩阵的括号改成了两条竖线,用竖线包着的元素,最终可以算出一个数,这个数就是行列式,行列式就是一个数,这个数是不同行不同列元素乘积的代数和。而矩阵本质为表格或数组,这是两者不同之处。
如果继续推,可以推出:在二维空间,行列式是面积;在三维空间,行列式是体积;在高维空间,行列式是一个数。换句话说,就是由n个向量组成的线性无关向量组,可以表示成行列式,并且算出的结果肯定不为0。以次可推,由n个向量组成的线性相关向量组表示成的行列式值为0。
设 A 是 n 阶矩阵,如果存在一个数 λ 及非零的 n 维列向量 α ,使得
Aα=λα
成立,则称 λ 是矩阵 A 的一个特征值,称非零向量 α 是矩阵 A 属于特征值 λ 的一个特征向量。
观察这个定义可以发现,特征值是一个数,特征向量是一个列向量,一个矩阵乘以一个向量就等于一个数乘以一个向量。这个定义感觉太抽象了,我们来举一个具体的例子:
设 A 是 3 阶矩阵,
A=⎡⎣⎢11−31−21−123⎤⎦⎥
存在一个数 λ ,
λ=4
且存在一个非零的 3 维列向量 α ,
α=⎡⎣⎢−4517⎤⎦⎥
使得 Aα = λα,即
⎡⎣⎢11−31−21−123⎤⎦⎥⎡⎣⎢−4517⎤⎦⎥=4⎡⎣⎢−4517⎤⎦⎥(4)
则称 λ=4 为矩阵A的特征值,
(为了方便,简称 4 为特征值)
也称 α=[ -4, 5, 17 ]T 是矩阵A属于特征值为 4 的一个特征向量。
(为了方便,简称 [ -4, 5, 17 ]T 为特征向量)
对于上面的(4)式,我们可以把它还原为方程组验证此式是否成立,还原过程如下:
⎡⎣⎢⎢11−31−21−123⎤⎦⎥⎥⎡⎣⎢(−4)(5)(17)⎤⎦⎥=4⎡⎣⎢−4517⎤⎦⎥
⟹−4⎡⎣⎢11−3⎤⎦⎥+5⎡⎣⎢1−21⎤⎦⎥+17⎡⎣⎢−123⎤⎦⎥=4⎡⎣⎢−4517⎤⎦⎥
⟹⎧⎩⎨1×(−4)1×(−4)(−3)×(−4)+++1×5(−2)×51×5+++(−1)×172×173×17===4×(−4)4×54×17
⟹⎧⎩⎨−4−412+−+5105−++173451===−162068
显然,每个等式两边相等, Aα = λα 成立!(如果不知道为什么可以还原成方程组的话,请翻回到上面的非齐次方程组部分,可发现在这里 α 相当于解向量, λα 相当于 b 向量)
总的来说,一个n行n列的矩阵的特征值个数少于或等于 n 个。
还是以矩阵A为例,满足 Aα = λα 的式子有:
(1)
⎡⎣⎢11−31−21−123⎤⎦⎥⎡⎣⎢−4517⎤⎦⎥=4⎡⎣⎢−4517⎤⎦⎥
特征值 λ1 = 4,特征向量 α1 = [ -4 5 17 ]T。
(2)
⎡⎣⎢11−31−21−123⎤⎦⎥⎡⎣⎢111⎤⎦⎥=1⎡⎣⎢111⎤⎦⎥
特征值 λ2 = 1,特征向量 α2 = [ 1 1 1 ]T。
(3)
⎡⎣⎢11−31−21−123⎤⎦⎥⎡⎣⎢1−31⎤⎦⎥=−3⎡⎣⎢1−31⎤⎦⎥
特征值 λ3 = -3,特征向量 α3 = [ 1 -3 1 ]T。
另外,一个特征值对应的特征向量的个数也不一定只有一个。 (由于这句话会引申出特别多的性质,所以本文就不举这句话的例子了)
Aa=λα,α≠0
移项,
⟹λα−Aα=0
利用结合律,由于 λ 是一个数不能直接减矩阵A,所以给 λ 乘以一个单位矩阵E。假设E为2阶单位矩阵,E=(1001),即从左上角到右下角的对角线上的元素全为1,其余为0,
⟹(λE−A)α=0(5)
把(5)式中的矩阵(λE-A)看做是矩阵B,把a列向量看做是x解向量,那么Ax=0是一个齐次线性方程组,由于列向量x不等于0,所以这个齐次线性方程组没有零解,矩阵A每行当作列向量组成的向量组线性相关,于是根据上面行列式的结论,矩阵A写成行列式|A|后算出的结果为0,
⟹|λE−A|=0(6)
解(6)式即可解出多个 λ 值,如 λ1, λ2, λ3 … λn ,将 λi 值代回到(5)式,按照求解齐次线性方程组的方式,即可解出属于 λi 的非零特征向量 ai 。
⟹(λiE−A)a=0⟹αi=[a1,a2,...,an]T
由于本文对行列式介绍的篇幅太少,而求特征值与特征向量会涉及对行列式的计算,所以博主我就不举例子了(其实是懒)。
Aa=λα
对于特征值与特征向量,有许多不同的理解,我自己从网络上的观点总结了一下,大概分为三种理解:
第一种理解:从向量的角度来看,一个列向量在左乘一个矩阵后,会经过一系列的线性变换,最终向量的长度会变成原来的 λ 倍。
第二种理解:从矩阵的角度来看,矩阵是一种线性变化的描述,特征向量是一个不变的方向,特征值是线性变化的结果。
第三种理解:从向量空间的角度来看,因为不同特征值对应的特征向量线性无关,把每个特征向量看做是一个坐标轴,特征值是对应坐标轴(即特征向量)的坐标值。简单来说,就是用特征值(坐标)与特征向量(坐标轴)来表示原矩阵。
以上三种理解由浅入深,第三种理解才是本质的理解,但首先需要对向量空间有深刻的理解。
1、《麻省理工公开课:线性代数》
2、《可汗学院公开课:线性代数》
1、线代的入门:《如何生动有趣的入门线性代数》
2、线代的基础:《线性代数知识汇总》
3、线代的理解:《关于线性代数》
4、结合概率统计的线性回归算法:《机器学习之线性回归及代码示例》
5、主成分分析法(PCA)的原理:《一分钟理解 PCA 的原理》
6、PCA的简单解释:《浅解PCA》
7、PCA的通俗理解:《通俗理解PCA降维作用》
8、人脸识别之特征脸算法理论:《特征脸EigenFace与PCA》
9、特征脸的实战:《运用特征脸方法的基于Opencv的猫脸检测实现》
10、矩阵的md格式参考于:《使用LaTeX写矩阵》
转载请留言,原创于:http://blog.csdn.net/a727911438?viewmode=contents
一、线性代数的入门知识
很多人在大学学习线性代数时,国内教材书上大多一开始就是行列式的表示、计算、性质等等东西,让人看得云里雾里,一头雾水,然后要花很多时间才大概知道线性代数是个什么东西。本文不提书上晦涩难懂的内容,尽量用大白话来阐述我对线性代数的浅显理解。(一)矩阵
1、矩阵的表示
在中学的时候,我们会经常看到这样子的方程组:{2x−4x−+y2y==00(1)
⎧⎩⎨2xxx+−+3yy2y++−z2zz===6−15
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪a11x1a21x1a31x1am1x1++++a12x2a22x2a32x2am2x2++++⋯⋯⋯⋮⋯+a1nxn+a2nxn+a3nxn+amnxn====b1b2b3bm
看到这样子的方程组,不由感到十分怀念。不过有没有这种感想,当年解三元一次方程组的时候,特别烦,消元后要抄一遍,代入后又抄一遍,特别麻烦。于是数学家发明了矩阵,把方程组中所有系数写到了一个框里面,把所有未知数写到第二个框里,把所有等式右边的值写到第三个框里。
⎡⎣⎢⎢⎢⎢⎢⎢⎢a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋯a1na2na3n⋮amn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢⎢⎢x1x2x3⋮xn⎤⎦⎥⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢⎢b1b2b3⋮bm⎤⎦⎥⎥⎥⎥⎥⎥⎥(2)
比如方程组 (1) 也可表示为:
[2−4−12][x1x2]=[00]
观察 (2) 式不难发现,复杂的方程组用矩阵表示后,还是很复杂,所以可以把 (2) 式更加简洁地表示成增广矩阵:
⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋯a1na2na3n⋮amnb1b2b3bm⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥
同理,比如方程组 (1) 也可表示为增广矩阵:
[2−4−1200](3)
特别地,当方程组的等式右边全为0,即bi=0,其中i=1,2,3…n时,方程组为齐次线性方程组,增广矩阵可直接表示成系数矩阵。比如增广矩阵 (3) 可直接表示成:
[2−4−12]
我们称,方程组的等式右边全为0的方程组为齐次线性方程组,否则为非齐次线性方程组。
2、矩阵的解方程组
(1)齐次线性方程组来回顾一下这个方程组:
{2x−4x−+y2y==00(1)
等式右边全为0,所以把这个方程组写成矩阵形式:
A=[2−4−12]
要解这个方程组,当然使用消元法,不同于中学的是直接在矩阵里面消元:
[2−4−12]“第一行的2倍加到第二行,得”−−−−−−−−−−−−−−−−−−−−[20−10]
看到消元后的新矩阵是不是觉得很直观,如果你你把新矩阵还原成方程组的形式,有:
{2x0x−+y0y==00⇒2x−y=0
仔细观察可发现,原本有两个式子的方程组经过消元后,变成了只有一个方程组。这种情况在中学时,无论做多少题都不会遇到的,因为在中学里,学的初等数学方程组都是有唯一解的。而在线性代数中,我们把这种情况成为方程组系数矩阵的秩为1,记为r(A)=1。当矩阵的秩小于未知数的个数时,方程组有无数个解;当矩阵的秩等于未知数的个数时,方程组只有零解。
由于方程组(1)有两个未知数,而r(A)=1<2,所以方程组(1)有无数个解。设 y=2 ,则 x=1;再设 k 为任意常数,则 x=k, y=2k 为方程组(1)的解,写成矩阵的形式为:
[2−4−12][1k2k]=[00]
(其中,[12]称为方程组(1)的基础解系)
(2)非齐次线性方程组
再来看一个3个未知数的方程组:
⎧⎩⎨2xxx+−+3yy2y++−z2zz===6−15
右边等式不为0,改写成增广矩阵:
[Ab]=⎡⎣⎢⎢2113−1212−16−15⎤⎦⎥⎥
同理,对 [ A | b] 进行初等行变换(即消元):
[Ab]→⎡⎣⎢⎢121−13221−1−165⎤⎦⎥⎥→⎡⎣⎢⎢100−1532−3−3−186⎤⎦⎥⎥→⎡⎣⎢⎢100−15152−3−15−1818⎤⎦⎥⎥→⎡⎣⎢⎢100−1502−3−6−186⎤⎦⎥⎥
这一次进行初等行变换后,对于任意的非齐次线性方程组,当 r(A)=r(A|b)=未知数的个数 时,非齐次线性方程组有唯一解;当 r(A)=r(A|b)<未知数的个数 时,非齐次线性方程组有无数个解;当 r(A) 不等于 r(A|b) 时,非齐次线性方程组无解。
可见 r(A)=r(A|b)=3,所以[A|b]有唯一解,写回方程组形式:
⎧⎩⎨x00−++y5y0+−−2z3z6z===−186
解得唯一解为:⎡⎣⎢−4−11⎤⎦⎥,也可以写成矩阵的转置:[−4−11]T
(二)向量
中学时期学的向量是在笛卡尔直角坐标系下表示的向量。而在线性代数中,向量可以表示到三维以上,难以再以三维所见所得来理解向量,从而向量变得非常抽象。本文不涉及很多抽象概念,力求用大白话来理解和解释向量。1、列向量
可能是数学家觉得用矩阵来代表方程组还是太麻烦还废纸,所以又苦思冥想,最终想到了用向量再来继续简化矩阵,举个例子:有这么一个矩阵:⎡⎣⎢⎢⎢⎢⎢⎢⎢a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋯a1na2na3n⋮amn⎤⎦⎥⎥⎥⎥⎥⎥⎥,
将矩阵按列分块:⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋯a1na2na3n⋮amn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥
随便选一列出来,假设选第i列⎡⎣⎢⎢⎢⎢⎢⎢⎢a1ia2ia3i⋮ami⎤⎦⎥⎥⎥⎥⎥⎥⎥出来
假设给第1列一个头衔为α1;
同理给第2列一个头衔为α2;
⋯
同理给第n列一个头衔为αn;
那么,
α1=[a11a21a31⋯am1]T
α2=[a12a22a32⋯am2]T
⋯
αm=[a1na2na3n⋯amn]T
可见,
原矩阵中的第 i 列只要用 αi 表示即可。这个小小的 αi,我们称之为列向量。
原矩阵共有 m 行,则向量 αi 中有 m 个分量(元素),也叫做 m 维向量。
用 n 个 m 维向量来表示原矩阵:
A=[α1α2α3⋯αm]
另外,矩阵A中把 α1, α2, α3, … , αm 多个向量称为向量组。
3、行向量
有列向量,自然有行向量。同理,我们对矩阵A按行分块,并对每行元素用向量表示。
α1=[a11a12a13⋯a1n]
α2=[a21a22a23⋯a2n]
⋯
αm=[am1am2am3⋯amn]
可见,
原矩阵中的第 i 行只要用 αi 表示即可。这个小小的 αi,我们称之为行向量。
原矩阵共有 n 列,则向量 αi 中有 n 个分量(元素),也叫做 n 维向量。
用 α1, α2, α3, … , αn 向量组来表示原矩阵:
A=⎡⎣⎢⎢⎢⎢⎢⎢α1α2α3⋯αn⎤⎦⎥⎥⎥⎥⎥⎥
显然,用向量组便可轻松对矩阵瘦身。
3、线性相关与线性无关
(1)线性相关假设有这么一个矩阵
A=[2−4−12]
我们对其按行分块,则有向量:
α1=[2−1]
α2=[−42]
如果用行向量 α1, α2, α3, … , αn 来表示的矩阵A经过初等行变换后,某行(即某个向量αi)的元素全变为0,那么则称 α1, α2, α3, … , αn 向量组线性相关(可以理解为多个向量间或系数矩阵有线性关系)。
如果齐次线性方程组的系数矩阵有线性关系,那么齐次线性方程组有无穷多个解。为了看清楚 α1, α2, α3, … , αn 是否线性相关,对矩阵A进行初等行变换后,发现:
[20−10]
所以, α1, α2, α3, … , αn 向量组线性相关。
(2)线性无关
假设有这么一个矩阵
A=⎡⎣⎢121−13221−1⎤⎦⎥
我们对其按行分块,则有向量:
α1=[1−12]
α1=[231]
α1=[12−1]
如果用行向量 α1, α2, α3, … , αn 来表示的矩阵A经过初等行变换后,某行(即某个向量αi)的元素不全为0,那么则称 α1, α2, α3, … , αn 向量组线性无关。
为了看清楚 α1, α2, α3, … , αn 是否线性无关,对矩阵A进行初等行变换后,发现:
⎡⎣⎢100−1502−3−6⎤⎦⎥
所以, α1, α2, α3, … , αn 向量组线性无关。
4、向量空间
向量空间是线性代数中抽象的一部分,常用于物理研究中探索多维空间的奥秘(有没有用于物理中不太清楚,感觉的)。在笛卡尔直角坐标体系中,向量(1,0), (0,1)分别代表了横坐标轴、纵坐标轴,对这两个向量线性组合的整体就可以表示出一个平面,即2维向量空间;向量(1,0,0), (0,1,0), (0,0,1)分别代表了x坐标轴、y坐标轴、z坐标轴,对这三个向量线性组合表示出的整体可表示出一个3维向量空间;以此类推。
有规律的是,n 维向量空间中的 n个坐标轴向量是互相垂直的(就算是4维空间的4个坐标轴也是垂直的,只不过我们处于三维中,难以感知到四维空间,只能想象)。我们称向量间的垂直为正交。数学家对向量空间更是大开脑洞,认为不一定是笛卡尔体系的(1,0,0), (0,1,0), (0,0,1)才能是坐标轴,只要是线性无关的向量组中的n个向量都可以当做是n维向量空间中的坐标轴,相当于将笛卡尔坐标体系的原点固定住,将所有坐标轴就像陀螺一样旋转某个角度,得出的新坐标轴肯定是线性无关的。
“n个向量组成的线性无关向量组,在n维向量空间中,可充当坐标轴。”这就是线性代数的向量空间的核心思想。
(三)行列式
行列式作为国内各个教材书中的第一个章节的内容,证明了其在线性代数中的重要性。但是如果从教材中的行列式入手学习线性代数,那是要吃不少苦头的,因为只学了行列式,没有具备矩阵和向量的知识的情况下,很容易一脸懵逼。由于行列式涉及的概念、性质、计算众多,所以本文只简单介绍一下行列式。行列式的本质是什么?柯西给出了答案。
假设在一个平面中有两个向量:
x1=(a, c), x2=(b, d);
x1与横坐标的角度为α,x2与横坐标的角度为β;
x1的模为 ||x1||,x2的模为 ||x2||;
如图:

我们要求图中的 S,即向量平移后端点相交而围成的平行四边形的面积:
S = ||x1|| · ||x2|| · sin(β-α)
= ||x1|| · ||x2|| · (sinβcosα - cosβsinα)
= ad - bc
对 x1 和 x2 向量类似行向量那样子对元素命名:
x1=(a11, a12)
x2=(a21, a22)
重新得到 S = a11 · a22 - a12 · a21,
数学家对向量 x1 和 x2 写成行列式,代表了 S 的值:
S=∣∣∣a11a21a12a22∣∣∣
行列式不过就是将矩阵的括号改成了两条竖线,用竖线包着的元素,最终可以算出一个数,这个数就是行列式,行列式就是一个数,这个数是不同行不同列元素乘积的代数和。而矩阵本质为表格或数组,这是两者不同之处。
如果继续推,可以推出:在二维空间,行列式是面积;在三维空间,行列式是体积;在高维空间,行列式是一个数。换句话说,就是由n个向量组成的线性无关向量组,可以表示成行列式,并且算出的结果肯定不为0。以次可推,由n个向量组成的线性相关向量组表示成的行列式值为0。
(四)特征值与特征向量
特征值与特征向量在线性代数中是最难理解的内容,尤其在阅读国内教程时,直接一个定义拍到脸上,让人措手不及。特征值与特征向量是线性代数的核心,在机器学习算法中应用十分广泛。1、定义
首先,讲到特征值与特征向量,必先讲到定义:设 A 是 n 阶矩阵,如果存在一个数 λ 及非零的 n 维列向量 α ,使得
Aα=λα
成立,则称 λ 是矩阵 A 的一个特征值,称非零向量 α 是矩阵 A 属于特征值 λ 的一个特征向量。
观察这个定义可以发现,特征值是一个数,特征向量是一个列向量,一个矩阵乘以一个向量就等于一个数乘以一个向量。这个定义感觉太抽象了,我们来举一个具体的例子:
设 A 是 3 阶矩阵,
A=⎡⎣⎢11−31−21−123⎤⎦⎥
存在一个数 λ ,
λ=4
且存在一个非零的 3 维列向量 α ,
α=⎡⎣⎢−4517⎤⎦⎥
使得 Aα = λα,即
⎡⎣⎢11−31−21−123⎤⎦⎥⎡⎣⎢−4517⎤⎦⎥=4⎡⎣⎢−4517⎤⎦⎥(4)
则称 λ=4 为矩阵A的特征值,
(为了方便,简称 4 为特征值)
也称 α=[ -4, 5, 17 ]T 是矩阵A属于特征值为 4 的一个特征向量。
(为了方便,简称 [ -4, 5, 17 ]T 为特征向量)
对于上面的(4)式,我们可以把它还原为方程组验证此式是否成立,还原过程如下:
⎡⎣⎢⎢11−31−21−123⎤⎦⎥⎥⎡⎣⎢(−4)(5)(17)⎤⎦⎥=4⎡⎣⎢−4517⎤⎦⎥
⟹−4⎡⎣⎢11−3⎤⎦⎥+5⎡⎣⎢1−21⎤⎦⎥+17⎡⎣⎢−123⎤⎦⎥=4⎡⎣⎢−4517⎤⎦⎥
⟹⎧⎩⎨1×(−4)1×(−4)(−3)×(−4)+++1×5(−2)×51×5+++(−1)×172×173×17===4×(−4)4×54×17
⟹⎧⎩⎨−4−412+−+5105−++173451===−162068
显然,每个等式两边相等, Aα = λα 成立!(如果不知道为什么可以还原成方程组的话,请翻回到上面的非齐次方程组部分,可发现在这里 α 相当于解向量, λα 相当于 b 向量)
2、特征值与特征向量的个数
如果是自学线性代数的话,很容易有这么一个误区:认为一个矩阵的特征值与特征向量只有一个。其实,一个矩阵的特征值可以有多个,相应地,特征向量的个数也随着特征值的数量的变化而变化。总的来说,一个n行n列的矩阵的特征值个数少于或等于 n 个。
还是以矩阵A为例,满足 Aα = λα 的式子有:
(1)
⎡⎣⎢11−31−21−123⎤⎦⎥⎡⎣⎢−4517⎤⎦⎥=4⎡⎣⎢−4517⎤⎦⎥
特征值 λ1 = 4,特征向量 α1 = [ -4 5 17 ]T。
(2)
⎡⎣⎢11−31−21−123⎤⎦⎥⎡⎣⎢111⎤⎦⎥=1⎡⎣⎢111⎤⎦⎥
特征值 λ2 = 1,特征向量 α2 = [ 1 1 1 ]T。
(3)
⎡⎣⎢11−31−21−123⎤⎦⎥⎡⎣⎢1−31⎤⎦⎥=−3⎡⎣⎢1−31⎤⎦⎥
特征值 λ3 = -3,特征向量 α3 = [ 1 -3 1 ]T。
另外,一个特征值对应的特征向量的个数也不一定只有一个。 (由于这句话会引申出特别多的性质,所以本文就不举这句话的例子了)
3、给定一个矩阵,求特征值与特征向量的方式
求特征值与特征向量为这么一个过程:设A为n阶矩阵,a为非零列向量,λ是一个数,Aa=λα,α≠0
移项,
⟹λα−Aα=0
利用结合律,由于 λ 是一个数不能直接减矩阵A,所以给 λ 乘以一个单位矩阵E。假设E为2阶单位矩阵,E=(1001),即从左上角到右下角的对角线上的元素全为1,其余为0,
⟹(λE−A)α=0(5)
把(5)式中的矩阵(λE-A)看做是矩阵B,把a列向量看做是x解向量,那么Ax=0是一个齐次线性方程组,由于列向量x不等于0,所以这个齐次线性方程组没有零解,矩阵A每行当作列向量组成的向量组线性相关,于是根据上面行列式的结论,矩阵A写成行列式|A|后算出的结果为0,
⟹|λE−A|=0(6)
解(6)式即可解出多个 λ 值,如 λ1, λ2, λ3 … λn ,将 λi 值代回到(5)式,按照求解齐次线性方程组的方式,即可解出属于 λi 的非零特征向量 ai 。
⟹(λiE−A)a=0⟹αi=[a1,a2,...,an]T
由于本文对行列式介绍的篇幅太少,而求特征值与特征向量会涉及对行列式的计算,所以博主我就不举例子了(其实是懒)。
4、特征值与特征向量该怎么理解
仔细看本文的童鞋就会发现,一个矩阵并非只是单纯的一张表格、数组,它还代表了某种神奇的魔力,与某个向量相乘后,还能变成一个数。换句话说,保存着很多个数的矩阵经过与特定的向量相乘后,塌缩成了一个数。Aa=λα
对于特征值与特征向量,有许多不同的理解,我自己从网络上的观点总结了一下,大概分为三种理解:
第一种理解:从向量的角度来看,一个列向量在左乘一个矩阵后,会经过一系列的线性变换,最终向量的长度会变成原来的 λ 倍。
第二种理解:从矩阵的角度来看,矩阵是一种线性变化的描述,特征向量是一个不变的方向,特征值是线性变化的结果。
第三种理解:从向量空间的角度来看,因为不同特征值对应的特征向量线性无关,把每个特征向量看做是一个坐标轴,特征值是对应坐标轴(即特征向量)的坐标值。简单来说,就是用特征值(坐标)与特征向量(坐标轴)来表示原矩阵。
以上三种理解由浅入深,第三种理解才是本质的理解,但首先需要对向量空间有深刻的理解。
二、一些不错的学习资源
本文讲述的线性代数仅为入门知识,乃整个线代学科的冰山一角,虽然文章中多处吐槽了国内的线性代数教材,但是学习线代还是离不开教材的,推荐老美的《线性代数及其应用》。其实网上也有不少好的线性代数资料,以下列举部分我看过的、或参考的资料。(一)视频
如果不是为了考试的话,推荐直接看视频学习。1、《麻省理工公开课:线性代数》
2、《可汗学院公开课:线性代数》
(二)博文
列举一些写得比较好的博文:1、线代的入门:《如何生动有趣的入门线性代数》
2、线代的基础:《线性代数知识汇总》
3、线代的理解:《关于线性代数》
4、结合概率统计的线性回归算法:《机器学习之线性回归及代码示例》
5、主成分分析法(PCA)的原理:《一分钟理解 PCA 的原理》
6、PCA的简单解释:《浅解PCA》
7、PCA的通俗理解:《通俗理解PCA降维作用》
8、人脸识别之特征脸算法理论:《特征脸EigenFace与PCA》
9、特征脸的实战:《运用特征脸方法的基于Opencv的猫脸检测实现》
10、矩阵的md格式参考于:《使用LaTeX写矩阵》
最后一点点话
以上内容的整理花了我不少时间,有误之处,请多多指点。转载请留言,原创于:http://blog.csdn.net/a727911438?viewmode=contents
相关文章推荐
- Matlab与线性代数 -- 矩阵的特征值与特征向量
- [线性代数]矩阵的特征值与特征向量
- 利用python做矩阵的简单运算(行列式、特征值、特征向量等的求解)
- 协方差矩阵相关概念、性质、应用意义及矩阵特征向量的用处
- 矩阵的特征值与特征向量以及相似矩阵
- C语言调用MKL进行矩阵计算—特征值特征向量求解
- matlab求矩阵前k小的特征值和对应的特征向量
- 【线性代数】在空间中的向量、矩阵与行列式
- 矩阵的特征值、特征向量
- 矩阵复习四-特征值与特征向量
- 矩阵及其变换、特征值与特征向量的物理意义
- 关于矩阵的特征向量和特征值的含义
- 总结r(A)=1的矩阵特征向量与特征值
- 线性代数矩阵论——特征值特征向量相似矩阵应用示例
- mkl中dgeev求解矩阵的特征向量和特征值
- 对矩阵、特征值、特征向量的一些认识
- 矩阵及其变换、特征值与特征向量的物理意义
- 矩阵的特征向量与特征值的几何意义
- 矩阵及其变换、特征值与特征向量的物理意义
- 【Python】【矩阵】协方差矩阵;特征值;特征向量
