山东省第八届acm省赛 Return of the Nim

Problem Description

Sherlock and Watson are playing the following modified version of Nim game:
There are n piles of stones denoted as 

,

,...,

,
and n is a prime number;
Sherlock always plays first, and Watson and he move in alternating turns. During each turn, the current player must perform either of the following two kinds of moves:
Choose one pile and remove k(k >0) stones from it;
Remove k stones from all piles, where 1≤k≤the size of the smallest pile.
This move becomes unavailable if any pile is empty.

Each player moves optimally, meaning they will not make a move that causes them to lose if there are still any better or winning moves.

Giving the initial situation of each game, you are required to figure out who will be the winner

Input

The first contains an integer, g, denoting the number of games. The 2×g subsequent lines describe
each game over two lines:

1. The first line contains a prime integer, n, denoting the number of piles.

2. The second line contains n space-separated integers describing the respective values of 

,

,...,

.
1≤g≤15
2≤n≤30, where n is a prime.
1≤pilesi≤

 where
0≤i≤n−1

Output

For each game, print the name of the winner on a new line (i.e., either "

Sherlock

" or
"

Watson

")

Example Input

2
3
2 3 2
2
2 1

Example Output

Sherlock
Watson

当初做的时候这道题没细看  审题的时候就出了问题 看出来这道题是博弈 没能看清这个题目的本质就是个尼姆博弈加威佐夫博弈 因为堆数n的范围很大 所以做的时候没有思路 写不出东西 最后也就放弃了 后再百度题解发现这道题只需要按照n=2和n》=3分开来看可以 n=2的时候用威佐夫博弈 n》=3用尼姆博弈

、

威佐夫博弈和尼姆博弈的解析，之前看过转发过博客，直接贴过来了，关键的还是普安段奇异局势的公式：

威佐夫博奕

1、问题模型：有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

2、解决思路：A：设（ai,bi）（ai ≤bi  ,i=0，1，2，…,n)表示两堆物品的数量并称其为局势，如果甲面对（0，0），那么甲已经输了，这种局势我们称为奇异局势。前几个奇异局势是：（0，0）、（1，2）、（3，5）、（4，7）、（6，10）、（8，13）、（9，15）、（11，18）、（12，20）。任给一个局势（a，b），如下公式判断它是不是奇异局势： ak =[k（1+√5）/2]，bk= ak + k  （k=0，1，2，…,n 方括号表示取整函数）。（证明见百度百科）

B：详见 http://www.freopen.com/?p=10512）

3、满足上公式的局势性质：

（1）任何自然数都包含在一个且仅有一个奇异局势中。

     由于ak是未在前面出现过的最小自然数，所以有ak > ak-1 ，而 bk= ak + k > ak-1 + k-1 = bk-1 > ak-1 。所以性质成立。

（2）任意操作都可将奇异局势变为非奇异局势。

    若只改变奇异局势（ak，bk）的某一个分量，那么另一个分量不可能在其他奇异局势中，所以必然是非奇异局势。如果使（ak，bk）的两个分量同时减少，则由于其差不变，且不可能是其他奇异局势的差，因此也是非奇异局势

（3）采用适当的方法，可以将非奇异局势变为奇异局势。

     假设面对的局势是（a,b），若 b = a，则同时从两堆中取走 a 个物体，就变为了奇异局势（0，0）；如果a = ak ，b > bk，那么，取走b  – bk个物体，即变      为奇异局势；如果 a = ak ，  b < bk ,则同时从两堆中拿走 ak – ab – ak个物体,变为奇异局势（ ab – ak , ab – ak+ b – ak）；如果a > ak ，
           b= ak + k,则从第一堆中拿走多余的数量a – ak 即可；如果a < ak ，b= ak + k,分两种情况，第一种，a=aj （j < k）,从第二堆里面拿走 b – bj 即可； 第      二种，a=bj （j < k）,从第二堆里面拿走 b – aj 即可。

尼姆博弈

1、问题模型：有三堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

2、解决思路：用（a，b，c）表示某种局势，显证（0，0，0）是第一种奇异局势，无论谁面对奇异局势，都必然失败。第二种奇异局势是（0，n，n），只要与对手拿走一样多的物品，最后都将导致（0，0，0）。

  搞定这个问题需要把必败态的规律找出：(a,b,c)是必败态等价于a^b^c=0(^表示异或运算）。

  证明:(1)任何p(a,b,c)=0的局面出发的任意局面(a,b,c’);一定有p(a,b,c’)不等于0。否则可以得到c=c’。

      （2）任何p(a,b,c)不等于0的局面都可以走向 p(a,b,c)=0的局面

       (3）对于 (4,9,13) 这个容易验证是奇异局势 


             

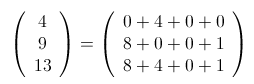
       其中有两个8，两个4，两个1，非零项成对出现，这就是尼姆和为  零的本质。别人要是拿掉13里的8或者1，那你就拿掉对应的9  中的那个8或者1；别人要是拿        掉13里的4，你就拿掉4里的4；  别人如果拿掉13里的3，就把10作分解，然后想办法满 足非零项成对即可。

ac代码：

[cpp] view
plain copy

#include <cstdio>  

#include <cstring>  

#include <iostream>  

#include <algorithm>  

#include <cmath>  

using namespace std;  

int a[1000];  

int main(){  

    int t;  

    scanf("%d",&t);  

    while(t--){  

        int n;  

        scanf("%d",&n);  

        for(int i=0;i<n;i++){  

            scanf("%d",&a[i]);  

        }  

        if(n==2){  

            if(a[0]<a[1]){  

                swap(a[0],a[1]);  

            }  

            if(floor((a[0]-a[1])*((sqrt(5.0)+1.0)/2.0))!=a[1])//威佐夫博弈的核心判断公式

    {  

                printf("Sherlock\n");  

            }  

            else{  

                printf("Watson\n");  

            }  

        }  

        else{  

            int k=a[0];  

            for(int i=1;i<n;i++){
 //所有堆数异或运算后的值

                k^=a[i];  

            }  

            if(k==0){  

                printf("Watson\n");  

            }  

            else{  

                printf("Sherlock\n");  

            }  

        }  

    }  

    return 0;  

}