≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十九):SVM
2016-11-28 10:09
453 查看
支持向量机——最大边距方法
前言:这节课我人在北京,只能回来之后抄一下笔记,然后对着书和wiki理解一下....有什么错误还请大家及时指出。
------------------------------
数据:有标识、有监督D={(xi,yi)∣xi∈Rp,yi∈{−1,1}}ni=1
模型:f(x)=sign(wx+b)
,线性模型
准则:最大边距
先说一下个人理解的SVM的直觉。下图来自wiki。二次元中的SVM就是想找到一条直线(或者对应高维空间下的超平面)来尽可能的分割开两组数据。比如图中H3和H2这两条直线虽然都可以分开这两组数据,但是显然H3离两组数据都远一些——这就是SVM遵循的最大边距准则。

而在实践中,我们把二类分类分别作为正负1,所以两条距离该分割线平行距离1的直线就应景而生。在这两条直线上的点我们称之为支持向量(SV)。
使得yi=1,yi=−1,wx+b>0wx+b<0⇒wx+b=0
为分割超平面。
2) 一个点到超平面wx+b=0
的距离:
d(x|w,b)=⎧⎩⎨wx+b∥w∥−wx+b∥w∥,y=+1,y=−1
⇒=y(wx+b)∥w∥
3) 分割超平面的正则表示
数据集到某个超平面的距离d(D|w,b)=mind(i|w,b)=miniyi(wxi+b)∥w∥
。将y(wx+b)≥1标准化,则yi(wxi+b)∥w∥≥1∥w∥
。
4) 最大边距准则
maxw,bd(D|w,b)
5) 线性可分时的SVM
max1∥w∥
s.t.y(wxi+b)≥1
等同于
min12∥w∥2
s.t.y(wxi+b)≥1
这样就有了一个sign分类器。
6) support vector:分离超平面落在隔离带的边缘,满足yi(wxi+b)=1
的xi
被称为SV。
7) 优点:
对测试误差错识小
稀疏性
自然直观
有效
有理论深度(这话的意思是,又可以造出来一堆论文了么?)
作为松弛变量。
这样原来的最优化问题就变成
min12∥w∥2+C∑iξi
s.t.yi(wi+b)≥1−ξi
最优的分类器则为f∗(x)=w∗x+b∗
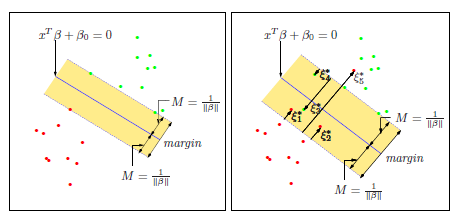
这里大概示意了ξ
的应用场景。左边是上述完全可分的情况,右边是没法分开,所以我们容忍一些误差,只要误差之和在一个可以接受的范围之内。
原来的数据集是:D={(xi,yi)∣xi∈Rp,yi∈{−1,1}}ni=1
然后定义一个从低维到高维的映射:Φ
,使得xΦ→z。其中x原本属于Rp,此时被映射到一个高维的Rq
,可为无限维Hilbert空间(这里我只是照抄笔记...)。
映射之后的D′={(zi,yi)∣zi∈Rq,yi∈{−1,1}}ni=1
,之后就是传统的寻找一个线性平面。
Φ
的例子:
Φ(x)=(Φ1(x),Φ2(x),Φ3(x))=(x21,2x1x2,x22)
,这样就打散到一个高维的空间(圆)。
下节课是线性SVM的计算。
这节课主要是讲线性优化的对偶问题。感觉这东西貌似在运筹学的时候被折腾过一遍,现在又来了-_-||
附赠个老的掉牙的段子...
有人问经济学家一个数学问题,经济学家表示不会解...
然后那个人把这个数学问题转成了一个等价的最优化问题,经济学家立马就解出来了...
好吧,我还是乖乖的赘述一遍对偶问题吧,表示被各种经济学最优化问题折磨过的孩子这点儿真是不在话下。
--------------------------------------------------------------------
一个典型的最优化问题形如:
minf0(x)
s.t.fi(x)≤0, i∈{1,…,m}
(不等式约束)
hi(x)=0, i∈{1,…,p}
(等式约束)
2) 优化问题的Lagrange (拉格朗日)函数
L(x,λ,ν)=f0(x)+∑mi=1λifi(x)+∑pi=1νihi(x).
λi,νi>0,∀i
3) 对偶函数
g(λ,ν)=infx∈DL(x,λ,ν)=infx∈D(f0(x)+∑mi=1λifi(x)+∑pi=1νihi(x))
称为该优化问题的对偶函数。此时,
∇xL(x,λ,ν)=0
,显然这个时候一阶偏导数为0。
4) 对偶问题
我们称maxg(λ,ν),s.t.λ≥0
为原优化问题的对偶问题,可化为最优化问题的标准形式min−g(λ,ν),s.t.−λ≤0
。
如果原优化问题为凸优化,则g(⋅)
必为凹函数,从而最终的标准形式依旧是一个凸优化问题。
5) 弱对偶性
令x∗
为原问题的解,则p∗=f0(x∗),且fi(x∗)≤0,hi(x∗)=0
.
令(λ∗,ν∗)
为对偶问题的解,则d∗=g(λ∗,ν∗);
λ∗≥0
.
定理(弱对偶性):d∗≤p∗
,即对偶问题的优化值必然小于等于原问题优化值。
6) 强对偶性
当d∗=p∗
时,两者具有强对偶性;满足该条件的称之为constraint qualifications,如Sliter定理。
强对偶性满足的时候,原优化问题就可以化为一个二步优化问题了。
7) KTT条件(库恩-塔克条件)
局部最优化成立的必要条件:
∇xL(x,λ,ν)=∇f(x∗)+∑mi=1λi∇fi(x∗)+∑lj=1νj∇hj(x∗)=0
(一阶条件)
λifi(x∗)=0,∀i=1,…,m.
λi≥0,∀i
fi(x∗)≤0,∀i=1,…m
hj(x∗)=0,∀j=1,…,p
注:SVM满足强对偶性,所以可以直接解对偶问题。
上节课可知,SVM的最优化问题为:
min12∥w∥2+C∑iξi
s.t.yi(wi+b)≥1−ξi,∀i
写成标准形式就是
min12∥w∥2+C∑iξi
s.t.1−ξi−yi(wi+b)≤0,∀i
−ξi≤0,∀i
这样这里总计有2N个约束条件。
对应的Lagrange函数为:minw,ξ,b{12∥w∥2+C∑ni=1ξi+∑ni=1λi[1−yi(w′⋅xi−b)−ξi]−∑ni=1μiξi}
这样一阶条件就是
∂L∂wk=wk+∑ni=1λi(−yixki)=0
⇒w=∑ni=1λi(yixi)
∂L∂b=∑ni=1λi(−yi)=0
⇒∑ni=1λiyi=0
∂L∂ξk=C−λk−μk=0
⇒C−λk−μk=0,∀k
这样最后我们有L∗=−12∑iλiyi(w′xi)+∑iλi(1−b)
.
3) 对偶函数
这里的对偶函数就是g(λ,μ)=−12∑i∑j(λiyi)(λjyj)(x′ixj)+∑iλi
4) 对偶问题
min−g(λ,μ)=12∑i∑j(λiyi)(λjyj)(x′ixj)−∑iλi
s.t.∑iλiyi=0
0≤λi≤C
μi≥0
5) KKT条件
w=∑λiyixi
λi(1−yi(w′xi+b)−ξi)=0
∑λiyi=0
0≤λi≤C
λi[yi(w′xi+b)−ξi]=0
μiξi=0
μi≥0
6) SVM分类器
解对偶问题,得到λ∗
,
μ∗
计算w∗=∑iλiyixi
计算b∗:找到一个<0λi<C(非边界上),从而满足{1−yi(w′⋅xi−b)=0ξi=0。由yi=±1,我们可得(w′⋅xi−b)=yi⇒b=yi−w′⋅xi=yi−∑jλjyj(x′jxi)
平面分类器:
y=w∗x+b,
y^=sign(w∗x+b)=sign(∑jλjyj(x′jxi))
,故只与内积有关。
这样下节课就会讲到解对偶问题的方法,以及SVM和kernel methods的联系。
前言:这节课我人在北京,只能回来之后抄一下笔记,然后对着书和wiki理解一下....有什么错误还请大家及时指出。
------------------------------
1. 背景
问题:两类分类问题数据:有标识、有监督D={(xi,yi)∣xi∈Rp,yi∈{−1,1}}ni=1
模型:f(x)=sign(wx+b)
,线性模型
准则:最大边距
先说一下个人理解的SVM的直觉。下图来自wiki。二次元中的SVM就是想找到一条直线(或者对应高维空间下的超平面)来尽可能的分割开两组数据。比如图中H3和H2这两条直线虽然都可以分开这两组数据,但是显然H3离两组数据都远一些——这就是SVM遵循的最大边距准则。

而在实践中,我们把二类分类分别作为正负1,所以两条距离该分割线平行距离1的直线就应景而生。在这两条直线上的点我们称之为支持向量(SV)。
2. 线性可分时的SVM
1) 线性可分:存在w,b使得yi=1,yi=−1,wx+b>0wx+b<0⇒wx+b=0
为分割超平面。
2) 一个点到超平面wx+b=0
的距离:
d(x|w,b)=⎧⎩⎨wx+b∥w∥−wx+b∥w∥,y=+1,y=−1
⇒=y(wx+b)∥w∥
3) 分割超平面的正则表示
数据集到某个超平面的距离d(D|w,b)=mind(i|w,b)=miniyi(wxi+b)∥w∥
。将y(wx+b)≥1标准化,则yi(wxi+b)∥w∥≥1∥w∥
。
4) 最大边距准则
maxw,bd(D|w,b)
5) 线性可分时的SVM
max1∥w∥
s.t.y(wxi+b)≥1
等同于
min12∥w∥2
s.t.y(wxi+b)≥1
这样就有了一个sign分类器。
6) support vector:分离超平面落在隔离带的边缘,满足yi(wxi+b)=1
的xi
被称为SV。
7) 优点:
对测试误差错识小
稀疏性
自然直观
有效
有理论深度(这话的意思是,又可以造出来一堆论文了么?)
3.一般的(线性)SVM
不满足约束的时候,可以做一些放松——引入ξi≥0作为松弛变量。
这样原来的最优化问题就变成
min12∥w∥2+C∑iξi
s.t.yi(wi+b)≥1−ξi
最优的分类器则为f∗(x)=w∗x+b∗

这里大概示意了ξ
的应用场景。左边是上述完全可分的情况,右边是没法分开,所以我们容忍一些误差,只要误差之和在一个可以接受的范围之内。
4.非线性的SVM
这里的直觉大概是,在低维空间较为稠密的点,可以在高维空间下变得稀疏。从而可能可以找到一个高维空间的线性平面,把他们分开。原来的数据集是:D={(xi,yi)∣xi∈Rp,yi∈{−1,1}}ni=1
然后定义一个从低维到高维的映射:Φ
,使得xΦ→z。其中x原本属于Rp,此时被映射到一个高维的Rq
,可为无限维Hilbert空间(这里我只是照抄笔记...)。
映射之后的D′={(zi,yi)∣zi∈Rq,yi∈{−1,1}}ni=1
,之后就是传统的寻找一个线性平面。
Φ
的例子:
Φ(x)=(Φ1(x),Φ2(x),Φ3(x))=(x21,2x1x2,x22)
,这样就打散到一个高维的空间(圆)。
下节课是线性SVM的计算。
这节课主要是讲线性优化的对偶问题。感觉这东西貌似在运筹学的时候被折腾过一遍,现在又来了-_-||
附赠个老的掉牙的段子...
有人问经济学家一个数学问题,经济学家表示不会解...
然后那个人把这个数学问题转成了一个等价的最优化问题,经济学家立马就解出来了...
好吧,我还是乖乖的赘述一遍对偶问题吧,表示被各种经济学最优化问题折磨过的孩子这点儿真是不在话下。
--------------------------------------------------------------------
1. 对偶问题的一般情况
1) 优化问题一个典型的最优化问题形如:
minf0(x)
s.t.fi(x)≤0, i∈{1,…,m}
(不等式约束)
hi(x)=0, i∈{1,…,p}
(等式约束)
2) 优化问题的Lagrange (拉格朗日)函数
L(x,λ,ν)=f0(x)+∑mi=1λifi(x)+∑pi=1νihi(x).
λi,νi>0,∀i
3) 对偶函数
g(λ,ν)=infx∈DL(x,λ,ν)=infx∈D(f0(x)+∑mi=1λifi(x)+∑pi=1νihi(x))
称为该优化问题的对偶函数。此时,
∇xL(x,λ,ν)=0
,显然这个时候一阶偏导数为0。
4) 对偶问题
我们称maxg(λ,ν),s.t.λ≥0
为原优化问题的对偶问题,可化为最优化问题的标准形式min−g(λ,ν),s.t.−λ≤0
。
如果原优化问题为凸优化,则g(⋅)
必为凹函数,从而最终的标准形式依旧是一个凸优化问题。
5) 弱对偶性
令x∗
为原问题的解,则p∗=f0(x∗),且fi(x∗)≤0,hi(x∗)=0
.
令(λ∗,ν∗)
为对偶问题的解,则d∗=g(λ∗,ν∗);
λ∗≥0
.
定理(弱对偶性):d∗≤p∗
,即对偶问题的优化值必然小于等于原问题优化值。
6) 强对偶性
当d∗=p∗
时,两者具有强对偶性;满足该条件的称之为constraint qualifications,如Sliter定理。
强对偶性满足的时候,原优化问题就可以化为一个二步优化问题了。
7) KTT条件(库恩-塔克条件)
局部最优化成立的必要条件:
∇xL(x,λ,ν)=∇f(x∗)+∑mi=1λi∇fi(x∗)+∑lj=1νj∇hj(x∗)=0
(一阶条件)
λifi(x∗)=0,∀i=1,…,m.
λi≥0,∀i
fi(x∗)≤0,∀i=1,…m
hj(x∗)=0,∀j=1,…,p
注:SVM满足强对偶性,所以可以直接解对偶问题。
2. 对偶问题应用于SVM
1) SVM的最优化问题上节课可知,SVM的最优化问题为:
min12∥w∥2+C∑iξi
s.t.yi(wi+b)≥1−ξi,∀i
写成标准形式就是
min12∥w∥2+C∑iξi
s.t.1−ξi−yi(wi+b)≤0,∀i
−ξi≤0,∀i
这样这里总计有2N个约束条件。
对应的Lagrange函数为:minw,ξ,b{12∥w∥2+C∑ni=1ξi+∑ni=1λi[1−yi(w′⋅xi−b)−ξi]−∑ni=1μiξi}
这样一阶条件就是
∂L∂wk=wk+∑ni=1λi(−yixki)=0
⇒w=∑ni=1λi(yixi)
∂L∂b=∑ni=1λi(−yi)=0
⇒∑ni=1λiyi=0
∂L∂ξk=C−λk−μk=0
⇒C−λk−μk=0,∀k
这样最后我们有L∗=−12∑iλiyi(w′xi)+∑iλi(1−b)
.
3) 对偶函数
这里的对偶函数就是g(λ,μ)=−12∑i∑j(λiyi)(λjyj)(x′ixj)+∑iλi
4) 对偶问题
min−g(λ,μ)=12∑i∑j(λiyi)(λjyj)(x′ixj)−∑iλi
s.t.∑iλiyi=0
0≤λi≤C
μi≥0
5) KKT条件
w=∑λiyixi
λi(1−yi(w′xi+b)−ξi)=0
∑λiyi=0
0≤λi≤C
λi[yi(w′xi+b)−ξi]=0
μiξi=0
μi≥0
6) SVM分类器
解对偶问题,得到λ∗
,
μ∗
计算w∗=∑iλiyixi
计算b∗:找到一个<0λi<C(非边界上),从而满足{1−yi(w′⋅xi−b)=0ξi=0。由yi=±1,我们可得(w′⋅xi−b)=yi⇒b=yi−w′⋅xi=yi−∑jλjyj(x′jxi)
平面分类器:
y=w∗x+b,
y^=sign(w∗x+b)=sign(∑jλjyj(x′jxi))
,故只与内积有关。
这样下节课就会讲到解对偶问题的方法,以及SVM和kernel methods的联系。
相关文章推荐
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(四)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(三)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(三)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十五)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(一)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十一)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十八):神经网络
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(二)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(三)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(二)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(一)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(五)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(七)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(四)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(六)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(三)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(二)
- ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(八)
- 统计学习精要(The Elements of Statistical Learning)课堂笔记(二十二):核函数和核方法
