SVM-支持向量机
2016-11-17 07:38
190 查看
注:本文中所有公式和思路来自于邹博先生的《机器学习升级版》,我只是为了加深记忆和理解写的本文。
我相信搞机器学习的同学应该没有人没听过SVM,但是能清清楚楚的把SVM说明白我想还是会有一点点小难度的,今天我也尝试着把这块介绍一下。
SVM可以分为三种:
线性可分支持向量机:硬间隔最大化 hard margin maximitation、硬间隔支持向量机
线性支持向量机:软间隔最大化 soft margin maximitation、软间隔支持向量机
非线性支持向量机:核函数 kernel function
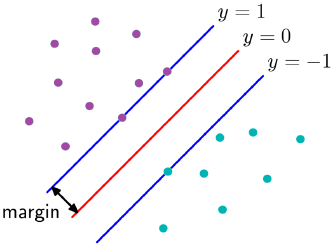
我们都知道SVM其实就是找一个最优分割超平面将两个集合尽可能地分开:
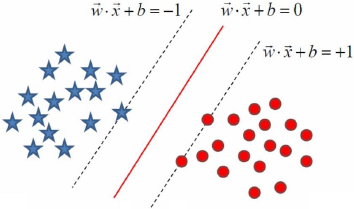
其中落在红色分割面两侧的虚线上的样本我们称之为支撑向量,是这几个向量将超平面支撑起来,如果超平面确定了,我们在虚线以外随意移动其他的样本,不会对超平面产生生任何影响,也就是说这个超平面是由少数的几个向量确定的,所以SVM又被称为稀疏的模型。
从下边这幅图中可以看得出,有n条直线可以将两边的集合完全分开,那么我们怎么找到这个能使两个集合尽量分开的超平面呢?
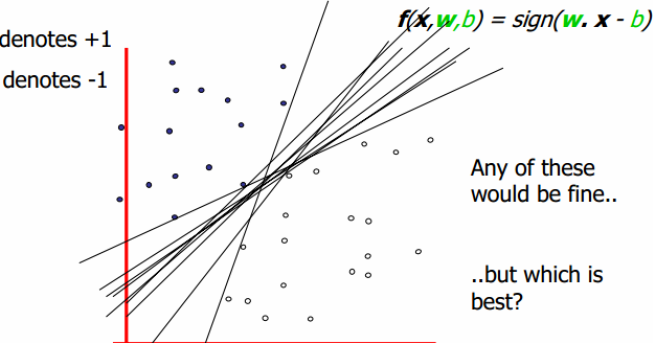
线性可分支持向量机
假设给定一个特征空间上的训练数据集:T = {(x1,y1),(x2,y2) ... (xn,yn)},其中:
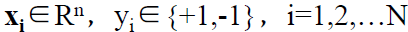
xi为第i个样本实例(如果n>1,x为向量),yi为xi的类标记,当yi = +1时,称xi为正例;当yi = -1时,称xi为负例。
那么现在就来说说怎么找这个间隔最大化,首先看下面这幅图:
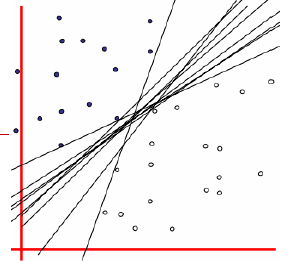
我们看得到图中有n条直线,m个样本点,我们先来取一条直线,假如是n1这条直线,那么我就可以求所有的m个样本点到这条直线的距离,记作n1:diatance11、distance12 ... distnce 1m,我们在这m个点到n1的距离中取一个最小距离,接着我们取第二条线,那么我们就可以求所有的m个样本点到这条直线的距离,记作n2:diatance21、distance22
... distnce 2m,再从中选一个最小的距离,知道所有直线取完,那么我们会得到这么一个数据:
n1:diatance 11、distance 12 ... distnce 1m 取最小的一个距离
n2:diatance 21、distance 22 ... distnce 2m 取最小的一个距离
n3:diatance 31、distance 32 ... distnce 3m 取最小的一个距离
nn:diatance n1、distance n2 ... distnce nm 取最小的一个距离
那么最终会得到n个最小的距离,我们再从这n个最小距离中取一个最大的距离,这不就是最优的么!!!!!!
通过上边的想法,给定线性可分训练数据集,通过间隔最大化得到的分割超平面为:
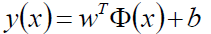
相应的的分类决策函数(输出+-1):
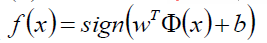
那么我们怎么来进行推导目标函数呢?
根据题设:
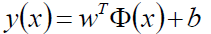
那么就有:
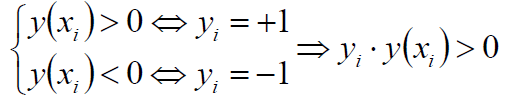
其中y(x)是我们的预测值,如果预测值>0,乘以标记值+1那么就>0;如果预测值为<0,乘以标记值-1那么就>0。
2x+3b+6=0和4x+6b+12=0其实时一条线,我们就通过w和b等比例缩放,改变点到直线的距离,另外除了一个||w||来做归一化,其实如果抛去yi不看的话,那其实不就是距离公式嘛:
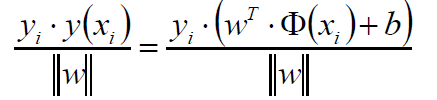
那么我们的目标函数就出来了:
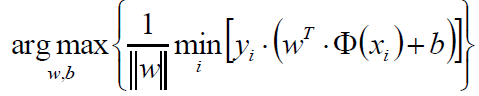
这个式子看起来好像挺复杂,其实仔细一看不就是上边我们推导的最小距离取最大的那个过程嘛。只不过这里把||w||放在了前边而已。
我们知道几何间距和函数间距其实是差了一个归一化:
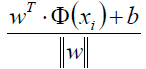
那么加上这么一个||w||有什么好处呢?好处就在于我们总能通过等比例缩放||w||的方法,使得两类点的函数值都满足|y|≥1
既然如此,那么就有了这个一个约束条件,因为我们最初的目的不就是要将所有样本点分开嘛,通过w缩放使得距离至少为1
嘛:
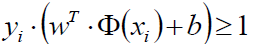
我们再来看原来的目标函数:
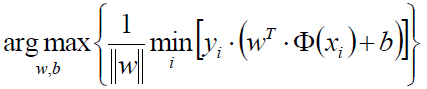
现在可以知道,y*y(x)≥1,那么取最小值不就是1嘛,那后边去的i个1嘛,那就统统的扔掉:
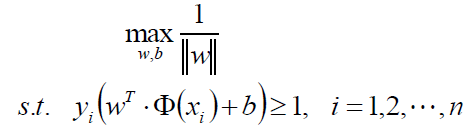
我们可以做如下的等价变换,将求最大变成求最小:
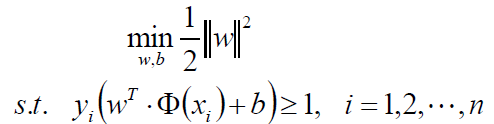
我们现在来看看这目标函数,既然是个二次的,那么就是一个凸的,约束条件也是线性的,那么就是一个凸优化问题,并且是一个满足KKT的,那么我们就可以大胆的使用拉格朗日乘子法:
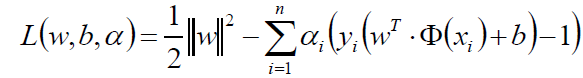
那么我们原函数的问题是一个极小极大问题:
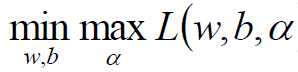
那么原问题的对偶问题就是一个极大极小问题:
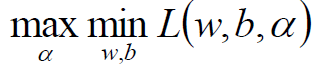
将拉格朗日函数L(w,b,α)分别对w、b求偏导,并令其为0可得:
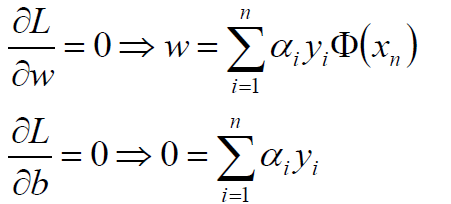
将w、b回代到拉格朗日函数中:
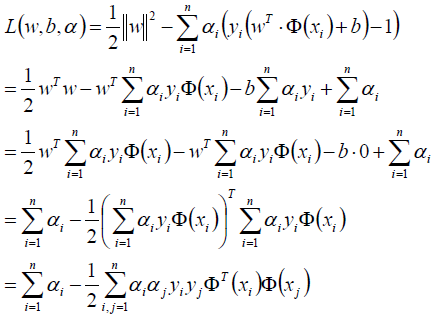
求得α*等于:
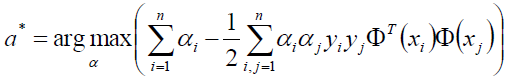
我们似乎还有一个条件没有用上呢:
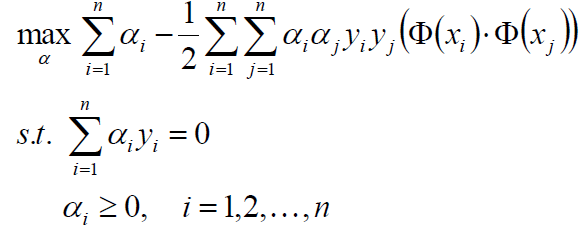
整理目标函数,添加条件:
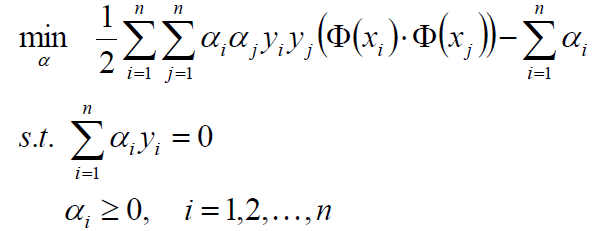
那么现在的问题就剩下了怎么求这个α了,其实有两种办法,一种是SMO,另外一种就是梯度下降。SMO我们将在后文中单独介绍。
线性支持向量机
实际情况中,如果都能像线性可分支持向量机所设想的那样自然是最好的,如果不是呢?
有两个问题:第一,不一定分类完全正确的超平面就是最好的。第二,样本数据本身线性不可分。
若数据线性不可分,则增加松弛因子ξ≥0,使得函数间隔加上松弛因子后大于等于1,这样的话约束条件变为:
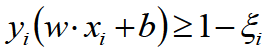
那么线性SVM的目标函数为:
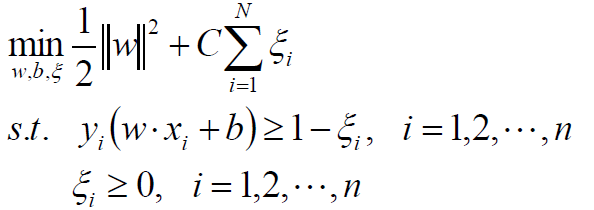
拉格朗日函数:
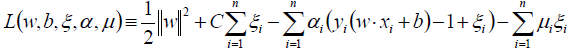
对w、b、ξ求偏导并为0:
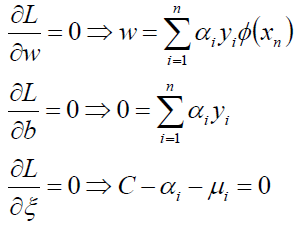
带回到拉格朗日函数:
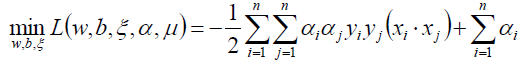
对上式关于α求极大:
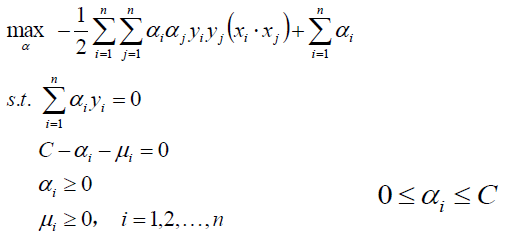
整理得:
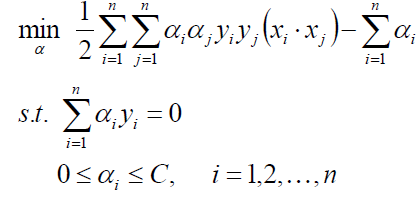
又回到求优化α得问题上,下一篇文章将会介绍SMO得办法求优化α,如果求得了α,带入得到w、b:
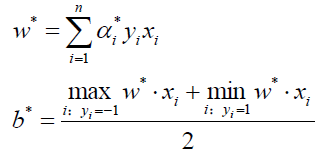
既然w、b都有了,那么分割超平面就有了:
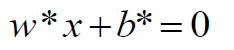
最终套进一个决策函数就完事了。
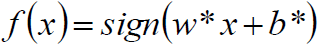
损失函数分析
那么SVM得损失怎么来看呢?
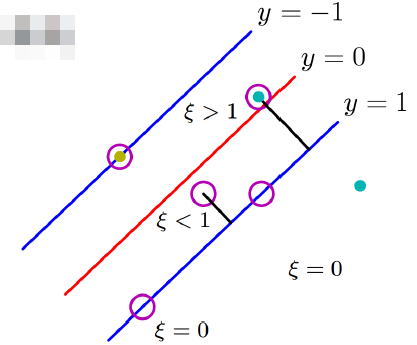
从图中可以清楚地看出,如果样本没有超过y=1或y=-1这两条线之间的话,那么是不惩罚的,如果进入分隔带就要惩罚了,惩罚的力度就是离y得距离,离得越远惩罚越大,也就是说某些点没有超过y=0,虽然分对了,但是任然要惩罚,超过了y=0自然是更要惩罚了,其中ξ就是惩罚力度,分对了并且在分隔带两侧不惩罚,分对了在分隔带以内惩罚0<ξ<1,分错了在分隔带另外一侧的话惩罚大于1。
我们可以从一幅图来形象得说明这个损失:
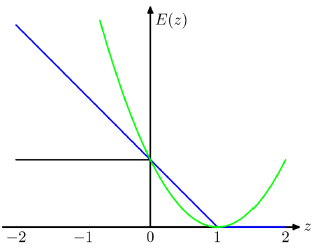
其中蓝色线就是SVM得损失:Hinge loss 或者叫铰链损失、合页损失。
黑色线是误分类率,绿色线是误差平方和。
非线性支持向量机
核函数:我们可以使用核函数,将原始输入空间映射到新的样本空间,从而使原来线性不可分得变成高维得线性可分。
核函数有很多种:
多项式核函数:
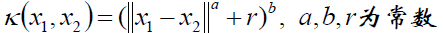
高斯核函数:
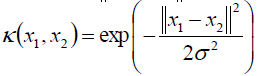
字符串核函数:如果两个字符串满足某条件得字串得余弦相似度。
虽然说有这么多种核函数,其实我就用过一种高斯核函数(RBF)
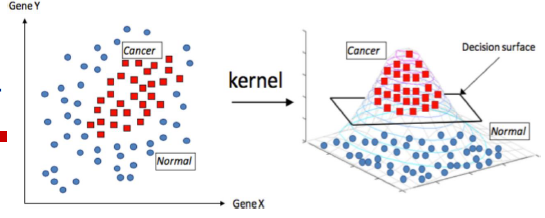
到此SVM就介绍完了,说一下在使用sklearn包的时候几个超参数得作用吧:
C:如果C趋近于无穷大,那么就退化为线性可分得SVM,C越大,分隔带就越窄,泛化能力就越差,C越小,分隔带就越宽,泛化能力越好。
γ:在RBF中,γ是控制每个样本x峰得能力,γ越大,泛化能力就越差,x对应的峰就高瘦,其实就是影响样本的作用范围,γ其实还影响了支持向量的个数,个数多训练速度会慢。
σ:也是影响x得作用范围,如果小的话x得峰就会高瘦,作用范围也小。
以上仅为一家之言,自己的实验总结,具体怎么个情况,还得自己做个实验来尝试。
我相信搞机器学习的同学应该没有人没听过SVM,但是能清清楚楚的把SVM说明白我想还是会有一点点小难度的,今天我也尝试着把这块介绍一下。
SVM可以分为三种:
线性可分支持向量机:硬间隔最大化 hard margin maximitation、硬间隔支持向量机
线性支持向量机:软间隔最大化 soft margin maximitation、软间隔支持向量机
非线性支持向量机:核函数 kernel function
我们都知道SVM其实就是找一个最优分割超平面将两个集合尽可能地分开:

其中落在红色分割面两侧的虚线上的样本我们称之为支撑向量,是这几个向量将超平面支撑起来,如果超平面确定了,我们在虚线以外随意移动其他的样本,不会对超平面产生生任何影响,也就是说这个超平面是由少数的几个向量确定的,所以SVM又被称为稀疏的模型。
从下边这幅图中可以看得出,有n条直线可以将两边的集合完全分开,那么我们怎么找到这个能使两个集合尽量分开的超平面呢?

线性可分支持向量机
假设给定一个特征空间上的训练数据集:T = {(x1,y1),(x2,y2) ... (xn,yn)},其中:
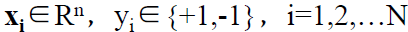
xi为第i个样本实例(如果n>1,x为向量),yi为xi的类标记,当yi = +1时,称xi为正例;当yi = -1时,称xi为负例。
那么现在就来说说怎么找这个间隔最大化,首先看下面这幅图:

我们看得到图中有n条直线,m个样本点,我们先来取一条直线,假如是n1这条直线,那么我就可以求所有的m个样本点到这条直线的距离,记作n1:diatance11、distance12 ... distnce 1m,我们在这m个点到n1的距离中取一个最小距离,接着我们取第二条线,那么我们就可以求所有的m个样本点到这条直线的距离,记作n2:diatance21、distance22
... distnce 2m,再从中选一个最小的距离,知道所有直线取完,那么我们会得到这么一个数据:
n1:diatance 11、distance 12 ... distnce 1m 取最小的一个距离
n2:diatance 21、distance 22 ... distnce 2m 取最小的一个距离
n3:diatance 31、distance 32 ... distnce 3m 取最小的一个距离
nn:diatance n1、distance n2 ... distnce nm 取最小的一个距离
那么最终会得到n个最小的距离,我们再从这n个最小距离中取一个最大的距离,这不就是最优的么!!!!!!
通过上边的想法,给定线性可分训练数据集,通过间隔最大化得到的分割超平面为:
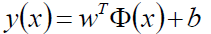
相应的的分类决策函数(输出+-1):
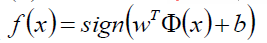
那么我们怎么来进行推导目标函数呢?
根据题设:
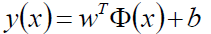
那么就有:
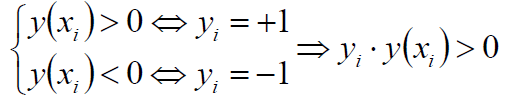
其中y(x)是我们的预测值,如果预测值>0,乘以标记值+1那么就>0;如果预测值为<0,乘以标记值-1那么就>0。
2x+3b+6=0和4x+6b+12=0其实时一条线,我们就通过w和b等比例缩放,改变点到直线的距离,另外除了一个||w||来做归一化,其实如果抛去yi不看的话,那其实不就是距离公式嘛:
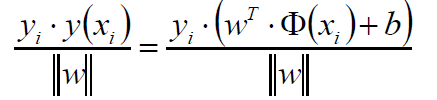
那么我们的目标函数就出来了:
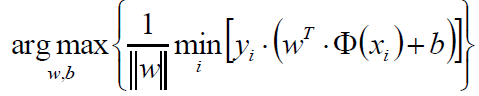
这个式子看起来好像挺复杂,其实仔细一看不就是上边我们推导的最小距离取最大的那个过程嘛。只不过这里把||w||放在了前边而已。
我们知道几何间距和函数间距其实是差了一个归一化:
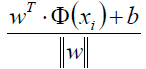
那么加上这么一个||w||有什么好处呢?好处就在于我们总能通过等比例缩放||w||的方法,使得两类点的函数值都满足|y|≥1

既然如此,那么就有了这个一个约束条件,因为我们最初的目的不就是要将所有样本点分开嘛,通过w缩放使得距离至少为1
嘛:
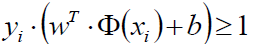
我们再来看原来的目标函数:
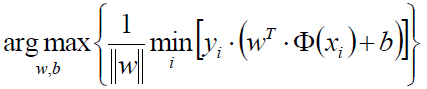
现在可以知道,y*y(x)≥1,那么取最小值不就是1嘛,那后边去的i个1嘛,那就统统的扔掉:
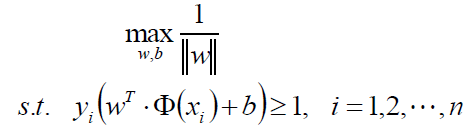
我们可以做如下的等价变换,将求最大变成求最小:
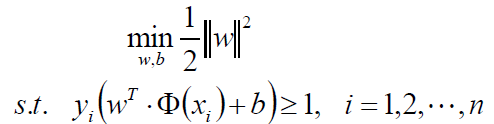
我们现在来看看这目标函数,既然是个二次的,那么就是一个凸的,约束条件也是线性的,那么就是一个凸优化问题,并且是一个满足KKT的,那么我们就可以大胆的使用拉格朗日乘子法:
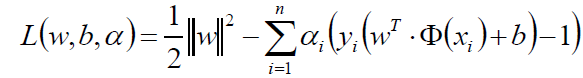
那么我们原函数的问题是一个极小极大问题:
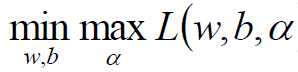
那么原问题的对偶问题就是一个极大极小问题:
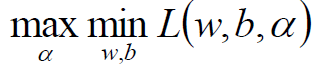
将拉格朗日函数L(w,b,α)分别对w、b求偏导,并令其为0可得:
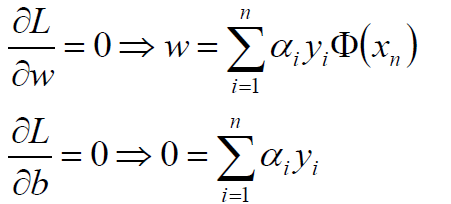
将w、b回代到拉格朗日函数中:
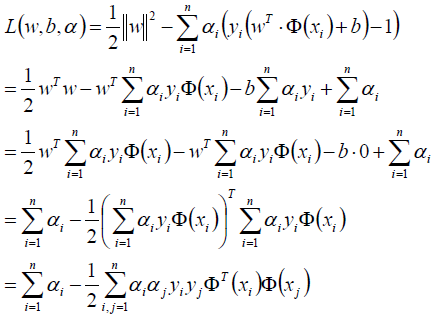
求得α*等于:
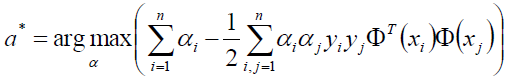
我们似乎还有一个条件没有用上呢:
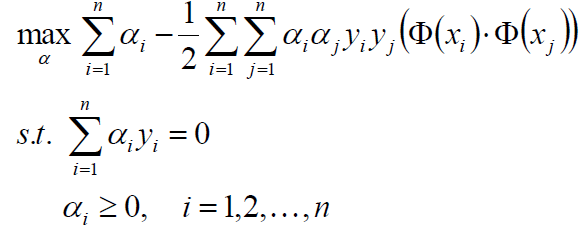
整理目标函数,添加条件:
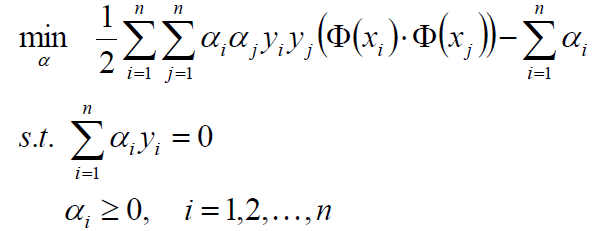
那么现在的问题就剩下了怎么求这个α了,其实有两种办法,一种是SMO,另外一种就是梯度下降。SMO我们将在后文中单独介绍。
线性支持向量机
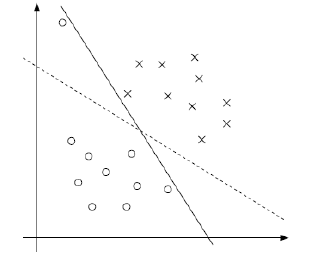
实际情况中,如果都能像线性可分支持向量机所设想的那样自然是最好的,如果不是呢?

有两个问题:第一,不一定分类完全正确的超平面就是最好的。第二,样本数据本身线性不可分。
若数据线性不可分,则增加松弛因子ξ≥0,使得函数间隔加上松弛因子后大于等于1,这样的话约束条件变为:
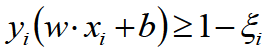
那么线性SVM的目标函数为:
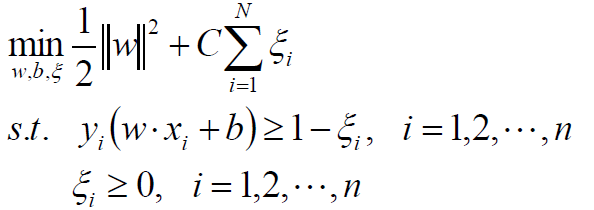
拉格朗日函数:
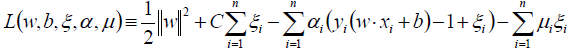
对w、b、ξ求偏导并为0:
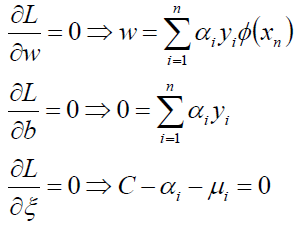
带回到拉格朗日函数:
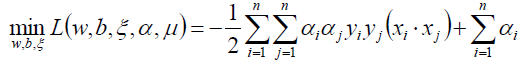
对上式关于α求极大:
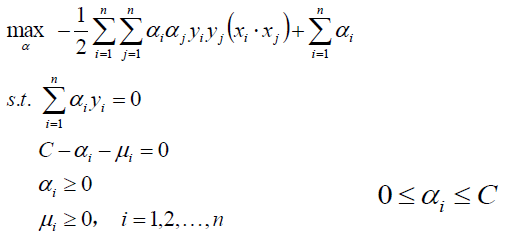
整理得:
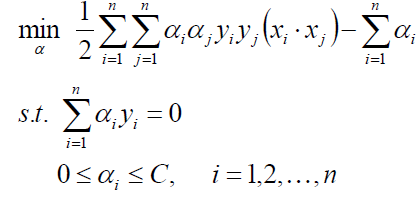
又回到求优化α得问题上,下一篇文章将会介绍SMO得办法求优化α,如果求得了α,带入得到w、b:
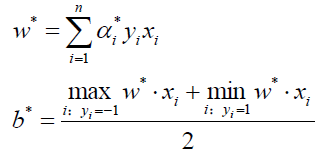
既然w、b都有了,那么分割超平面就有了:
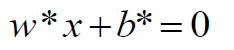
最终套进一个决策函数就完事了。
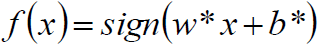
损失函数分析
那么SVM得损失怎么来看呢?

从图中可以清楚地看出,如果样本没有超过y=1或y=-1这两条线之间的话,那么是不惩罚的,如果进入分隔带就要惩罚了,惩罚的力度就是离y得距离,离得越远惩罚越大,也就是说某些点没有超过y=0,虽然分对了,但是任然要惩罚,超过了y=0自然是更要惩罚了,其中ξ就是惩罚力度,分对了并且在分隔带两侧不惩罚,分对了在分隔带以内惩罚0<ξ<1,分错了在分隔带另外一侧的话惩罚大于1。
我们可以从一幅图来形象得说明这个损失:

其中蓝色线就是SVM得损失:Hinge loss 或者叫铰链损失、合页损失。
黑色线是误分类率,绿色线是误差平方和。
非线性支持向量机
核函数:我们可以使用核函数,将原始输入空间映射到新的样本空间,从而使原来线性不可分得变成高维得线性可分。
核函数有很多种:
多项式核函数:
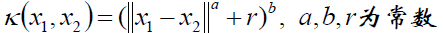
高斯核函数:
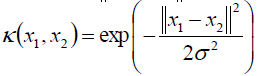
字符串核函数:如果两个字符串满足某条件得字串得余弦相似度。
虽然说有这么多种核函数,其实我就用过一种高斯核函数(RBF)

到此SVM就介绍完了,说一下在使用sklearn包的时候几个超参数得作用吧:
C:如果C趋近于无穷大,那么就退化为线性可分得SVM,C越大,分隔带就越窄,泛化能力就越差,C越小,分隔带就越宽,泛化能力越好。
γ:在RBF中,γ是控制每个样本x峰得能力,γ越大,泛化能力就越差,x对应的峰就高瘦,其实就是影响样本的作用范围,γ其实还影响了支持向量的个数,个数多训练速度会慢。
σ:也是影响x得作用范围,如果小的话x得峰就会高瘦,作用范围也小。
以上仅为一家之言,自己的实验总结,具体怎么个情况,还得自己做个实验来尝试。
相关文章推荐
- 支持向量机SVM和支持向量回归SVR简介——原理方法
- 支持向量SVM分类器的学习记录
- 找到SVM分类器的支持向量(scikit-learn)
- 機器學習中的算法(2)-支持向量機(SVM)基礎
- 機器學習中的算法(2)-支持向量機(SVM)基礎
- 支持向量机(SVM)、支持向量回归(SVR)
- LSSVM(Least Squares SVM)与SVR(支持向量回归)
- 机器学习概念总结笔记(二)——逻辑回归、贝叶斯分类、支持向量分类SVM、分类决策树ID3、
- SVM 中查看支持向量的权重。
- 支持向量机(SVM)、支持向量回归(SVR)
- SVM(Support Vector Machine)读书笔记二(支持向量和Kernel方法)
- [SVM系列之三]间隔与支持向量
- 学习SVM(四) 理解SVM中的支持向量(Support Vector)
- 支持向量机(SVM)、支持向量回归(SVR)
- 支持向量SVM整理
- SVM支持向量分类器原理及OpenCV实现
- 林轩田--机器学习技法--SVM笔记6--支持向量回归(Support+Vector+Regression)
- 支持向量机(SVM)、支持向量回归(SVR)
- 支持向量机(SVM)、支持向量回归(SVR)
- 支持向量机(SVM)、支持向量回归(SVR)
