奇异分解（SVD）

奇异分解

    假设C是m×n矩阵，U是m×m矩阵，其中U的列为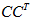

的正交特征向量，V为n×n矩阵，其中V的列为

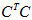
的正交特征向量，再假设r为C矩阵的秩，则存在奇异值分解：

    

    

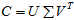
    其中

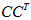
和

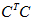
的特征值相同，为

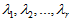
，且

。

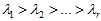
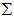
是m

×n的矩阵，

，

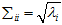
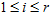
。令

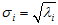
，则

。

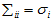
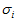
称为矩阵C的奇异值。

    

    

    

    

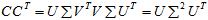
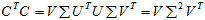
    所以有了矩阵C，可以求得

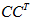
或者

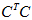
，从求得方阵

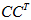
或者

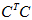
的特征值，利用这些特征值得到

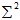
，从而求得

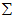
，求得

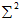
的时候已经求得U或者V。

例题：


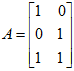
，求A的奇异值分解。

解：


，

，


，

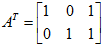
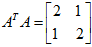
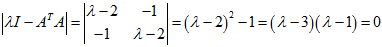
故

，


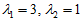
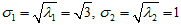
当

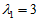
时，特征向量为

，

，

，

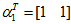
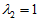
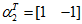
标准化后

，

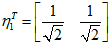
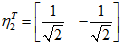
，令


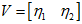
同理，先求

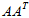
，再求U。


，

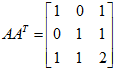
当

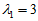
时，特征向量

，

，

，

，



，

，


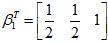
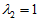
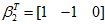
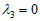
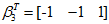
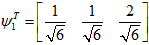
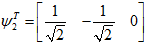
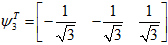
由此可知，

，

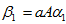
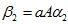
，a是一个常数，然后单位化

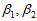
便得到

。

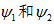
所以


，




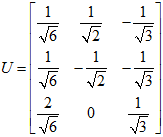
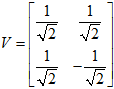
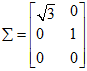
最后得



---------------------------------------------------------------------------------

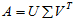
特征值分解——EVD

    在这里，选择一种特殊的矩阵——对称阵（酉空间中叫hermite矩阵即厄米阵）。对称阵有一个很优美的性质：它总能相似对角化，对称阵不同特征值对应的特征向量两两正交。一个矩阵能相似对角化即说明其特
4000
征子空间即为其列空间，若不能对角化则其特征子空间为列空间的子空间。现在假设存在

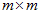
的满秩对称矩阵A，它有m个不同的特征值，设特征值为

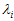
,对应的特征向量为

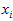
，则有：





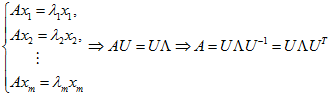
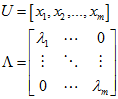
U为的列是两两正交向量，所以它的逆矩阵等于转置矩阵。

奇异值分解——SVD

    假设存在一个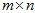

矩阵A，A矩阵将n维空间中的向量映射到k

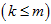
为空间中，

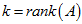
。目标：在n维空间中找一组正交基，使得经过A变换后还是正交的。

    假设这组标准正交基为：

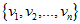
，则A矩阵将这组基映射为

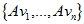
，如果要使他们两两正交，即有以下关系



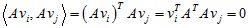
根据假设，也有以下关系：


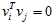
所以如果选择v为

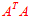
的特征向量的话，由于

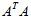
是对称阵，v之间两两正交，那么



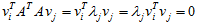
这样就找到了正交基使其映射后还是正交基了，现在，将映射后的正交基单位化：



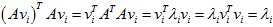
所以


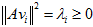
单位化：


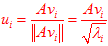
由此得到关系：


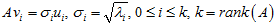
从而得到




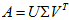
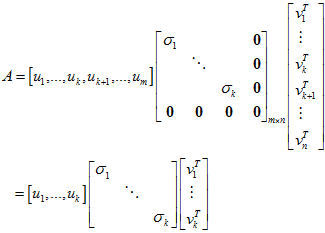
令

，


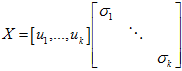
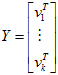
则

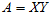
是A的满秩分解。

 
Reference

http://blog.csdn.net/zhongkejingwang/article/details/43053513