Maple计算积分胜出Mathematica一局(案例)
2016-08-30 18:26
561 查看
——虽然Maple的界面用起来比较不称心,我从来不敢否认它的强大。这不,碰上一个简单定积分计算的例子:Maple可以计算出来,mathematica不支持。
∫10x⌊1x⌋dx=?
变换 和 转化 有不同的类型,取决于思路、经验、视野。
我想到的是,原始问题中的定积分,实际就是求面积。
被积函数绘制出来时分段的如下形式;绘出积分对应的面积到蓝色部分:
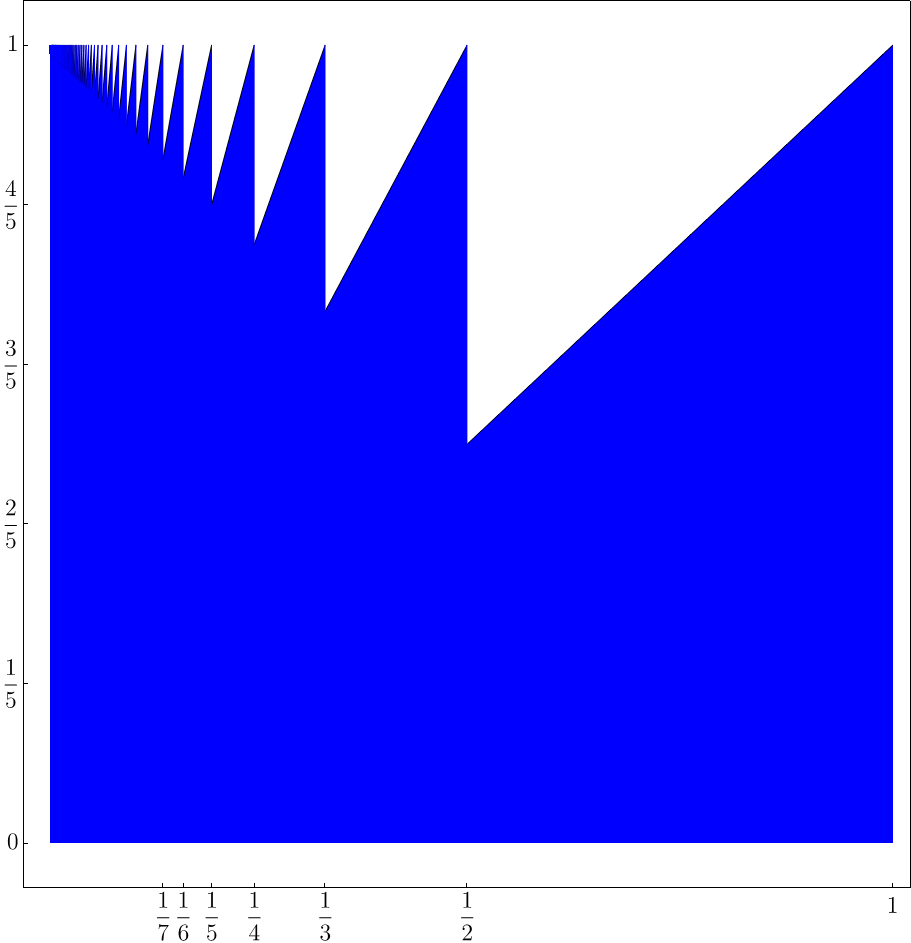
边长为1的正方形面积减去一系列小直角三角形的面积之和即可。这些小三角形的上直角边长度实际对应于下面的值:
{1−12,12−13,13−14,⋯,1k−1k+1,⋯}
侧直角边长为1减去下角点纵坐标。所有的下角点都在直线 y=1−x上。从而容易得到蓝色部分的总面积,也就是定积分的数值:
SBLUE=1−∑k=1+∞12k(k+1)2=π212
这个级数很奇妙。利用这个结果:∑k=1+∞1k2=π26,可以得到:
∑k=1+∞1k(k+1)2=∑k=1+∞((1k−1k+1)−1(k+1)2)
=∑k=1+∞(1k−1k+1)−∑k=1+∞1(k+1)2=1−(π26−1)=2−π26
最终结果从而可以知道。
把图从新画一下,
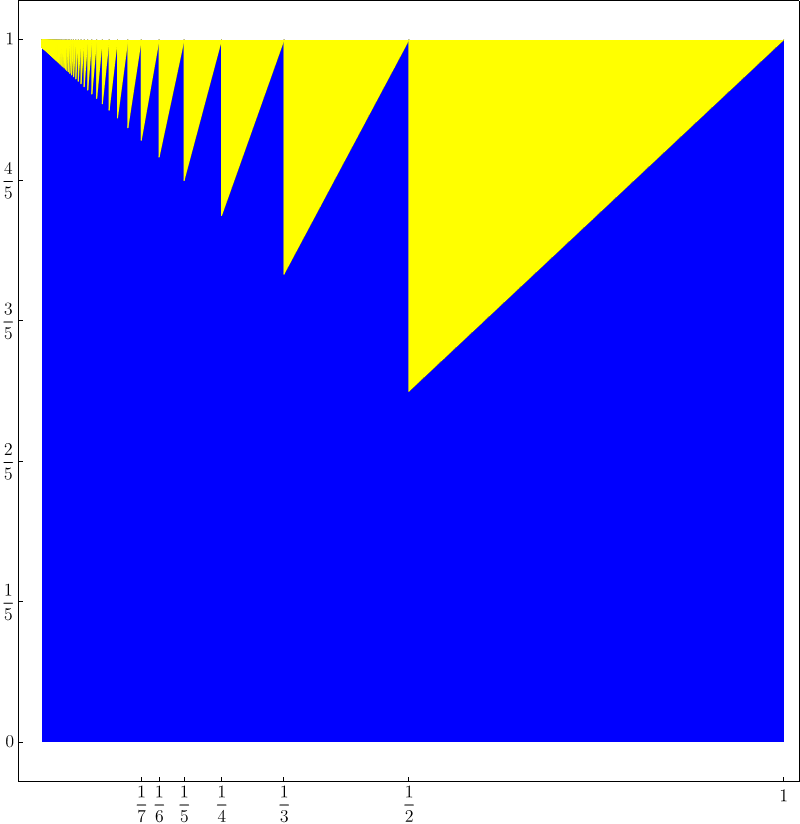
这种图只能象征性表示下。从说明的角度看,似乎不是特别严谨。或者,要交代面积跟积分之间等价,太费口舌。——一直觉得这样的证明,有那么点欠缺,即无法充分、完全地“形式化”为机器能懂的方式。这难道就是人工智能跟人类智能之间根本的差距所在?
此外,看到一个变量代换 t=1x,然后把积分变化为无穷多个(k,k+1) 上积分的级数和的方法,把向下取整函数等价变换为积分区间的下限,更加简单巧妙。——Mathematica做不出这个积分实在让人扼腕叹息啊。
这篇博客真正的重点不在这个积分的求解,而在于,这种坐标轴和轴上标记的绘制小技巧(因为求积分有更简单的变量代换方法);用演示定积分计算的这种方法对应的分析过程,来演示这种绘制坐标轴刻度的技巧,看上去很恰当。
问题
一个包含 向下取整 函数的定积分:∫10x⌊1x⌋dx=?
解答
一些研究
分段函数piecewise求导数、积分原函数都不能用光滑连续函数类似的办法。通常解决较难问题的一般方法是 把待求解的陌生或难的问题,通过一些变换,转化成已经求解过的问题的形式、或者相对熟悉的容易解决的问题的形式变换 和 转化 有不同的类型,取决于思路、经验、视野。
我想到的是,原始问题中的定积分,实际就是求面积。
被积函数绘制出来时分段的如下形式;绘出积分对应的面积到蓝色部分:
<<MaTeX`
Plot[x Floor@(1/x)//Evaluate,
{x,0.01,1},
PlotStyle->Directive[Black,Thin],
Filling->Axis,FillingStyle->Blue,
AxesOrigin->{0,0}, AspectRatio->1,ImageSize->800,WorkingPrecision->30,
PlotPoints->10000,
FrameStyle->BlackFrame,Frame->True,
FrameTicks->{ {Table[{x,MaTeX[x,"DisplayStyle"->True,Magnification->3/2]},{x, Range[0,5]/5}],None},
{Table[{x,MaTeX[x,"DisplayStyle"->True,Magnification->3/2]},{x, 1/Range[1,7]}],None}}
]
边长为1的正方形面积减去一系列小直角三角形的面积之和即可。这些小三角形的上直角边长度实际对应于下面的值:
{1−12,12−13,13−14,⋯,1k−1k+1,⋯}
侧直角边长为1减去下角点纵坐标。所有的下角点都在直线 y=1−x上。从而容易得到蓝色部分的总面积,也就是定积分的数值:
SBLUE=1−∑k=1+∞12k(k+1)2=π212
这个级数很奇妙。利用这个结果:∑k=1+∞1k2=π26,可以得到:
∑k=1+∞1k(k+1)2=∑k=1+∞((1k−1k+1)−1(k+1)2)
=∑k=1+∞(1k−1k+1)−∑k=1+∞1(k+1)2=1−(π26−1)=2−π26
最终结果从而可以知道。
把图从新画一下,
Plot[{1, x Floor@(1/x) // Evaluate}, {x, 0.1^5, 1},
PlotStyle -> {Red, Directive[None, Thin]},
Filling -> {1 -> {{2}, {Red}}}, AxesOrigin -> {0, 0},
AspectRatio -> 1, ImageSize -> 800, WorkingPrecision -> 30,
PlotPoints -> 10000, FrameStyle -> BlackFrame, Frame -> True,
FrameTicks -> {{Table[{x,
MaTeX[x, "DisplayStyle" -> True, Magnification -> 3/2]}, {x,
Range[0, 5]/5}],
None}, {Table[{x,
MaTeX[x, "DisplayStyle" -> True, Magnification -> 3/2]}, {x,
1/Range[1, 7]}], None}}]
这种图只能象征性表示下。从说明的角度看,似乎不是特别严谨。或者,要交代面积跟积分之间等价,太费口舌。——一直觉得这样的证明,有那么点欠缺,即无法充分、完全地“形式化”为机器能懂的方式。这难道就是人工智能跟人类智能之间根本的差距所在?
此外,看到一个变量代换 t=1x,然后把积分变化为无穷多个(k,k+1) 上积分的级数和的方法,把向下取整函数等价变换为积分区间的下限,更加简单巧妙。——Mathematica做不出这个积分实在让人扼腕叹息啊。
这篇博客真正的重点不在这个积分的求解,而在于,这种坐标轴和轴上标记的绘制小技巧(因为求积分有更简单的变量代换方法);用演示定积分计算的这种方法对应的分析过程,来演示这种绘制坐标轴刻度的技巧,看上去很恰当。
相关文章推荐
- 一个Mathematica能解Maple不行的特殊积分
- 利用Maple计算积分操作方法
- Maple计算积分的基本操作讲解
- 积分图计算方法
- 二、利用积分图像法快速计算Haar特征
- Maple OpenMaple (API) 开发系列-3.0 案例
- csdn的博客积分如何计算
- 云计算实施经验集锦 案例经验汇总
- 分布式计算,大型网站技术架构:核心原理与案例分析
- 对三大数学软件 Mathematica 、Maple 、MATLAB 的小测试比较
- 基于案例贯通Spark Streaming流计算框架的运行源码
- Python3 初学实践案例(11)判断质数以及计算一个数字的质因数
- 打印购物小票和计算积分
- 积分图(用于计算块像素差异的快速方法)
- CSDN博客积分计算规则
- 利用积分图像法快速计算Haar特征
- Mathematica 和 MATLAB、Maple 并称为三大数学软件
- 校验和计算案例
- 数学计算软件(Matlab、Mathematica)网页版
- 以物流案例看基于表格存储实时数据流的serverless计算
