PGM - Week 1

Introduction and Overview

Overview and Motivation

Representation

Directed and undirected

Temporal and plate models

Inference

Exact and approximate

Decision making

Learning

Parameters and structure

With and without complete data

Distributions

Joint distribution:



Conditioning:



Conditioning: Renormalization:



Marginalization:

Factors:

Factor Definition:

A factor is a function, or a table. It takes a bunch of arguments.

A factor ϕ(X1,...,Xk)

ϕ:Val(X1,...,Xk)→R

Scope = {X1,...,Xk}



The scope of the CPD above is {G}.

Factor Operation:

Three types of operation: Factor Product, Factor Marginalization and Factor Reduction

Factor Product:



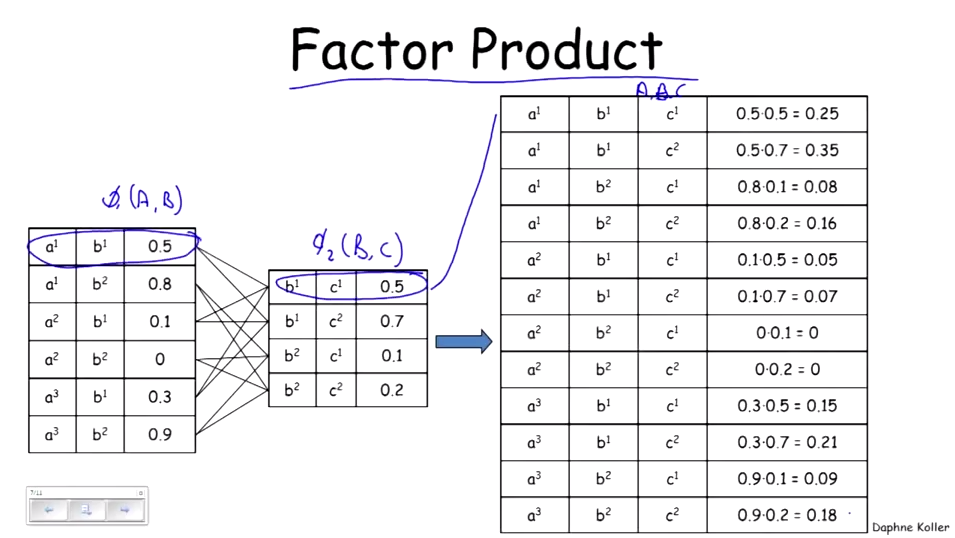
Factor Marginalization:



Factor Reduction:

Bayesian Network Fundamentals

Semantics & Factorization

Example: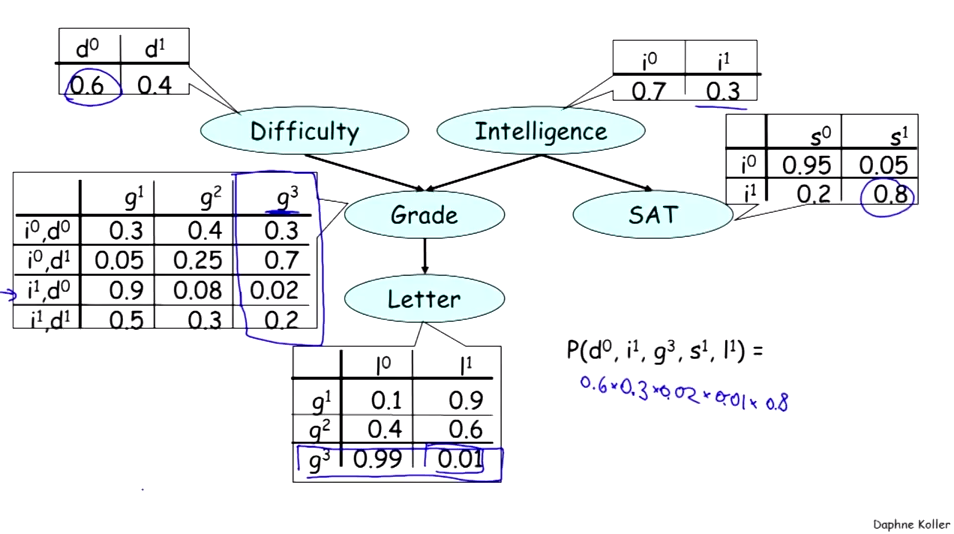



What is Bayesian Network:



Bayesian Network(BN) is a legal distribution:P≥0and∑P=1

Prove:



Let G be a graph overX1,...,Xn, we say P factorizes over G if P(X1,...,Xn)=∏iP(Xi∣ParG(Xi))

chromosome:染色体

genotype:基因型

phenotype:表现型

Reasoning Patterns

Causal Reasoning（因果推理）：从顶向下，以父节点或者祖先节点为条件。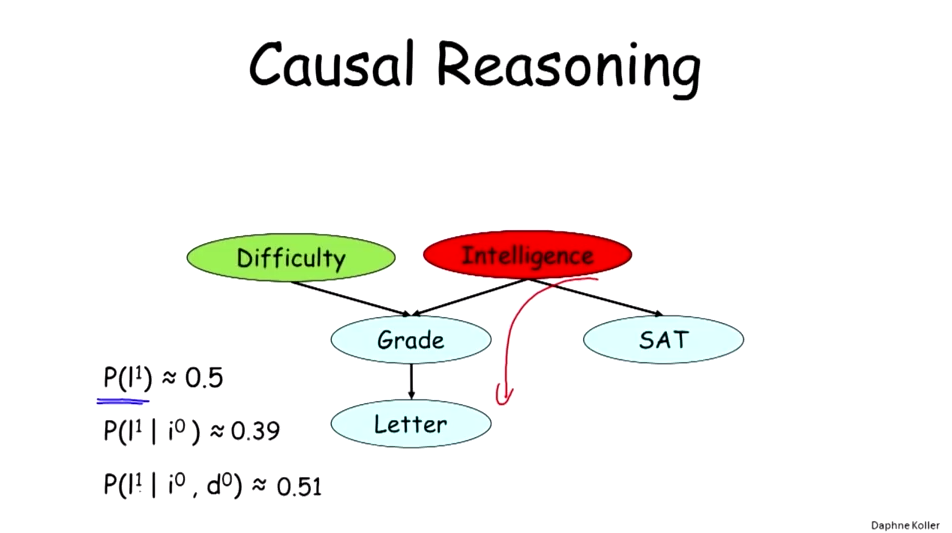



Evidential Reasoning（证据推理）：从下向上，以子孙节点为条件。



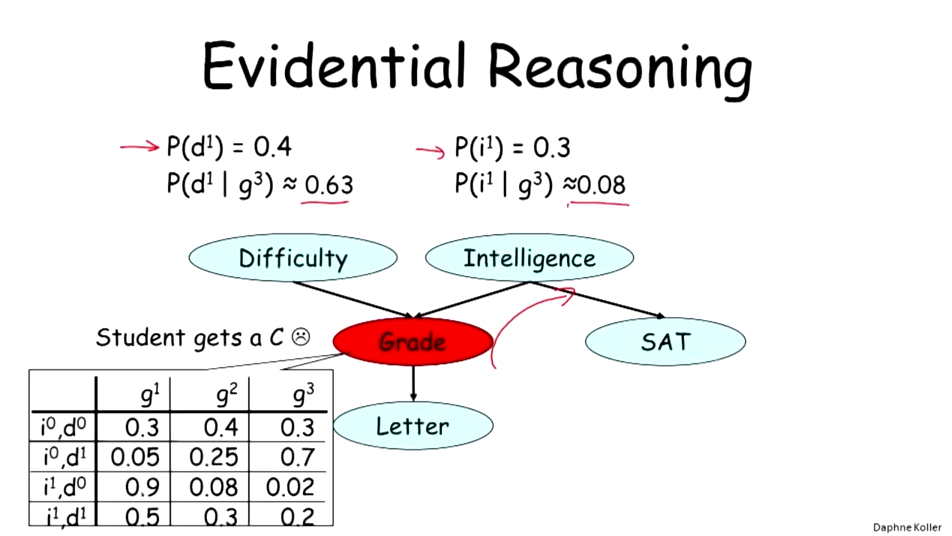
Intercausal Reasoning（又叫Mixed Reasoning，混合推理）：结合了因果推理和证据推理的推理方式。

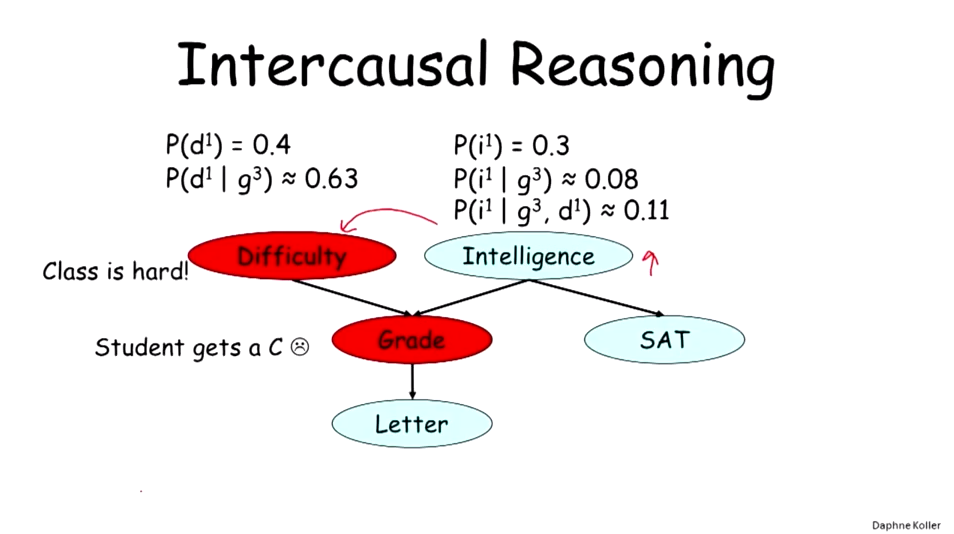
Flow of Probabilistic Influence

Two types:

When can X influence Y（condition on X changes beliefs about Y）？



Active Trail: A trail X1—...—Xnis active if it has no v-structures Xi−1→Xi←Xi+1.

When can X influence Y？ Given evidence about Z.



Active Trail: Atrail X1—...—Xnis active given Z if:

For any v-structure Xi−1→Xi←Xi+1we have that Xior one if its descendants belong to Z.

No other Xiis in Z.

Conditional Independence

Independence:

P⊨α⊥β means P satisfies α and β are independence.



Example:



Conditional Independence:



Example:



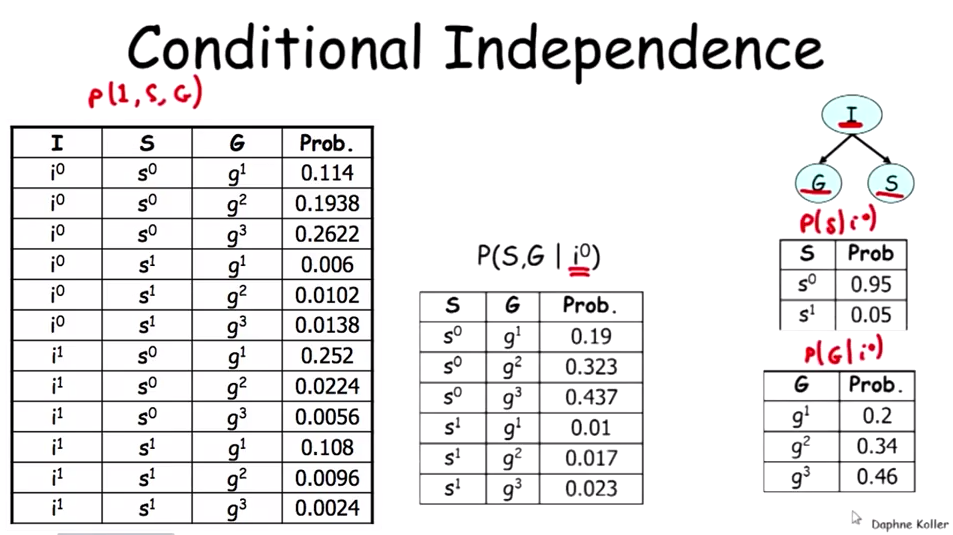
Notice:

Independence in Bayesian Networks

Question:

Factorization of a distribution P implies independencies that hold in P. If P factorizes over G, can we read these independencies from the structure of G?

Definition:

X and Y are d-separated in G given Z if there is no actvie trail in G between X and Y given Z. Notation: d−sepG(X,Y∣Z)

Theorem:

If P factorizes over G and d−sepG(X,Y∣Z), then P satisfies (X⊥Y∣Z)

Proof:



Question: What is ∑IP(I)(S∣I)?

Answer: P(S), this is a standard marginalization operation.

I-maps:

Notation: I(G)={(X⊥Y∣Z):d−sepG(X,Y∣Z)}

Explanation: I(G) is the set of independencies that are implicit in a graph G are all of the independent statements X is independent of Y given Z that correspond to d-separation statements within the graph.

Definition: If P satisfies I(G), we say that G is an I-map (independency map) of P.

Example:



Theorem:

If P factorizes over G, then G is an I-map for P.

If G is an I-map for P, then P factorizes over G.

Summary:

Naive Bayes

Application - Medical Diagnosis

Knowlege Engineering Example - SAMIAM

Template Models

ML-class Octave Tutorial