二叉排序树(Binary Sort Tree)

1、定义

二叉排序树（Binary Sort Tree）又称二叉查找(搜索)树（Binary Search Tree）。其定义为：二叉排序树或者是空树，或者是满足如下性质的二叉树：

① 若它的左子树非空，则左子树上所有结点的值均小于根结点的值；

② 若它的右子树非空，则右子树上所有结点的值均大于根结点的值；

③ 左、右子树本身又各是一棵二叉排序树。

上述性质简称二叉排序树性质(BST性质)，故二叉排序树实际上是满足BST性质的二叉树。

注意：

当用线性表作为表的组织形式时，可以有三种查找法。其中以二分查找效率最高。但由于二分查找要求表中结点按关键字有序，且不能用链表作存储结构，因此，当表的插入或删除操作频繁时，为维护表的有序性，势必要移动表中很多结点。这种由移动结点引起的额外时间开销，就会抵消二分查找的优点。也就是说，二分查找只适用于静态查找表。若要对动态查找表进行高效率的查找，可采用下二叉树或树作为表的组织形式。不妨将它们统称为树表。

2、特点

由BST性质可得：

（1） 二叉排序树中任一结点x，其左(右)子树中任一结点y(若存在)的关键字必小(大)于x的关键字。

（2） 二叉排序树中，各结点关键字是惟一的。

注意：

实际应用中，不能保证被查找的数据集中各元素的关键字互不相同，所以可将二叉排序树定义中BST性质(1)里的"小于"改为"大于等于"，或将BST性质(2)里的"大于"改为"小于等于"，甚至可同时修改这两个性质。

（3） 按中序遍历该树所得到的中序序列是一个递增有序序列。

【例】下图所示的两棵树均是二叉排序树，它们的中序序列均为有序序列：2，3，4，5，7，8。

3、存储结构

二叉树结构体定义;

typedef struct BiTNode
{
int data;
//结点数据
struct BiTNode *lChild,*rChild;
}BiTNode,*BiTree;

或如下定义：

typedef int KeyType；
//假定关键字类型为整数

typedef struct node {
KeyType key；
//关键字项
InfoType otherinfo；
//其它数据域，InfoType视应用情况而定，下面不处理它
struct node *lchild，*rchild；
//左右孩子指针
} BSTNode；
typedef BSTNode *BSTree；
//BSTree是二叉排序树的类型

4、二叉排序树运算

（1）二叉排序树的插入和生成

① 二叉排序树插入新结点的过程

在二叉排序树中插入新结点，要保证插入后仍满足BST性质。其插入过程是：

a、若二叉排序树T为空，则为待插入的关键字key申请一个新结点，并令其为根；

b、若二叉排序树T不为空，则将key和根的关键字比较：

(i)若二者相等，则说明树中已有此关键字key，无须插入。
(ii)若key<T→key，则将key插入根的左子树中。

(iii)若key>T→key，则将它插入根的右子树中。

子树中的插入过程与上述的树中插入过程相同。如此进行下去，直到将key作为一个新的叶结点的关键字插入到二叉排序树中，或者直到发现树中已有此关键字为止。

② 二叉排序树插入新结点的递归算法

③ 二叉排序树插入新结点的非递归算法

void InsertBST(BSTree *Tptr，KeyType key)
{ //若二叉排序树 *Tptr中没有关键字为key，则插入，否则直接返回
BSTNode *f，*p=*TPtr； //p的初值指向根结点
while(p){ //查找插入位置
if(p->key==key) return；//树中已有key，无须插入
f=p； //f保存当前查找的结点
p=(key<p->key)?p->lchild：p->rchild；
//若key<p->key，则在左子树中查找，否则在右子树中查找
} //endwhile
p=(BSTNode *)malloc(sizeof(BSTNode))；
p->key=key； p->lchild=p->rchild=NULL； //生成新结点
if(*TPtr==NULL) //原树为空
*Tptr=p； //新插入的结点为新的根
else //原树非空时将新结点关p作为关f的左孩子或右孩子插入
if(key<f->key)
f->lchild=p；
else f->rchild=p；
} //InsertBST

④ 二叉排序树的生成

二叉排序树的生成，是从空的二叉排序树开始，每输入一个结点数据，就调用一次插入算法将它插入到当前已生成的二叉排序树中。生成二叉排序树的算法如下：

BSTree CreateBST(void)
{ //输入一个结点序列，建立一棵二叉排序树，将根结点指针返回
BSTree T=NULL； //初始时T为空树
KeyType key；
scanf("％d"，&key)； //读人一个关键字
while(key){ //假设key=0是输人结束标志
InsertBST(&T，key)； //将key插入二叉排序树T
scanf("％d"，&key)；//读人下一关键字
}
return T； //返回建立的二叉排序树的根指针
} //BSTree

注意：

输入序列决定了二叉排序树的形态。

二叉排序树的中序序列是一个有序序列。所以对于一个任意的关键字序列构造一棵二叉排序树，其实质是对此关键字序列进行排序，使其变为有序序列。"排序树"的名称也由此而来。通常将这种排序称为树排序(Tree Sort)，可以证明这种排序的平均执行时间亦为O(nlgn)。

对相同的输入实例，树排序的执行时间约为堆排序的2至3倍。因此在一般情况下，构造二叉排序树的目的并非为了排序，而是用它来加速查找，这是因为在一个有序的集合上查找通常比在无序集合上查找更快。因此，人们又常常将二叉排序树称为二叉查找树。

（2）二叉排序树的删除

从二叉排序树中删除一个结点，不能把以该结点为根的子树都删去，并且还要保证删除后所得的二叉树仍然满足BST性质。

① 删除操作的一般步骤

a、进行查找

查找时，令p指向当前访问到的结点，parent指向其双亲（其初值为NULL）。若树中找不到被删结点则返回，否则被删结点是*p。

b、删去*p。

删*p时，应将*p的子树(若有)仍连接在树上且保持BST性质不变。按*p的孩子数目分三种情况进行处理。

② 删除*p结点的三种情况

a、*p是叶子(即它的孩子数为0)

无须连接*p的子树，只需将*p的双亲*parent中指向*p的指针域置空即可。

b、*p只有一个孩子*child

只需将*child和*p的双亲直接连接后，即可删去*p。

注意：

*p既可能是*parent的左孩子也可能是其右孩子，而*child可能是*p的左孩子或右孩子，故共有4种状态。

c、*p有两个孩子

先令q=p，将被删结点的地址保存在q中；然后找*q的中序后继*p，并在查找过程中仍用parent记住*p的双亲位置。*q的中序后继*p一定是*q的右子树中最左下的结点，它无左子树。因此，可以将删去*q的操作转换为删去的*p的操作，即在释放结点*p之前将其数据复制到*q中，就相当于删去了*q。。

③ 二叉排序树删除算法

分析：

　上述三种情况都能统一到情况(2)，算法中只需针对情况(2)处理即可。

　注意边界条件：若parent为空，被删结点*p是根，故删去*p后，应将child置为根。

算法：

void DelBSTNode(BSTree *Tptr，KeyType key)
{//在二叉排序树*Tptr中删去关键字为key的结点
BSTNode *parent=NUll，*p=*Tptr，*q，*child；
while(p){ //从根开始查找关键字为key的待删结点
if(p->key==key) break；//已找到，跳出查找循环
parent=p； //parent指向*p的双亲
p=(key<p->key)?p->lchild：p->rchild； //在关p的左或右子树中继续找
}
if(!p) return； //找不到被删结点则返回
q=p； //q记住被删结点*p
if(q->lchild&&q->rchild) //*q的两个孩子均非空，故找*q的中序后继*p
for(parent=q，p=q->rchild； p->lchild； parent=p，p=p=->lchild)；
//现在情况(3)已被转换为情况(2)，而情况(1)相当于是情况(2)中child=NULL的状况
child=(p->lchild)?p->lchild：p->rchild；//若是情况(2)，则child非空；否则child为空
if(!parent) //*p的双亲为空，说明*p为根，删*p后应修改根指针
*Tptr=child； //若是情况(1)，则删去*p后，树为空；否则child变为根
else{ //*p不是根，将*p的孩子和*p的双亲进行连接，*p从树上被摘下
if(p==parent->lchild) //*p是双亲的左孩子
parent->lchild=child； //*child作为*parent的左孩子
else parent->rchild=child； //*child作为 parent的右孩子
if(p!=q) //是情况(3)，需将*p的数据复制到*q
q->key=p->key； //若还有其它数据域亦需复制
} //endif
free(p)； /释放*p占用的空间
} //DelBSTNode

（3） 二叉排序树上的查找

① 查找递归算法

在二叉排序树上进行查找，和二分查找类似，也是一个逐步缩小查找范围的过程。

递归的查找算法：

/*在二叉排序树T上查找关键字为key的结点，成功时返回该结点位置，否则返回NUll*/
BSTNode *SearchBST(BSTree T，KeyType key)
{
if(T==NULL||key==T->key)
//递归的终结条件
return T；
//T为空，查找失败；否则成功，返回找到的结点位置
if(key<T->key)
return SearchBST(T->lchild，key)；
else
return SearchBST(T->rchild，key)；
//继续在右子树中查找
}

② 算法分析

在二叉排序树上进行查找时，若查找成功，则是从根结点出发走了一条从根到待查结点的路径。若查找不成功，则是从根结点出发走了一条从根到某个叶子的路径。

a、二叉排序树查找成功的平均查找长度

在等概率假设下，下面(a)图中二叉排序树查找成功的平均查找长度为



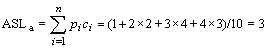
在等概率假设下，(b)图所示的树在查找成功时的平均查找长度为：

ASLb=(1+2+3+4+5+6+7+8+9+10)/10=5.5
注意：

与二分查找类似，和关键字比较的次数不超过树的深度。

b、在二叉排序树上进行查找时的平均查找长度和二叉树的形态有关

二分查找法查找长度为n的有序表，其判定树是惟一的。含有n个结点的二叉排序树却不惟一。对于含有同样一组结点的表，由于结点插入的先后次序不同，所构成的二叉排序树的形态和深度也可能不同

【例】下图(a)所示的树，是按如下插入次序构成的：

45，24，55，12，37，53，60，28，40，70
下图(b)所示的树，是按如下插入次序构成的：

12，24，28，37，40，45，53，55，60，70



在二叉排序树上进行查找时的平均查找长度和二叉树的形态有关：

① 在最坏情况下，二叉排序树是通过把一个有序表的n个结点依次插入而生成的，此时所得的二叉排序树蜕化为棵深度为n的单支树，它的平均查找长度和单链表上的顺序查找相同，亦是(n+1)/2。

② 在最好情况下，二叉排序树在生成的过程中，树的形态比较匀称，最终得到的是一棵形态与二分查找的判定树相似的二叉排序树，此时它的平均查找长度大约是lgn。

③ 插入、删除和查找算法的时间复杂度均为O(lgn)。

5、二叉排序树和二分查找的比较

就平均时间性能而言，二叉排序树上的查找和二分查找差不多。

就维护表的有序性而言，二叉排序树无须移动结点，只需修改指针即可完成插入和删除操作，且其平均的执行时间均为O(lgn)，因此更有效。二分查找所涉及的有序表是一个向量，若有插入和删除结点的操作，则维护表的有序性所花的代价是O(n)。当有序表是静态查找表时，宜用向量作为其存储结构，而采用二分查找实现其查找操作；若有序表里动态查找表，则应选择二叉排序树作为其存储结构。

6、平衡二叉树

　为了保证二叉排序树的高度为lgn，从而保证然二叉排序树上实现的插入、删除和查找等基本操作的平均时间为O(lgn)，在往树中插入或删除结点时，要调整树的形态来保持树的"平衡。使之既保持BST性质不变又保证树的高度在任何情况下均为O(lgn)，从而确保树上的基本操作在最坏情况下的时间均为O(lgn)。

注意：

　 ①平衡二叉树(Balanced Binary Tree)是指树中任一结点的左右子树的高度大致相同。

　②任一结点的左右子树的高度均相同(如满二叉树)，则二叉树是完全平衡的。通常，只要二叉树的高度为O(1gn)，就可看作是平衡的。

　③平衡的二叉排序树指满足BST性质的平衡二叉树。

　④AVL树中任一结点的左、右子树的高度之差的绝对值不超过1。在最坏情况下，n个结点的AVL树的高度约为1.44lgn。而完全平衡的二叉树度高约为lgn，AVL树是接近最优的。