排序算法(二)堆排序
2016-04-27 01:04
417 查看
一、选择排序的问题
如果有n个数排序,简单排序需要选取一个极值(最大值或者最小值)需要比较n-1次。但是,每一轮比较并没有把以前比较过的结果保存下来,导致下一轮比较的时候会有比较过的数据继续比较大小,这其实影响了效率,做了很多无用功。
堆排序是对简单选择排序的改进。
堆是一种数据结构,是用完全二叉树构建的大顶堆或者小顶堆,有的称为大根堆和小根堆。
二、堆排序的准备知识
1、二叉树
二叉树是至多存在两个子树的树结构。
二叉树的每一个结点度数不超过2(至多2棵子树)
2、深度
根结点为第一层,根的子结点为第二层,第二层的子结点为第三层,以此类推。
树中结点的最大层次称为该树的深度或高度。
3、满二叉树
一棵二叉树的所有分支结点都存在左子树和右子树,并且所有叶子结点只存在在最下面一层。
同样深度二叉树中,满二叉树结点最多。
k为深度(1≤k≤n),则结点总数为2^k-1
如下图,一个深度为4的15个结点的满二叉树:
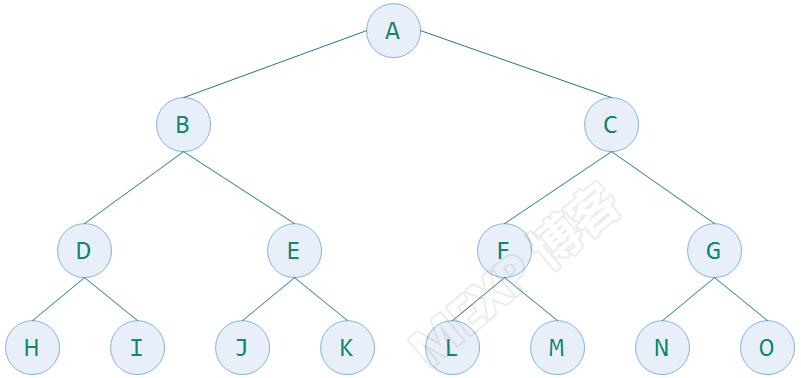
4、完全二叉树(Complete Binary Tree)
若二叉树的深度为k,二叉树的层数从1到k-1层的结点数都达到了最大个数,在第k层的所有结点都集中在最左边,这就是完全二叉树。
完全二叉树由满二叉树引出。
满二叉树一定是完全二叉树,但完全二叉树不是满二叉树。
k为深度(1≤k≤n),则结点总数最大值为2^k-1,当达到最大值的时候就是满二叉树。
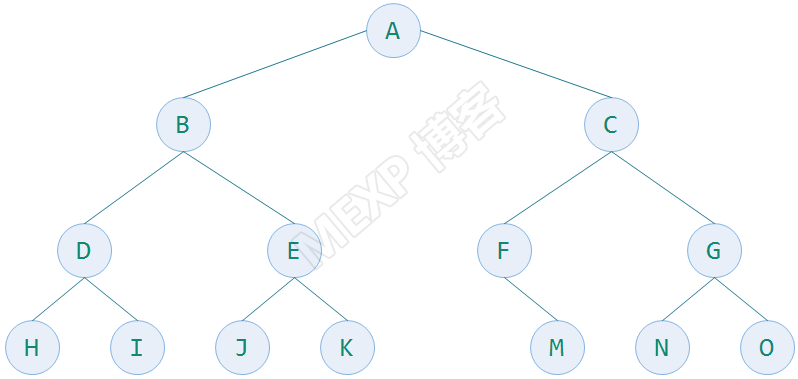
举例,下面几个图都是一个完全二叉树,最下一层的叶子结点都连续的集中在左边
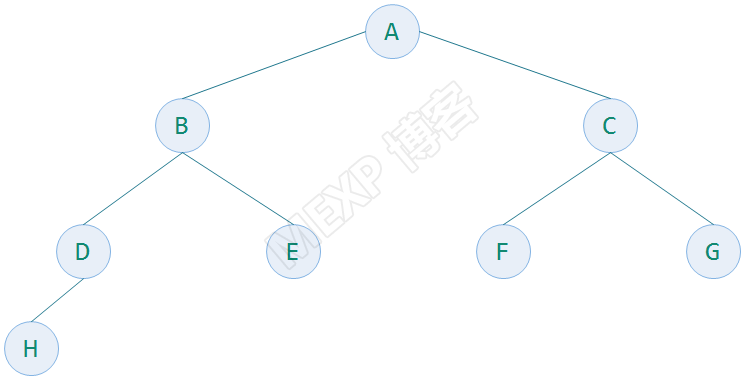
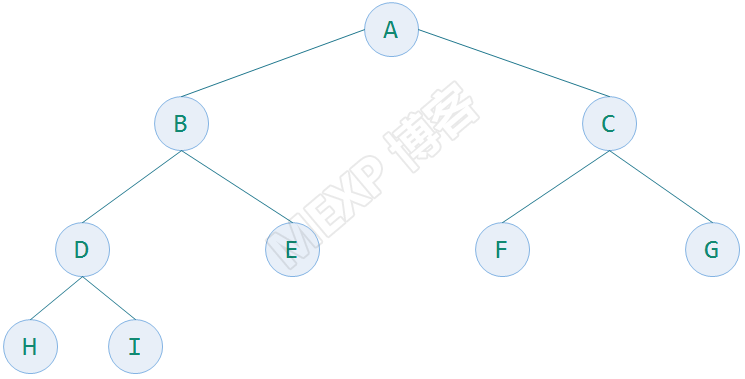
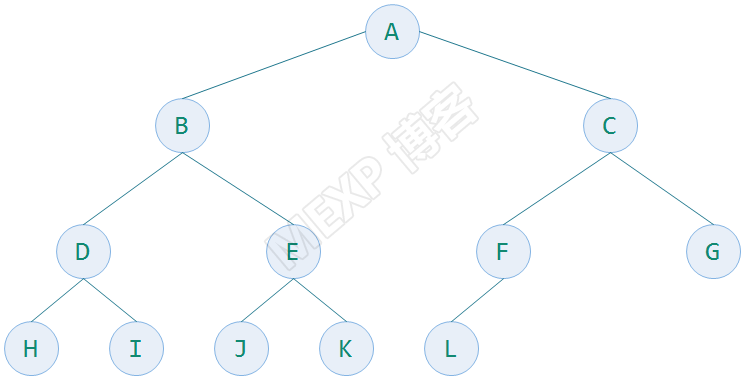
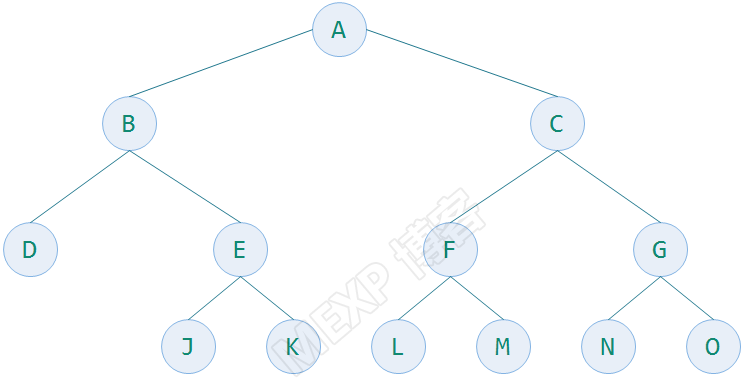
下面的图就不是完全二叉树,因为它的结点在最下一层不连续
5、大顶堆和小顶堆
使用完全二叉树来构建的数据结构。
(1)大顶堆
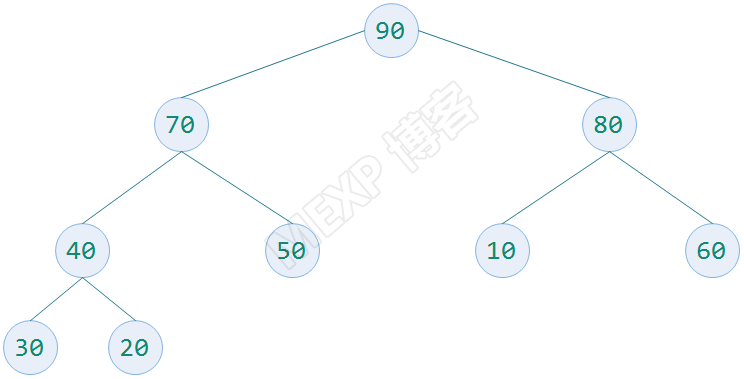
首先上图必须是一个完全二叉树,同时要求每一个非叶子结点的值都要大于等于它的所有子结点的值。
(2)小顶堆
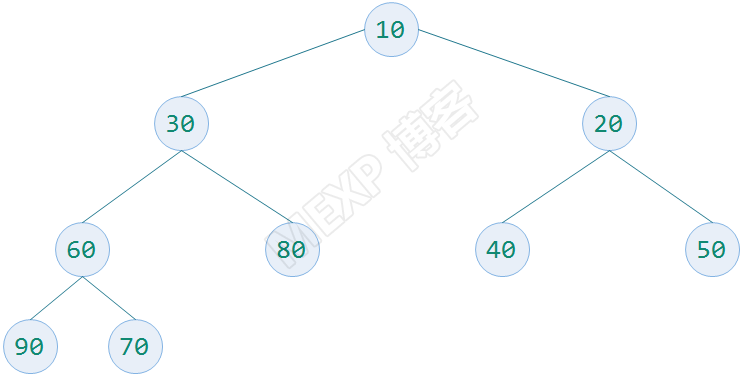
小顶堆也必须是一个完全二叉树,同时要求每一个非叶子结点的值都要小于等于它的所有子结点的值。
三、堆排序(Heap Sort)
有了上面的基础知识,就可以开始堆排序了,本次测试使用大顶堆排序
(一)算法思路
1、构建二叉树
将待排序的数字放在完全二叉树中。由于使用了完全二叉树,比较方便的方法是使用 顺序存储 来描述这个完全二叉树,也就是使用一位数组来表示完全二叉树。
假设待排序的数字为{30,20,80,40,50,10,60,70,90},二叉树表示如下:
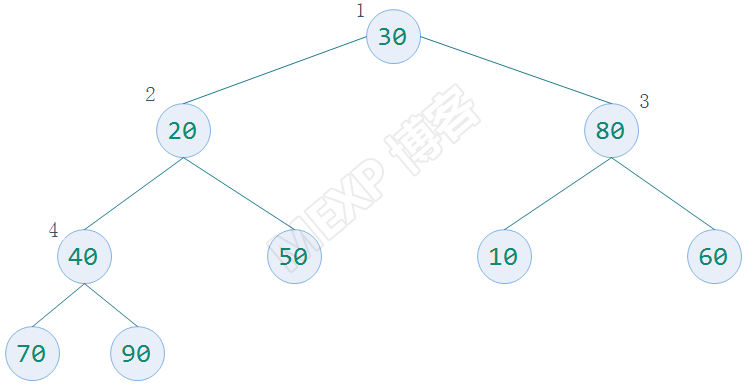
为了计算方便,使用下面的数组表示{0,30,20,80,40,50,10,60,70,90}。上图中的序号正好是数组的下标。
2、构建大顶堆
(1)核心算法
选择好起始的节点A,让这个节点与其子结点比较。
假设A有两个子结点B和C,如果子结点中的最大值大于节点A的值,则这个最大值节点和节点A交换位置。
假设A只有一个子结点B,如果B的值大于节点A的值,则交换位置。这种一个子结点的情况是上面的2个子结点的简化。
如果交换后,在新的位置上节点A还是有子结点C和D,那么还是要重复上面的过程,让结点A和结点C、结点D比较。
(2)起点的选择
构建大顶堆,从哪一个节点开始比较呢?
简单来说,从完全二叉树的最下一层的最右边叶子结点的父节点开始。
上图中是从第三层左一结点开始。
上面为了计算方便,数组特殊构造了,由此有以下的关系。
父子结点关系:父结点的下标为i,子结点的下标为2i和2i+1
起始结点和总数n的关系:n就对应最后的叶子结点的下标。因为子结点2i或者(2i+1)计算父结点下标,2i/2或者(2i+1)/2都等于i,所以n/2就是起点的下标。
(3)下一个节点的选择
比较完后,寻找下一个节点继续比较。从当前比较节点向左找兄弟结点,如果这一层找完了,就找上一层最右边结点,直至找到根结点。
构建大顶堆完成后,树结构如下图
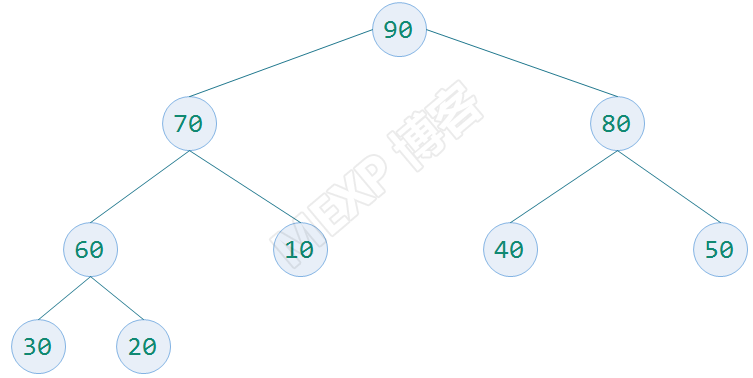
3、排序
这是一个迭代的过程。因为使用了大顶堆,每次交换都有很多结点不需要动,这充分体现了,保留了以前排序的结果的思想。
(1)交换大顶堆的根结点和最后一个叶子结点,那么最后一个叶子结点就是最大值,将这个叶子节点排除在排序的节点之外(因为这就是每次找到的最大值)。
(2)从根结点开始(新的根结点),重新调整为大顶堆后,重复上一步。
每一轮从新的根结点调整为大顶堆的过程和上述构建大顶堆的核心算法是一样的,因为用的同一个函数,不过就是起点选择不同,构建大顶堆过程是从n/2开始倒着调整,而堆排序的时候始终从根结点开始。
(二)代码实现(Java)
(三)总结
1、时间复杂度
假设结点数为n,完全二叉树的深度为k
在构建堆的过程中,因为我们是完全二叉树从最下层最右边的非终端结点开始构建,将它与其孩子进行比较和若有必要的互换,对于每个非终端结点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为O(n)。
在正式排序时,第i次取堆顶记录重建堆需要用O(logn)的时间,并且需要循环取n-1次堆顶记录,因此,重建堆的时间复杂度为O(nlogn)。
所以总体来说,堆排序的时间复杂度为O(nlogn)。由于堆排序对原始记录的排序状态并不敏感,因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。
2、空间复杂度
就使用了一个交换用的空间,空间复杂度为O(1)
3、稳定性
不稳定的排序方法。
参考 http://baike.baidu.com/view/157305.htm 《大话数据结构》
如果有n个数排序,简单排序需要选取一个极值(最大值或者最小值)需要比较n-1次。但是,每一轮比较并没有把以前比较过的结果保存下来,导致下一轮比较的时候会有比较过的数据继续比较大小,这其实影响了效率,做了很多无用功。
堆排序是对简单选择排序的改进。
堆是一种数据结构,是用完全二叉树构建的大顶堆或者小顶堆,有的称为大根堆和小根堆。
二、堆排序的准备知识
1、二叉树
二叉树是至多存在两个子树的树结构。
二叉树的每一个结点度数不超过2(至多2棵子树)
2、深度
根结点为第一层,根的子结点为第二层,第二层的子结点为第三层,以此类推。
树中结点的最大层次称为该树的深度或高度。
3、满二叉树
一棵二叉树的所有分支结点都存在左子树和右子树,并且所有叶子结点只存在在最下面一层。
同样深度二叉树中,满二叉树结点最多。
k为深度(1≤k≤n),则结点总数为2^k-1
如下图,一个深度为4的15个结点的满二叉树:

4、完全二叉树(Complete Binary Tree)
若二叉树的深度为k,二叉树的层数从1到k-1层的结点数都达到了最大个数,在第k层的所有结点都集中在最左边,这就是完全二叉树。
完全二叉树由满二叉树引出。
满二叉树一定是完全二叉树,但完全二叉树不是满二叉树。
k为深度(1≤k≤n),则结点总数最大值为2^k-1,当达到最大值的时候就是满二叉树。
举例,下面几个图都是一个完全二叉树,最下一层的叶子结点都连续的集中在左边



下面的图就不是完全二叉树,因为它的结点在最下一层不连续


5、大顶堆和小顶堆
使用完全二叉树来构建的数据结构。
(1)大顶堆

首先上图必须是一个完全二叉树,同时要求每一个非叶子结点的值都要大于等于它的所有子结点的值。
(2)小顶堆

小顶堆也必须是一个完全二叉树,同时要求每一个非叶子结点的值都要小于等于它的所有子结点的值。
三、堆排序(Heap Sort)
有了上面的基础知识,就可以开始堆排序了,本次测试使用大顶堆排序
(一)算法思路
1、构建二叉树
将待排序的数字放在完全二叉树中。由于使用了完全二叉树,比较方便的方法是使用 顺序存储 来描述这个完全二叉树,也就是使用一位数组来表示完全二叉树。
假设待排序的数字为{30,20,80,40,50,10,60,70,90},二叉树表示如下:

为了计算方便,使用下面的数组表示{0,30,20,80,40,50,10,60,70,90}。上图中的序号正好是数组的下标。
2、构建大顶堆
(1)核心算法
选择好起始的节点A,让这个节点与其子结点比较。
假设A有两个子结点B和C,如果子结点中的最大值大于节点A的值,则这个最大值节点和节点A交换位置。
假设A只有一个子结点B,如果B的值大于节点A的值,则交换位置。这种一个子结点的情况是上面的2个子结点的简化。
如果交换后,在新的位置上节点A还是有子结点C和D,那么还是要重复上面的过程,让结点A和结点C、结点D比较。
(2)起点的选择
构建大顶堆,从哪一个节点开始比较呢?
简单来说,从完全二叉树的最下一层的最右边叶子结点的父节点开始。
上图中是从第三层左一结点开始。
上面为了计算方便,数组特殊构造了,由此有以下的关系。
父子结点关系:父结点的下标为i,子结点的下标为2i和2i+1
起始结点和总数n的关系:n就对应最后的叶子结点的下标。因为子结点2i或者(2i+1)计算父结点下标,2i/2或者(2i+1)/2都等于i,所以n/2就是起点的下标。
(3)下一个节点的选择
比较完后,寻找下一个节点继续比较。从当前比较节点向左找兄弟结点,如果这一层找完了,就找上一层最右边结点,直至找到根结点。
构建大顶堆完成后,树结构如下图

3、排序
这是一个迭代的过程。因为使用了大顶堆,每次交换都有很多结点不需要动,这充分体现了,保留了以前排序的结果的思想。
(1)交换大顶堆的根结点和最后一个叶子结点,那么最后一个叶子结点就是最大值,将这个叶子节点排除在排序的节点之外(因为这就是每次找到的最大值)。
(2)从根结点开始(新的根结点),重新调整为大顶堆后,重复上一步。
每一轮从新的根结点调整为大顶堆的过程和上述构建大顶堆的核心算法是一样的,因为用的同一个函数,不过就是起点选择不同,构建大顶堆过程是从n/2开始倒着调整,而堆排序的时候始终从根结点开始。
(二)代码实现(Java)
package heapsort;
import java.util.Arrays;
import java.util.HashSet;
public class HeapSort {
// 为了计算取下标方便,增加一个0在数组的首位
// 待比较数个数n为9
//public static int[] origin = new int[]{0,30,20,80,40,50,10,60,70,90};
public static int[] origin = new int[]{0,50,10,90,30,70,40,80,60,20};
// indexSet数组记录每一次变化的结点的索引,仅是为了方便观察
private static HashSet<Integer> indexSet = new HashSet<Integer>();
public static void main(String[] args) {
int total = origin.length-1;
System.out.println("Unsorted: "+Arrays.toString(origin));
// 构建大顶堆
for (int i = total/2,k=1; i >= 1; i--,k++) {
heapAdjust(total,i,origin);
// 打印每一次调整的结果及交换的下标
System.out.println(k + "\t" + Arrays.toString(origin) + " " + Arrays.toString(indexSet.toArray()));
}
System.out.println();
// 堆排序
for (;total>1;) {
System.out.println(total);
// 交换根结点和最后一个叶子结点
swap(1, total, origin);
System.out.println("Swapped: " + Arrays.toString(origin));
// 总数减1,因为最后一个叶子结点现在是最大值,要排除在排序数字之外
total--;
if (total==2 && origin[total]>=origin[total-1]) {
// 改进的地方:如果只剩2个结点比较,且第二个结点大于等于根结点,没有必要再调整了,可以直接退出了
break;
}
heapAdjust(total,1,origin);
// 打印每一次调整的结果及交换的下标
System.out.println("Changed: " + Arrays.toString(origin) + " " + Arrays.toString(indexSet.toArray()));
System.out.println();
}
System.out.println("Sorted: "+Arrays.toString(origin));
}
/**
* adjustHeap 调整为大顶堆结构
* @param n 待比较数的个数
* @param index 每次比较的结点下标
* @param array 待比较的数组
*/
public static void heapAdjust(int n,int index,int [] array){
indexSet.clear();
int maxChildrenIndex;
for (int i = 2*index; i <= n; i = index<<1) {
maxChildrenIndex = i;
if (i<n && array[i]<array[i+1]) {
// 小于n说明还有右边的结点,选出最大子结点的下标
maxChildrenIndex=i+1;
}
// 等于n,说明只有一个子结点;小于n,同时左边结点大于右边结点,这两种情况maxindex都不用改变了。
if (array[maxChildrenIndex]>array[index]) {
swap(index, maxChildrenIndex, array);
// 记录交换的结点index,便于观察
indexSet.add(index);
indexSet.add(maxChildrenIndex);
// 调整后,需要重设比较的起始结点,看这个结点和它的子结点是否还要需要调整
index = maxChildrenIndex;
}
else {
break;
}
}
}
public static void swap(int index1,int index2,int [] array){
try {
int temp = origin[index1];
origin[index1] = origin[index2];
origin[index2] = temp;
} catch (Exception e) {
throw new ArrayIndexOutOfBoundsException();
}
}
}(三)总结
1、时间复杂度
假设结点数为n,完全二叉树的深度为k
在构建堆的过程中,因为我们是完全二叉树从最下层最右边的非终端结点开始构建,将它与其孩子进行比较和若有必要的互换,对于每个非终端结点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为O(n)。
在正式排序时,第i次取堆顶记录重建堆需要用O(logn)的时间,并且需要循环取n-1次堆顶记录,因此,重建堆的时间复杂度为O(nlogn)。
所以总体来说,堆排序的时间复杂度为O(nlogn)。由于堆排序对原始记录的排序状态并不敏感,因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。
2、空间复杂度
就使用了一个交换用的空间,空间复杂度为O(1)
3、稳定性
不稳定的排序方法。
参考 http://baike.baidu.com/view/157305.htm 《大话数据结构》
相关文章推荐
- AVL树-自平衡二叉查找树(Java实现)
- C语言二叉树的非递归遍历实例分析
- 使用C语言构建基本的二叉树数据结构
- 一波二叉树遍历问题的C++解答实例分享
- 举例讲解C语言程序中对二叉树数据结构的各种遍历方式
- C++非递归队列实现二叉树的广度优先遍历
- PHP实现的线索二叉树及二叉树遍历方法详解
- C#使用前序遍历、中序遍历和后序遍历打印二叉树的方法
- C#非递归先序遍历二叉树实例
- C++将二叉树转为双向链表及判断两个链表是否相交
- C++非递归建立二叉树实例
- C语言实现找出二叉树中某个值的所有路径的方法
- C++实现二叉树遍历序列的求解方法
- C语言实现二叉树遍历的迭代算法
- C++实现查找二叉树中和为某一值的所有路径的示例
- 用C语言判断一个二叉树是否为另一个的子结构
- C++实现二叉树非递归遍历方法实例总结
- C++二叉树结构的建立与基本操作
- 深入遍历二叉树的各种操作详解(非递归遍历)
- JavaScript数据结构和算法之二叉树详解
