poj2409 Let it Bead(polyal原理)
2016-04-26 17:46
411 查看
Let it Bead
Description
"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent
of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It's a good thing that bracelets can have different lengths and need not be made of beads of one
color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced.
A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate
the number of different bracelets that can be made.
Input
Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine,
cs<=32, i.e. their product does not exceed 32.
Output
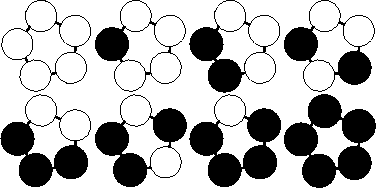
For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.
Sample Input
Sample Output
问,一串由n个珠子组成的项链,用c种颜色涂染,问能形成多少种不同项链,由旋转而得到的为同一种,反转而来的也为同一种。
polyal原理:
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std;
int m,n,j,k,l,i,p;
int gcd(int a,int b)
{
if(b==0)
return a;
return gcd(b,a%b);
}
void polyal()
{
int i,c,s=0,t;
for(i=0;i<n;i++)
{
c=gcd(n,i);
s+=(int)pow((double)m,(double)c);
}
if(n&1)
{
c=(n+1)/2;
t=(int)pow((double)m,(double)c);
s+=t*n;
}
else
{
c=n/2;
t=(int)pow((double)m,(double)c);
s+=(n/2)*t;
t*=m;
s+=(n/2)*t;
}
printf("%d\n",s/(2*n));
}
int main()
{
while(scanf("%d%d",&m,&n),m+n)
{
polyal();
}
}
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 5367 | Accepted: 3587 |
"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent
of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It's a good thing that bracelets can have different lengths and need not be made of beads of one
color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced.
A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate
the number of different bracelets that can be made.
Input
Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine,
cs<=32, i.e. their product does not exceed 32.
Output

For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.
Sample Input
1 1 2 1 2 2 5 1 2 5 2 6 6 2 0 0
Sample Output
1 2 3 5 8 1321
问,一串由n个珠子组成的项链,用c种颜色涂染,问能形成多少种不同项链,由旋转而得到的为同一种,反转而来的也为同一种。
polyal原理:
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std;
int m,n,j,k,l,i,p;
int gcd(int a,int b)
{
if(b==0)
return a;
return gcd(b,a%b);
}
void polyal()
{
int i,c,s=0,t;
for(i=0;i<n;i++)
{
c=gcd(n,i);
s+=(int)pow((double)m,(double)c);
}
if(n&1)
{
c=(n+1)/2;
t=(int)pow((double)m,(double)c);
s+=t*n;
}
else
{
c=n/2;
t=(int)pow((double)m,(double)c);
s+=(n/2)*t;
t*=m;
s+=(n/2)*t;
}
printf("%d\n",s/(2*n));
}
int main()
{
while(scanf("%d%d",&m,&n),m+n)
{
polyal();
}
}
相关文章推荐
- 初学ACM - 组合数学基础题目PKU 1833
- POJ ACM 1001
- POJ ACM 1002
- 1611:The Suspects
- POJ1089 区间合并
- POJ 2635 The Embarrassed Cryptographe
- POJ 3292 Semi-prime H-numbers
- POJ 2773 HAPPY 2006
- POJ 3090 Visible Lattice Points
- POJ-2409-Let it Bead&&NYOJ-280-LK的项链
- POJ-1695-Magazine Delivery-dp
- POJ1523 SPF dfs
- POJ-1001 求高精度幂-大数乘法系列
- POJ-1003 Hangover
- POJ-1004 Financial Management
- 用单调栈解决最大连续矩形面积问题
- 2632 Crashing Robots的解决方法
- 1573 Robot Motion (简单题)
- POJ 1200 Crazy Search(简单哈希)
- 【高手回避】poj3268,一道很水的dijkstra算法题
