平衡二叉树（AVL树）的基本操作

平衡二叉树关于树的深度是平衡的，具有较高的检索效率。平衡二叉树或是一棵空树，或是具有下列性质的二叉排序树：其左子树和右子树都是平衡二叉树，而且左右子树深度之差绝对值不超过1. 由此引出了平衡因子（balance factor）的概念，bf定义为该结点的左子树的深度减去右子树的深度（有些书是右子树深度减去左子树深度，我是按照左子树减去右子树来计算的，下面的代码也是这样定义的），所以平衡二叉树的结点的平衡因子只可能是 -1，0，1 ，某个结点的平衡因子绝对值大于1，该二叉树就不平衡。

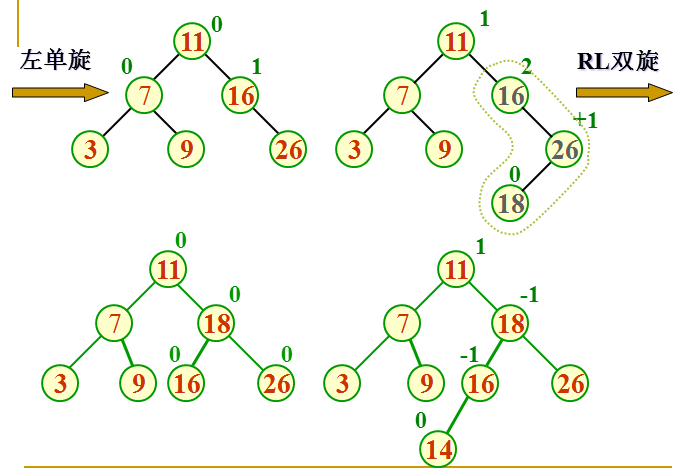
平衡二叉树在出现不平衡状态的时候，要进行平衡旋转处理，有四种平衡旋转处理（单向右旋处理，单向左旋处理，双向旋转（先左后右）处理，双向旋转（先右后左）处理），归根到底是两种（单向左旋处理和单向右旋处理）。

代码中，由于调试每次都输入数据，太麻烦，我就将输入屏蔽了，直接用一组数据初始化，在Create_AVL中可以修改。下面是删除结点时要考虑的。

/*---------------------------------------------------------
/ 从树中删除一个节点后，要保证删后的树还是一棵平衡二叉树，
/ 删除前，首先是在树中查找是否有这个结点，用p指向该结点，
/ 用f指向p的双亲结点，这个结点在树中的位置有下面四种情况:
/
/ 1:如果p指向的结点是叶子结点，那么直接将f指针的左子树或者
/ 右子树置空，然后删除p结点即可。
/
/ 2:如果p指向的结点是只有左子树或右子树，那么只需要让p结点
/ 原来在f中的位置(左子树或右子树)用p的子树代替即可。
/ 代替后，要修改f的平衡因子，在失去平衡的时候，要调用相应的
/ 做平衡旋转或右平衡旋转进行恢复.
/
/ 3:如果p所指向的结点是根节点，那么直接将根节点置空
/
/ 4:如果p所指向的结点左右子树都非空，为了删除p后原序列的顺
/ 序不变，就需要在原序列中先找出p的直接前驱(或者直接后继)
/ 结点用那个结点的值来代替p结点的值，然后再删掉那个直接前
/ 驱(或者直接后继)结点。
/ 其中s指向的是要删除的结点，也就是p的直接前驱，q指向的是
/ s的双亲结点，此时，应该看s的平衡因子，在会出现失去平衡的
/ 情况时，就要根据实际情况采用左平衡旋转或是右平衡旋转，让
/ 树恢复平衡，这点和插入操作时是相对应的。
/
/ 在中序遍历序列中找结点的直接前驱的方法是顺着结点的左孩子
/ 的右链域开始，一直到结点右孩子为空为止。
/---------------------------------------------------------*/

源代码：

Tree.h文件

#include <iostream>
#include <stack>
#include <queue>

using namespace std;

const int LH = 1; // 左子树比右子树高1
const int EH = 0; // 左右子树一样高
const int RH = -1;// 右子树比左子树高1
const int MAX_NODE_NUM = 20; // 结点数目上限

class AVL_tree;

class AvlNode{
int data;
int bf;   // 平衡因子
AvlNode *lchild;
AvlNode *rchild;
friend class AVL_Tree;

};

class AVL_Tree{

public:
int Get_data(AvlNode *p);

void Create_AVI(AvlNode *&T);

//若在平衡二叉树中不存在结点值和num一样大小的结点
//则插入值为num的新结点，并返回true
//若因为插入而使得二叉排序树失去平衡，则做平衡旋转处理
//taller反映树是否长高
bool Insert_Avl(AvlNode *&T,int num,bool &taller);
// 以p为根节点的二叉排序树进行单向左旋处理
void L_Rotate(AvlNode *&p);

// 以p为根节点的二叉排序树进行单向右旋处理
void R_Rotate(AvlNode *&p);

// 以T为根节点的二叉排序树进行左平衡处理
void Left_Balance(AvlNode *&T);

// 以T为根节点的二叉排序树进行右平衡旋转处理
void Right_Balance(AvlNode *&T);

// 中序遍历
void InOrder_Traverse(AvlNode *T);
// 层次遍历
void Level_Traverse(AvlNode *T);
void Delete_AVL(AvlNode *&T,int num);
bool Search_Avl(AvlNode *T,int num,AvlNode *&f,AvlNode *&p);
};
int AVL_Tree::Get_data(AvlNode *p){
return p->data;

}

void AVL_Tree::Create_AVI(AvlNode *&T){

cout<<"输入平衡二叉树的元素，输入-1代表结束输入:"<<endl;
int num[MAX_NODE_NUM] = {16,3,7,11,9,26,18,14,15};
int i=0;
//int a;
/*while(cin>>a && a!=-1){
num[i] = a;
i++;
}

if(num[0] == -1){
cout<<"平衡二叉树为空."<<endl;
T = NULL;
return;
}*/

//int k = i;
int k = 9;
bool taller = false;

for(i=0;i<k;i++){
Insert_Avl(T,num[i],taller);

}
cout<<"___建树完成___"<<endl;

}

//若在平衡二叉树中不存在结点值和num一样大小的结点
//则插入值为num的新结点，并返回true
//若因为插入而使得二叉排序树失去平衡，则做平衡旋转处理
//taller反映树是否长高
bool AVL_Tree::Insert_Avl(AvlNode *&T,int num,bool &taller){

if(!T){

// 插入新节点，树长高，taller为true
T = new AvlNode();
T->data = num;
T->lchild = T->rchild = NULL;
T->bf = EH;
taller = true;

}else{
// 不重复插入
if(num == T->data){
taller = false;
cout<<num<<"已经在树中"<<endl;
return false;
}

// 继续在T的左子树上进行搜索
if(num < T->data){

// 在左子树上插入不成功
if(!Insert_Avl(T->lchild,num,taller)){
return false;
}
// 已插入T的左子树，且左子树长高
if(taller){
switch(T->bf){
// 插入前左子树高
case LH:
Left_Balance(T);
taller = false;
break;
// 插入前左右子树等高
case EH:
T->bf = LH;
taller = true;
break;
// 插入前右子树高,插入左子树后等高
case RH:
T->bf = EH;
taller = false;
break;

}
}

}else{
// 在T的右子树中继续搜索
if(!Insert_Avl(T->rchild,num,taller)){
return false;
}
if(taller){
switch(T->bf){
//插入前左子树比右子树高，现在插入T的右子树后，左右子树等高
case LH:
T->bf = EH;
taller = false;
break;
//插入前左右子树等高，现在插入后，右子树比左子树高
case EH:
T->bf = RH;
taller = true;
break;
//插入前右子树比坐子树高，插入后，排序树失去平衡，需要进行右平衡处理
case RH:
Right_Balance(T);
taller = false;
break;
}
}
}
}
return true;

}

// 以p为根节点的二叉排序树进行单向左旋处理
void AVL_Tree::L_Rotate(AvlNode *&p){

AvlNode *rc = p->rchild;
p->rchild = rc->lchild;
rc->lchild = p;
p = rc;

}

// 以p为根节点的二叉排序树进行单向右旋处理
void AVL_Tree::R_Rotate(AvlNode *&p){

AvlNode *lc = p->lchild;
p->lchild = lc->rchild;
lc->rchild = p;
p = lc;

}

// 以T为根节点的二叉排序树进行左平衡处理,先左旋再右旋
void AVL_Tree::Left_Balance(AvlNode *&T){

AvlNode *lc,*rd;
lc = T->lchild;
switch(lc->bf){
// 先根据最后结果修改平衡因子，再旋转，如果先旋转，则指针已发生变化，后续的平衡因子，修改不便
case LH:
// 新节点插在T的左孩子的左子树上，做单向右旋处理
T->bf = lc->bf = EH;
R_Rotate(T);

break;

case RH:
// 新节点插在T的左孩子的右子树上，要进行双旋平衡处理（先左后右）
rd = lc->rchild;

switch(rd->bf){
// LH和RH是针对调整的结构中的最后一个节点不是叶子节点的情况
case LH:
T->bf = RH;
lc->bf = EH;
//	cout<<"Left LH data:"<<rd->data<<endl;
break;
// 从不稳定节点开始到新插入的节点成<号型，此时的新插入节点bf为0
// 针对不稳定结构的最后一个节点是叶子节点的情况
case EH:
T->bf = lc->bf = EH;
//	cout<<"Left EH data:"<<rd->data<<endl;
break;
case RH:
T->bf = EH;
lc->bf = RH;
//		cout<<"Left RH data:"<<rd->data<<endl;
break;

}
rd->bf = EH;
// 先对左子树进行左单旋
L_Rotate(T->lchild);
// 再对整颗数进行右单旋
R_Rotate(T);
break;

}

}

// 以T为根节点的二叉排序树进行右平衡旋转处理，先右旋再左旋
void AVL_Tree::Right_Balance(AvlNode *&T){

AvlNode *rc,*ld;
rc = T->rchild;
switch(rc->bf){
// 新节点插在右孩子的右子树上，进行单向左旋
case RH:
T->bf = rc->bf = EH;
L_Rotate(T);
break;
// 新节点插在T的右孩子的左子树上，要进行右平衡处理（先右再左）
case LH:
ld = rc->lchild;
switch(ld->bf){
// LH和RH是针对调整的结构中的最后一个节点不是叶子节点的情况
case LH:
T->bf = EH;
rc->bf = RH;
//		cout<<"Right LH data:"<<ld->data<<endl;
break;
// 针对不稳定结构的最后一个节点是叶子节点的情况
case EH:
T->bf = rc->bf = EH;
//		cout<<"Right EH data:"<<ld->data<<endl;
break;
case RH:
T->bf = LH;
rc->bf = EH;
//	cout<<"Right RH data:"<<ld->data<<endl;
break;

}
ld->bf = EH;
// 对右子树进行右单旋
R_Rotate(T->rchild);
// 对整棵树进行左单旋
L_Rotate(T);
break;
}
}

// 中序遍历
void AVL_Tree::InOrder_Traverse(AvlNode *T){

stack<AvlNode *> s;
AvlNode *p = T;

while(p || !s.empty()){
// 只要指针不空，一直入栈
if(p){
s.push(p);
p = p->lchild;
// 当到达叶子节点，再往下指针为空时，将栈顶弹出并输出，同时指针指向当前节点的右子树
}else{
p = s.top();
s.pop();
cout<<p->data<<" ";
p = p->rchild;
}
}

}

// 层次遍历，先让根入队，然后弹出并输出并依次让左右孩子入队
void AVL_Tree::Level_Traverse(AvlNode *T){
queue<AvlNode *> q;
AvlNode *p = T;
q.push(p);
while(!q.empty()){
p = q.front();
q.pop();
cout<<p->data<<" ";
if(p->lchild){
q.push(p->lchild);
}
if(p->rchild){
q.push(p->rchild);
}

}
}

// 用p带回查找到的顶点的地址,f带回p的双亲结点
bool AVL_Tree::Search_Avl(AvlNode *T,int num,AvlNode *&f,AvlNode *&p){

p = T;
while(p){
if(p->data == num){
return true;
}
if(p->data > num){

f = p;
p = p->lchild;

}else{
f = p;
p = p->rchild;

}

}
return false;

}

void AVL_Tree::Delete_AVL(AvlNode *&T,int num){

AvlNode *father = NULL;
AvlNode *p = NULL;
AvlNode *q = NULL;
AvlNode *s = NULL;

if(Search_Avl(T,num,father,p)){

if(p->lchild && p->rchild){

q = p;
s = p->lchild;
// 查找要删除节点的中序遍历的直接前驱节点
while(s->rchild){
q = s;
s = s->rchild;

}
// 直接值覆盖
p->data = s->data;

// q后移了，即p的左孩子的右子树存在
if(q != p){
// q节点的右子树高度减一，孤立了s节点
q->rchild = s->lchild;

switch(q->bf){

//删除前右子树高，现在就变成一样高
case RH:
q->bf = EH;
break;

//删除前等高，现在就变成左子树比右子树高
case EH:
q->bf = LH;
break;

case LH:
q->bf = EH;
Left_Balance(q);
break;

}
// q的左孩子的右子树不存在
}else{
// 孤立了s节点
q->lchild = s->lchild;

switch(q->bf){

case LH:
q->bf = EH;
break;
case EH:
q->bf = RH;
break;

case RH:
q->bf = EH;
Right_Balance(q);
break;
}

}
delete s;
cout<<"删除成功！"<<endl;
return;
}else{
if(!p->lchild){
q = p;
p = p->rchild;

}else{
q = p;
p = p->lchild;

}

if(!T){
T->bf = EH;
T = p;

}else if(q == father->lchild){
// 孤立了q节点
father->lchild = p;
switch(father->bf){
case LH:
father->bf = EH;
break;
case EH:
father->bf = RH;
break;
case RH:
father->bf = EH;
Right_Balance(father);
break;
}
}else{
// 孤立了q节点
father->rchild = p;
switch(father->bf){
case RH:
father->bf = EH;
break;
case EH:
father->bf = LH;
break;
case LH:
father->bf = EH;
Left_Balance(father);
break;
}

}
delete q;
cout<<"删除节点成功"<<endl;
return;

}

}else{
cout<<"要删除的节点不存在."<<endl;
return;
}
}</span>

main.app 文件

#include <iostream>
#include "Tree.h"
using namespace std;
int main(){
AVL_Tree tree;
int num=0,command;
AvlNode *root = NULL;
bool taller = false;
cout<<"___建立平衡二叉树___"<<endl;
tree.Create_AVI(root);
AvlNode *f = NULL;
AvlNode *p = NULL;

cout<<"------------------------------------"<<endl;
cout<<"1 中序遍历"<<endl;
cout<<"2 层次遍历"<<endl;
cout<<"3 查找结点"<<endl;
cout<<"4 删除结点"<<endl;
cout<<"5 插入结点"<<endl;
cout<<"-1 退出"<<endl;
cout<<"------------------------------------"<<endl;
while(cin>>command && command!= -1){

switch(command){

case 1:
cout<<"中序遍历："<<endl;
tree.InOrder_Traverse(root);
cout<<endl;
break;
case 2:
cout<<"层次遍历："<<endl;
tree.Level_Traverse(root);
cout<<endl;
break;
case 3:
cout<<"输入你要搜索的节点的值："<<endl;
cin>>num;
if(tree.Search_Avl(root,num,f,p)){
cout<<"查找得到的结果为:"<<tree.Get_data(p)<<"的地址为:"<<p<<endl;
if(f == NULL){
cout<<"因为节点"<<tree.Get_data(p)<<"是根结点，所以没有双亲结点"<<endl;
}else{
cout<<"该节点的双亲结点的值为"<<tree.Get_data(f)<<endl;
}
}else{
cout<<"查找的结点不存在"<<endl;
}
break;
case 4:
cout<<"输入要删除结点的值:"<<endl;
cin>>num;
tree.Delete_AVL(root,num);
break;
case 5:

cout<<"输入你要插入结点的值"<<endl;
cin>>num;
tree.Insert_Avl(root,num,taller);
break;

}

}

return 0;
}

建立含有元素 16 3 7 11 9 26 18 14 15 的平衡二叉树的过程如下所示：