求最长回文串的几种方法

1. 暴力法

先求出每个子串，然后再判断这个子串是不是回文串

求出每个子串的复杂度数O(N2)，判断一个子串是不是回文串的复杂度是O(N)，所以这个算法的复杂度就是O(N3)

#include <bits/stdc++.h>
using namespace std;
const int MAX = 100001;
char str[MAX];
int len;
int fun(){
int ans = 0, i, j, k;
for (i = 0; i < len; i++){
for (j = i; j < len; j++){
for (k = 0; k*2 < j-i+1; k++){
if (str[i+k] != str[j-k]){
break;
}
}
if (k*2 >= j-i+1){
ans = max(ans, j-i+1);
}
}
}
return ans;
}
int main()
{
scanf("%s", str);
len = strlen(str);
printf("%d", fun());
return 0;
}

2. 动态规划

令p[i][j]表示以i开始，以j结束的回文串的长度，如果不是回文串，p[i][j]就是0

如果p[i][j] 是一个回文串，p[i+1][j-1]也是一个回文串

首先p[i][i]是长度为1的回文串，然后状态转移方程是

if(str[i] == str[j]){
p[i][j] = p[i+1][j-1]+2;
}

算法是时间复杂度是O(N2)，所需要的空间复杂度也是O(N2)

#include <bits/stdc++.h>
using namespace std;
const int MAX = 1001;
char str[MAX];
int len, p[MAX][MAX];
int fun(){
int ans = 1, i, j, k;
memset(p, 0, sizeof(p));
for (i = 0; i < len; i++){
p[i][i] = 1;
}
for (i = len-1; i >= 0; i--){
for (j = i+1; j < len; j++){
if(str[i] == str[j]){
p[i][j] = p[i+1][j-1]+2;
}
ans = max(ans, p[i][j]);
}
}
return ans;
}
int main()
{
freopen("1.txt", "r", stdin);
while(~scanf("%s", str)){
len = strlen(str);
printf("%d\n", fun());
}
return 0;
}  

3. Manacher算法

大家都知道，求回文串时需要判断其奇偶性，也就是求aba 和abba 的算法略有差距。然而，这个算法做了一个简单的处理，很巧妙地把奇数长度回文串与偶数长度回文串统一考虑，也就是在每个相邻的字符之间插入一个分隔符，串的首尾也要加，当然这个分隔符不能再原串中出现，一般可以用‘#’或者‘$’等字符。例如：

原串：abaab

新串：#a#b#a#a#b#

这样一来，原来的奇数长度回文串还是奇数长度，偶数长度的也变成以‘#’为中心奇数回文串了。

接下来就是算法的中心思想，用一个辅助数组P 记录以每个字符为中心的最长回文半径，也就是P[i]记录以Str[i]字符为中心的最长回文串半径。P[i]最小为1，此时回文串为Str[i]本身。

我们可以对上述例子写出其P 数组，如下

新串： # a # b # a # a # b #

P[] : 1 2 1 4 1 2 5 2 1 2 1

我们可以证明P[i]-1 就是以Str[i]为中心的回文串在原串当中的长度。

证明：

1、显然L=2*P[i]-1 即为新串中以Str[i]为中心最长回文串长度。

2、以Str[i]为中心的回文串一定是以#开头和结尾的，例如“#b#b#”或“#b#a#b#”所以L 减去最前或者最后的‘#’字符就是原串中长度 的二倍，即原串长度为(L-1)/2，化简的P[i]-1。得证。 依次从前往后求得P 数组就可以了，这里用到了DP(动态规划)的思想， 也就是求P[i] 的时候，前面的P[]值已经得到了，我们利用回文串的特殊性质可以进行一个大大的优化。

核心代码

for (i = 0; i < l; i++){
if (maxpos > i){
p[i] = min(p[2*pos-i], maxpos-i);
}else{
p[i] = 1;
}
while(s[i+p[i]] == s[i-p[i]]){
p[i]++;
}
if (p[i]+i > maxpos){
maxpos = p[i]+i;
pos = i;
}
ret = max(ret, p[i]);
}

为了防止求P[i]向两边扩展时可能数组越界，我们需要在数组最前面和最后面加一个特殊字符，令P[0]=‘$’最后位置默认为‘\0’不需要特殊处理。此外，我们用Maxpos 变量记录在求i 之前的回文串中，延伸至最右端的位置，同时用pos 记录取这个Maxpos 的pos 值。通过下面这句话，算法避免了很多没必要的重复匹配。

if (maxpos > i){
p[i] = min(p[2*pos-i], maxpos-i);
}

那么这句话是怎么得来的呢，其实就是利用了回文串的对称性，如下图，



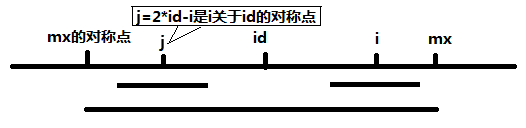
j=2*pos-1 即为i 关于pos的对称点，根据对称性，P[j]的回文串也是可以对称到i 这边的,但是如果P[j]的回文串对称过来以后超过Maxpos 的话，超出部分就不能对称过来了，如下图，



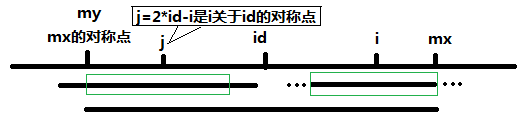
所以这里P[i]为的下限为两者中的较小者，p[i]=Min(p[2*pos-i],Maxpos-i)。算法的有效比较次数为Maxpos 次，所以说这个算法的时间复杂度为O(n)。

#include <bits/stdc++.h>
using namespace std;
const int MAX = 1001;
char str[MAX], s[2*MAX];
int p[2*MAX], l;
int Manacher(){
int i, j, pos, maxpos=0, ret = 1;
s[0] = '~';
s[1] = '#';
for (i = 0; i < l; i++){
s[2*i+2] = str[i];
s[2*i+3] = '#';
}
s[2*l+2] = 0;
l = l*2+2;
for (i = 0; i < l; i++){
if (maxpos > i){
p[i] = min(p[2*pos-i], maxpos-i);
}else{
p[i] = 1;
}
while(s[i+p[i]] == s[i-p[i]]){
p[i]++;
}
if (p[i]+i > maxpos){
maxpos = p[i]+i;
pos = i;
}
ret = max(ret, p[i]);
}
return ret-1;
}
int main()
{
freopen("1.txt", "r", stdin);
while(~scanf("%s", str)){
l = strlen(str);
printf("%d\n", Manacher());
}
return 0;
}

部分内容转自http://blog.csdn.net/yzl_rex/article/details/7908259