您的位置：首页 > 其它

百科—二分图

2016-03-29 13:25 507 查看



二分图 编辑词条

B 添加义项

?

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边(i，j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。


定义

简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集。


辨析示例

区别二分图，关键是看点集是否能分成两个独立的点集。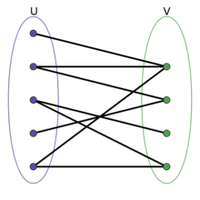



上图中U和V构造的点集所形成的循环圈不为奇数，所以是二分图。



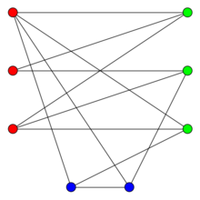
上图中U和V和W构造的点集所形成的的循环圈为奇数，所以不是二分图。


充要条件

无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。


最大匹配

求二分图最大匹配可以用最大流或者匈牙利算法。


折叠算法

求最大匹配的一种显而易见的算法是:先找出全部匹配，然后保留匹配数最多的.但是这个算法的复杂度为边数的指数级函数.因此，需要寻求一种更加高效的算法.

增广路的定义(也称增广轨或交错轨):

若P是图G中一条连通两个未匹配顶点的路径，并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径.

由增广路的定义可以推出下述三个结论:

1-P的路径长度必定为奇数，第一条边和最后一条边都不属于M.

2-P经过取反操作可以得到一个更大的匹配M'.

3-M为G的最大匹配当且仅当不存在相对于M的增广路径.

匈牙利算法

用增广路求最大匹配(称作匈牙利算法，匈牙利数学家Edmonds于1965年提出)

题目 hdoj 2063 过山车 （把这题当做二分图模板 参照一位大神详解http://blog.csdn.net/wellerzhao/article/details/7756956）
内容来自用户分享和网络整理，不保证内容的准确性，如有侵权内容，可联系管理员处理 点击这里给我发消息
标签： 
相关文章推荐
新的分享
章节导航