线性代数复习七——特征向量
2016-03-13 09:47
267 查看
定义:

为

矩阵,

为非零向量,若存在数

使

成立,则称

为

的特征值,

称为对应于

的特征向量
假设

和

是

矩阵,如果存在可逆矩阵

,使得

,则称

相似于

定理:
三角矩阵的主对角线的元素是其特征值

是

矩阵

相异的特征值,

是与

相应的特征向量,那么集合

线性无关

是可逆的当且仅当0不是

的特征值
数

是

矩阵

的特征值的充要条件是

是特征方程

的根
若

矩阵

和

是相似的,那么它们有相同的特征多项式,从而有相同的特征值(和相同的重数)

矩阵

可对角化的充分条件是

有

个线性无关的特征向量
注:
相似性和行等价不是一回事,对矩阵做行变换通常会改变矩阵的特征值
意义:
讲意义之前的一些准备工作,由于打出来不太方便,就直接拍图了,作为意义的证明(不感兴趣不需要看,直接看意义即可)


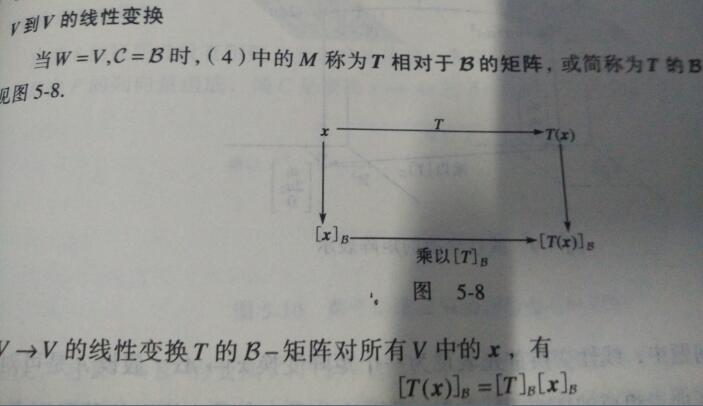


总的来说,上面的一堆图说明的就是:
你可以把矩阵

看成在我们一般选取的标准正交基下的一个变换矩阵,当然,这个矩阵可能比较复杂,可能包含旋转啊、缩放啊多种变换,但是!如果你换一个角度,选取矩阵

的特征向量作为正交基的话,那么,在这组正交基的刻画下,这个变换矩阵

只是描述了一个缩放变换,而且是在特征向量的方向上进行的放缩,其放缩的比例就是每个特征向量对应的特征值了,特征值大于1,就是放大喽,小于1,自然就是缩小了。
意义的拓展:
我们这里求的特征值,都是实数,其实,我们不妨在复数域内求解特征方程,我们自然能够得到相应的复特征值,那么这些特征值表示什么意义呢?拿简单一点的

矩阵来说吧,这里给出一个结论
设

是

实矩阵,有复特征值

及对应

中的复特征向量

,那么

,其中,

此变换为旋转和倍乘变换复合而成,逆时针旋转的角度为(0,0)到(a,b)射线的夹角,倍乘的幅值为复特征值的模。
应用这些意义,我们可以解决马尔科夫链的一些简单问题,预测未来的最终结果,应用于一些离散的动力系统,得到他们原点的属性,吸引子对应实特征值小于1(轨迹趋于0),排斥子对应实特征值大于1(轨迹远离0),鞍点对应特征值既有小于1的,也有大于1的(轨迹为马鞍形),螺线极点对应特征值为复特征值,实部为正,向外旋转,为负则向内旋转,为0的轨迹即为椭圆。
这一次的复习就到这里,下次我们继续!

为
矩阵,
为非零向量,若存在数
使
成立,则称
为
的特征值,
称为对应于
的特征向量
假设
和
是
矩阵,如果存在可逆矩阵
,使得
,则称
相似于
定理:
三角矩阵的主对角线的元素是其特征值
是
矩阵
相异的特征值,
是与
相应的特征向量,那么集合
线性无关
是可逆的当且仅当0不是
的特征值
数
是
矩阵
的特征值的充要条件是
是特征方程
的根
若
矩阵
和
是相似的,那么它们有相同的特征多项式,从而有相同的特征值(和相同的重数)
矩阵
可对角化的充分条件是
有
个线性无关的特征向量
注:
相似性和行等价不是一回事,对矩阵做行变换通常会改变矩阵的特征值
意义:
讲意义之前的一些准备工作,由于打出来不太方便,就直接拍图了,作为意义的证明(不感兴趣不需要看,直接看意义即可)





总的来说,上面的一堆图说明的就是:
你可以把矩阵
看成在我们一般选取的标准正交基下的一个变换矩阵,当然,这个矩阵可能比较复杂,可能包含旋转啊、缩放啊多种变换,但是!如果你换一个角度,选取矩阵
的特征向量作为正交基的话,那么,在这组正交基的刻画下,这个变换矩阵
只是描述了一个缩放变换,而且是在特征向量的方向上进行的放缩,其放缩的比例就是每个特征向量对应的特征值了,特征值大于1,就是放大喽,小于1,自然就是缩小了。
意义的拓展:
我们这里求的特征值,都是实数,其实,我们不妨在复数域内求解特征方程,我们自然能够得到相应的复特征值,那么这些特征值表示什么意义呢?拿简单一点的
矩阵来说吧,这里给出一个结论
设
是
实矩阵,有复特征值
及对应
中的复特征向量
,那么
,其中,
此变换为旋转和倍乘变换复合而成,逆时针旋转的角度为(0,0)到(a,b)射线的夹角,倍乘的幅值为复特征值的模。
应用这些意义,我们可以解决马尔科夫链的一些简单问题,预测未来的最终结果,应用于一些离散的动力系统,得到他们原点的属性,吸引子对应实特征值小于1(轨迹趋于0),排斥子对应实特征值大于1(轨迹远离0),鞍点对应特征值既有小于1的,也有大于1的(轨迹为马鞍形),螺线极点对应特征值为复特征值,实部为正,向外旋转,为负则向内旋转,为0的轨迹即为椭圆。
这一次的复习就到这里,下次我们继续!

相关文章推荐
- 忽视早餐,轻视生命!
- Oracle11g,在SQL Developer里新建连接时出现错误(已解决)
- eclipse下使用toolbar
- 动态规划-Number String
- 贪心+好题+Yogurt factory
- Java发送邮件的简单实现
- [国嵌攻略][141][触摸屏驱动编程]
- 堆区 栈区 方法区的区别
- Smartisan T1 的传感器全家福
- 第三周项目4-穷举法-委派任务
- Ollydbg使用技巧
- python 2.7 - 安装
- activity页面切换动画
- BestCoder Round #75 King's Game
- 学习进度第二周
- 使用GitHub pages + Hexo 快速搭建个性化博客(一)-部署Hexo默认blog模板至远程GitHub
- Windows 中 cmd 下 FTP 命令的简单使用
- 剑指offer代码分析——面试题13在O(1)内删除链表结点
- 剑指offer代码分析——面试题13在O(1)内删除链表结点
- 建立.bat文件,快速打开putty终端
