梯度下降法

设$\theta$是一个未知的参数向量，$J(\theta)$是相应的需要被最小化的代价函数。假设函数$J(\theta)$是可微的。

这个算法从最小点的初始估计值$\theta(0)$开始，之后的算法按照如下形式迭代：

$$\theta(new) = \theta(old)+\Delta\theta$$

$$\Delta\theta = -\mu\frac{\partial J(\theta)}{\partial\theta}\Bigg|_{\theta = \theta(old)}$$

该式中$\mu\gt0$。如果寻找的是最大值，那么该算法被称为梯度上升法，并去掉上式中的负号。

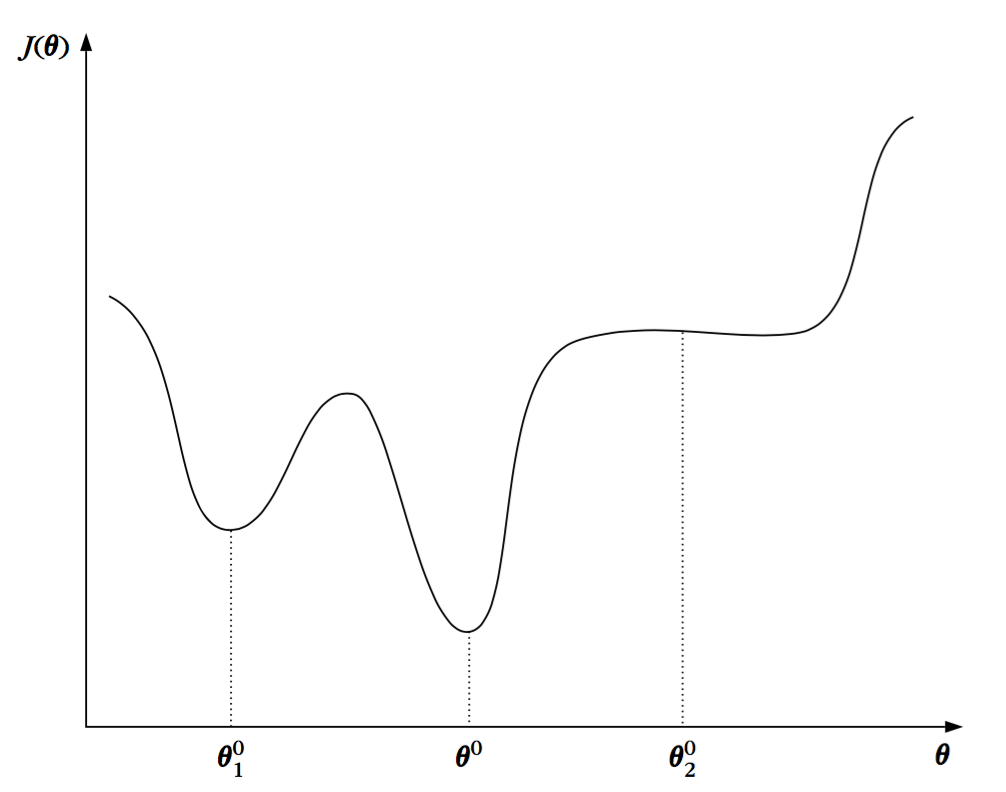
下图展示了该方法的几何解释。新的估计值$\theta(new)$是沿着减小$J(\theta)$的方向选区的。参数$\mu$是非常重要的，并且在算法的收敛中扮演了重要的额角色。如果它很小的话，那么修正值$\Delta\theta$也很小，并且收敛到最小值点就变得非常缓慢。另一方面，如果它很大的话，那么算法可能会在最优值附近震荡，也不可能收敛。然而，如果这个参数选取合适，那么算法将会收敛到$J(\theta)$的一个驻点，该驻点可以是一个局部最小值（${\theta}_1^0$）或者一个全局最小值（${\theta}^0$）或者一个鞍点（${\theta}_2^0$）。



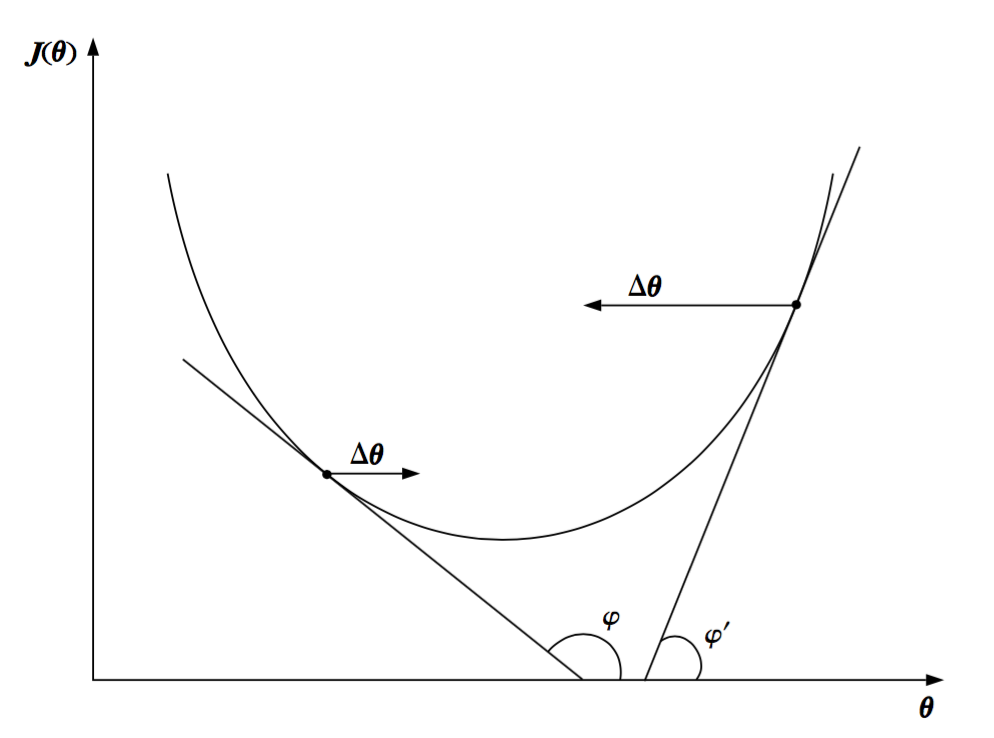
换句话说，它收敛到梯度等于0的一个点，如下图所示。算法将要收敛到哪一个驻点依赖于初始点的位置。此外，收敛的速度依赖于代价函数$J(\theta)$的形式。



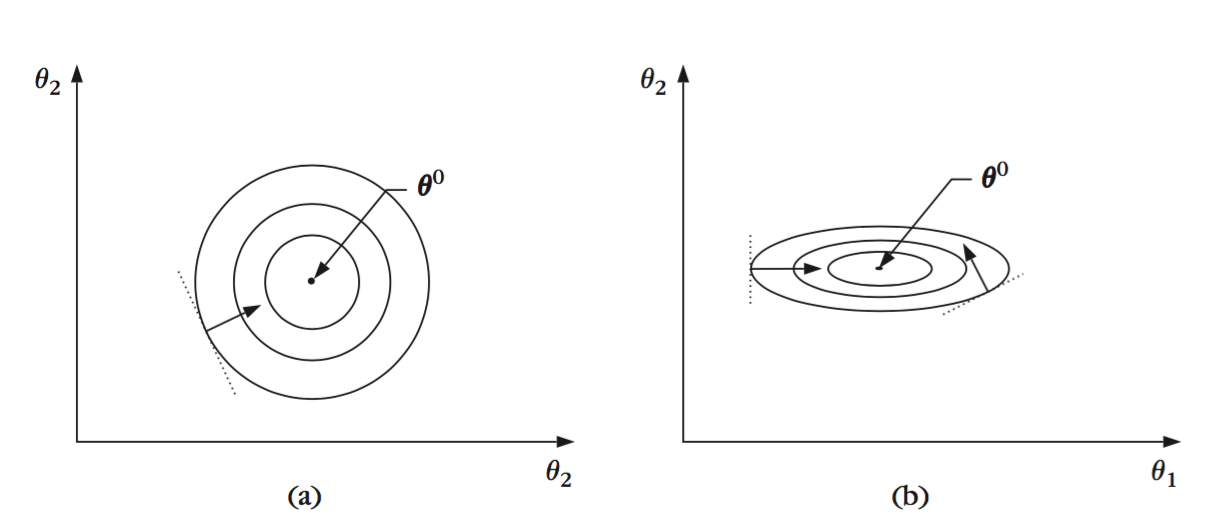
下图展示了两种情形下不同值c的等高线$J(\theta) = c$，维度是二维空间，即$\theta = [\theta_1,\theta_2]^T$。最优值$\theta^0$落在等高线的中心，梯度$\frac{\partial J(\theta)}{\partial \theta}$总是垂直于等值面的切平面。



事实上，如果$J(\theta) = c$，那么

$${\rm d}c = 0 = \frac{\partial J(\theta)^T}{\partial \theta}{\rm d}\theta \Longrightarrow \frac{J(\theta)}{\partial \theta}\perp {\rm d}\theta$$