Wunder Fund Round 2016 (Div. 1 + Div. 2 combined) 618C Constellation(计算几何+stl)
2016-01-31 17:17
316 查看
C. Constellation
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Cat Noku has obtained a map of the night sky. On this map, he found a constellation with n stars numbered from 1 to n.
For each i, the i-th
star is located at coordinates (xi, yi).
No two stars are located at the same position.
In the evening Noku is going to take a look at the night sky. He would like to find three distinct stars and form a triangle. The triangle must have positive area. In addition, all other stars must lie strictly outside of this triangle. He is having trouble
finding the answer and would like your help. Your job is to find the indices of three stars that would form a triangle that satisfies all the conditions.
It is guaranteed that there is no line such that all stars lie on that line. It can be proven that if the previous condition is satisfied, there exists a solution to this problem.
Input
The first line of the input contains a single integer n (3 ≤ n ≤ 100 000).
Each of the next n lines contains two integers xi and yi ( - 109 ≤ xi, yi ≤ 109).
It is guaranteed that no two stars lie at the same point, and there does not exist a line such that all stars lie on that line.
Output
Print three distinct integers on a single line — the indices of the three points that form a triangle that satisfies the conditions stated in the problem.
If there are multiple possible answers, you may print any of them.
Sample test(s)
input
output
input
output
Note
In the first sample, we can print the three indices in any order.
In the second sample, we have the following picture.
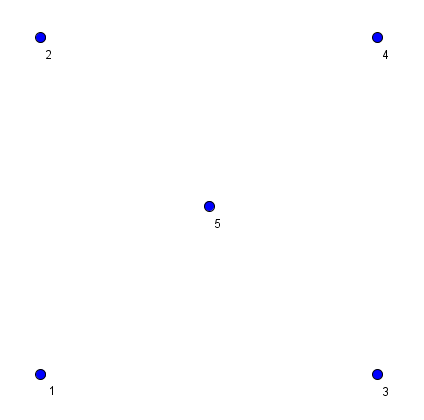
Note that the triangle formed by starts 1, 4 and 3 doesn't
satisfy the conditions stated in the problem, as point 5 is not strictly outside of this triangle (it lies on it's border).
题目链接:点击打开链接
给出n个点的坐标, 输出三个点的序号, 使得其他点都在这三个点组成的三角形的外边.
按照横坐标由小到大进行排序, 横坐标相同的则纵坐标由小到大排序, 从第三个点开始遍历, 如果三点不同线则当前三个点是所求点, 同
事也可以按照纵坐标由小到大排序, 一样的道理.
AC代码:
#include "iostream"
#include "cstdio"
#include "cstring"
#include "algorithm"
#include "queue"
#include "stack"
#include "cmath"
#include "utility"
#include "map"
#include "set"
#include "vector"
#include "list"
#include "string"
#include "cstdlib"
using namespace std;
typedef long long ll;
#define X first
#define Y second
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e5 + 5;
int n, ans;
pair<pair<int, int>, int > a[MAXN];
int main(int argc, char const *argv[])
{
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%d%d", &a[i].X.X, &a[i].X.Y);
a[i].Y = i;
}
sort(a + 1, a + 1 + n);
double k1 = double(a[2].X.X - a[1].X.X) / double(a[2].X.Y - a[1].X.Y);
for(int i = 3; i <= n; ++i) {
double k2 = double(a[i].X.X - a[2].X.X) / double(a[i].X.Y - a[2].X.Y);
if(a[i].X > a[2].X && k1 != k2) {
ans = i;
break;
}
}
printf("%d %d %d\n", a[1].Y, a[2].Y, a[ans].Y);
return 0;
}
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Cat Noku has obtained a map of the night sky. On this map, he found a constellation with n stars numbered from 1 to n.
For each i, the i-th
star is located at coordinates (xi, yi).
No two stars are located at the same position.
In the evening Noku is going to take a look at the night sky. He would like to find three distinct stars and form a triangle. The triangle must have positive area. In addition, all other stars must lie strictly outside of this triangle. He is having trouble
finding the answer and would like your help. Your job is to find the indices of three stars that would form a triangle that satisfies all the conditions.
It is guaranteed that there is no line such that all stars lie on that line. It can be proven that if the previous condition is satisfied, there exists a solution to this problem.
Input
The first line of the input contains a single integer n (3 ≤ n ≤ 100 000).
Each of the next n lines contains two integers xi and yi ( - 109 ≤ xi, yi ≤ 109).
It is guaranteed that no two stars lie at the same point, and there does not exist a line such that all stars lie on that line.
Output
Print three distinct integers on a single line — the indices of the three points that form a triangle that satisfies the conditions stated in the problem.
If there are multiple possible answers, you may print any of them.
Sample test(s)
input
3 0 1 1 0 1 1
output
1 2 3
input
5 0 0 0 2 2 0 2 2 1 1
output
1 3 5
Note
In the first sample, we can print the three indices in any order.
In the second sample, we have the following picture.

Note that the triangle formed by starts 1, 4 and 3 doesn't
satisfy the conditions stated in the problem, as point 5 is not strictly outside of this triangle (it lies on it's border).
题目链接:点击打开链接
给出n个点的坐标, 输出三个点的序号, 使得其他点都在这三个点组成的三角形的外边.
按照横坐标由小到大进行排序, 横坐标相同的则纵坐标由小到大排序, 从第三个点开始遍历, 如果三点不同线则当前三个点是所求点, 同
事也可以按照纵坐标由小到大排序, 一样的道理.
AC代码:
#include "iostream"
#include "cstdio"
#include "cstring"
#include "algorithm"
#include "queue"
#include "stack"
#include "cmath"
#include "utility"
#include "map"
#include "set"
#include "vector"
#include "list"
#include "string"
#include "cstdlib"
using namespace std;
typedef long long ll;
#define X first
#define Y second
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e5 + 5;
int n, ans;
pair<pair<int, int>, int > a[MAXN];
int main(int argc, char const *argv[])
{
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%d%d", &a[i].X.X, &a[i].X.Y);
a[i].Y = i;
}
sort(a + 1, a + 1 + n);
double k1 = double(a[2].X.X - a[1].X.X) / double(a[2].X.Y - a[1].X.Y);
for(int i = 3; i <= n; ++i) {
double k2 = double(a[i].X.X - a[2].X.X) / double(a[i].X.Y - a[2].X.Y);
if(a[i].X > a[2].X && k1 != k2) {
ans = i;
break;
}
}
printf("%d %d %d\n", a[1].Y, a[2].Y, a[ans].Y);
return 0;
}
相关文章推荐
- php 循环列找关联字段问题
- lightoj 1403 - Air Raid
- git常用命令学习笔记
- 【CSS】盒子模型 之 IE 与W3C的盒子模型对比
- Linux下Mysql简单操作
- Android AttributeSet
- CentOS6.5下Git服务器搭建
- git命令大全
- Git命令参数及用法详解(转)(二)
- Git命令参数及用法详解(转)(一)
- linux下删除指定文件之外的其他文…
- org.hibernate.MappingException: could not instantiate id generator
- thinkphp嵌套层数分析(转)
- 键盘事件keydown,keypress,keyup区…
- WindowsServer 2008 iis+php配置
- 域名解析的记录类型:A记录、CNAME…
- ecshop添加新的配送方式(转)
- php缓存技术总结(转)(二)
- php缓存技术总结(转)(-)
- 移动搜索SEO分享:利用Meta声明来…
