标量对矩阵求导
2015-10-06 20:55
1136 查看
网上的求导没有涉及到链式法则,稍微一复杂点我就不知道每个因式是否应该转秩,是放在左边还是右边。。。
而且标量对矩阵求导在博客上怎么也没找到,(找到的麻烦告诉我一声),最后在wiki上找到了。
看了半天,觉得Wiki上写的最全面,于是把里面最万能的精华部分拿了出来。
有了这几个公式,相信无论遇到多复杂的式子,只要结果能表示成矩阵,就肯定能轻松求出来了。首先翻译一下文章大意:
矩阵分析(求导)所用的符号主要分成了两大流派:最明显的区别在于当对标量求关于向量的导数时,结果到底是行向量还是列向量
张量(上下标)记号一般在物理里面用的多。
然后讲了标量、向量、矩阵互相求导的公式,具体的在此略过。
然后,重点来了!
如果写成微分的方式,就可以不用记那么多的公式了。
第一部分是微分的性质,第二部分是如何从微分转化为求导。
注意:
对矩阵求导是没有链式法则的!!!
注:wiki上好像没有求逆矩阵的微分公式,在此补上
d( X^(-1) ) = - X^(-1)*dX*X^(-1);
以下转载自wikipedia:地址:https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-matrix_identities
Identities in differential form[edit]
It is often easier to work in differential form and then convert back to normal derivatives. This only works well using the numerator layout. In these rules, "a" is a scalar.| Condition | Expression | Result (numerator layout) |
|---|---|---|
 | 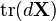 | |
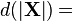 | 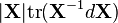 | |
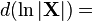 |  |
| Condition | Expression | Result (numerator layout) |
|---|---|---|
| A is not a function of X | 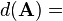 |  |
| a is not a function of X |  | 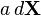 |
 |  | |
 | 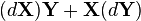 | |
| (Kronecker product) | 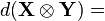 |  |
| (Hadamard product) | 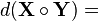 | 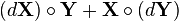 |
 |  | |
| (conjugate transpose) | 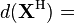 | 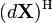 |
| Canonical differential form | Equivalent derivative form |
|---|---|
 |  |
 | 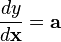 |
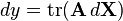 | 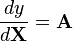 |
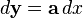 |  |
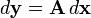 |  |
 | 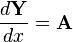 |
相关文章推荐
- 【目录】工具记录
- 如何设置centos6 不启动桌面环境gnome
- 如何设置centos6 不启动桌面环境gnome
- android手游渠道接入业务+技术全讲解
- 前行的路
- FZU 2203 单纵大法好 (二分+贪心)
- iPhone 6s物料成本不到1500?但你知道了不照样选择剁手嘛
- 【温故而知新】【3】时钟分频-半整数分频N.5
- 关于mysql_affected_rows()
- 软件工程之程序编码
- 【转】不要学习代码,要学会思考
- 【bzoj4144】[AMPPZ2014]Petrol
- adb 命令
- 关于线程操作的waitpid()
- 面向对象的一些概念及举例说明
- C++顺序循环队列
- Foj 2203 Problem 2203 单纵大法好 stl应用
- 解决UIGestureRecognizer手势与视图上其他滑动视图的冲突
- 视图(View) – ASP.NET MVC 4 系列
- [算法运用研究]局部标准差实现对比度增强
